Zanim pokażę receptę na tzw. bieda-emerytury, przypomnę, że zgodnie z ustawą o rentach i emeryturach zarówno składki na emeryturę jak i same emerytury są waloryzowane o inflację. Składki są dodatkowo waloryzowane o 100% wzrostu realnego PKB, a same emerytury co najmniej o 20% tego wzrostu. Komuś może się nie podobać to 20%, ale trzeba pamiętać, że emeryt ponosi mniejsze koszty niż pracujący (choćby na dojazdy do pracy i w ogóle ma czas wolny). Jeżeli więc dziś emeryci nie umierają z głodu, to twierdzenie, że w przyszłości będą umierać albo przymierać głodem jest po prostu fałszem. Sama waloryzacja o inflację sprawia, że koszty życia nie mogą rosnąć, musi być tak samo jak wcześniej. Biorąc pod uwagę dodatkowy bodziec gospodarczy może być tylko lepiej.
W takim razie pytanie czy takie oto teksty, jak Nationale-Nederlanden można uznać za poważne: Stopa zastąpienia - dzięki niej zobaczysz swoją biedę Emerytura
Jeśli uważasz, że obecni emeryci otrzymują niskie świadczenia, to jesteś w błędzie. Ich emerytury są bardzo przyzwoite w porównaniu do tego, ile Ty dostaniesz. Przerażający scenariusz? To będzie Twoja rzeczywistość – otrzymasz jedynie 25-40 proc. swojej ostatniej pensji.
Zaczęło się od trzęsienia ziemi, to napięcie musi rosnąć:
Dokonajmy małego eksperymentu. Zobaczmy, jak zmieniać się będzie wysokość emerytur w przyszłości. Za punkt wyjścia przyjmiemy obecną średnią płacę. Ta będzie oczywiście rosła, ale też będą drożeć towary. Miejmy nadzieję, że zarobki będą rosły szybciej niż inflacja, jednak teraz na potrzeby eksperymentu załóżmy, że jej realna wartość pozostanie bez zmian. Nominalnie będzie dużo wyższa, ale kupimy za nią tyle samo dóbr, co dziś.
Jak przeżyć za 1,5 tys. zł?
Do pokazania, jak będą zmieniać się emerytury, używamy prognozy stopy zastąpienia przygotowanej przez ZUS. Stopa zastąpienia to relacja przeciętnej emerytury do przeciętnej pensji. Obecnie wynosi ona 56,4 proc. Zatem osoba zarabiająca dziś średnią krajową w wysokości 5,2 tys. zł, otrzyma jutro emeryturę w wysokości 2,9 tys. zł.
Jeszcze nie najgorzej, prawda? Załóżmy jednak, że na emeryturę przechodzisz za 10 lat. Wtedy stopa zastąpienia wyniesie 47,1 proc., zatem emerytura będzie w wysokości 2 450 zł.
Emeryci, którzy skończą pracę za 20 lat, będą dostawać 1 950 zł. To już trochę gorzej wygląda. Mniej niż pensja minimalna. Dałbyś radę za tyle przeżyć?
To nie koniec. Za 30 lat emeryci otrzymywać będą 28,7 proc. swoich dotychczasowych zarobków. Gdyby taka stopa zastąpienia była dziś, emerytura byłaby w wysokości… 1,5 tys. zł.
Gdyby tylko ubezpieczyciele pisali takie rzeczy, to uznałbym to za zwykłą reklamę swoich produktów, manipulującą faktami. Jednak w podobnym tonie piszą wszędzie w mediach, więc trzeba na to spojrzeć nieco poważniej. Wydaje mi się, że za ten stan rzeczy w dużym stopniu odpowiadają instytucje. Np. wg Komisji Europejskiej zagrożenie ubóstwem ma miejsce, gdy dochód wynosi poniżej 60% mediany dochodu w danym państwie (Komisja Europejska, Adekwatność i Stabilność Świadczeń Emerytalnych).
Wydawało mi się, że zagrożenie ubóstwem to jest wtedy, gdy ledwo stać na utrzymanie, bo to chyba powinien być punkt odniesienia. A tu się okazuje, że jak nie stać mnie na 3 telewizory, tylko na 2, a większość stać na 3, to jestem biedakiem. Jeśli już, to powinno się odróżnić ubóstwo względne od absolutnego. Chociaż i tutaj słowo "ubóstwo" mi nie pasuje.
To wróćmy do analizy biedaemerytur. Wysokość emerytury uzyskujemy w postaci sumy zwaloryzowanych (o nominalny wzrost przeciętnych wynagrodzeń) składek podzielonych przez tzw. dalsze trwanie życia (ponad 200 miesięcy). Powiedzmy, że nie ma wzrostu PKB. Np.
6000 zł [pensja]*19,52% [składka] *12 [m-cy]*30 [lat] / 200 [m-cy] = 2108.
Jeśli żyjemy dłużej o rok (212 mcy):
6000 *19,52% *12 * 30 / 212 = 1989 zł.
Jeżeli o 2 lata - 1882 zł. O 5 lat - 1622.
Pozornie wydaje się, że ubezpieczyciel ma rację i niepotrzebnie się go czepiam. Mało kto zauważa jednak, że waloryzacja jest powiązana z dalszym trwaniem życia. Wyższy PKB podnosi długość życia - nie można tych dwu aspektów traktować jako zmienne niezależne. Zobaczmy do czego to prowadzi:
Więcej zarabiamy -> jakość naszego życia jest wyższa -> żyjemy dłużej
Ale z drugiej strony:
Więcej zarabiamy -> nasze składki są wyższe oraz waloryzowane -> nasza emerytura jest wyższa
Załóżmy, że długość życia rośnie proporcjonalnie do składek. Jeżeli większą składkę podzielimy przez większy okres dalszego życia, to emerytura może pozostać taka sama! Wniosek? W przykładzie ubezpieczyciela błędne jest założenie, że PKB nie rośnie i w ten sposób zaniża on emeryturę z ZUSu. Aby zrównoważyć dłuższe trwanie życia ze wzrostem PKB, to w moim przykładzie, gdy żyjemy dłużej o rok, 6000 (albo składkę) muszę pomnożyć przez 2108 / 1989 = 1,06: 6000 zł * 1,06 *19,52% *12 *30 / 212 = 2108. Emerytura się nie zmieniła.
W rzeczywistości te 6% to zdecydowanie za dużo. Poniżej na podstawie GUSu zrobiłem wykres dalszego trwania życia w latach - średnioważone dla kobiet i mężczyzn (waga dla mężczyzn: 0,42 - wg GUS w 2020 mężczyźni od 60 r. życia stanowili 42% osób od 60 r. ż.) wraz z linią trendu, od 1995 do 2020:
Źródło: obliczenia własne na podst. GUS. Waga dla mężczyzn: 0,42.
Załamanie trendu w 2020 psuje cały obraz, ale można przypuszczać, że nastąpi powrót. Średnio wychodzi, że długość życia rośnie co roku o ok. 0,14 roku, choć gdyby usunąć ostatni rok, dostalibyśmy 0,156. Teraz wynik jest sensowny: PKB realnie rośnie o 3-5% i przekłada się to na 0,14-0,16 dodatkowego roku dalszego życia - czyli co roku żyjemy dłużej o ok. 2 miesiące . A to znaczy, że w moim przykładzie za wzrost 6% trzeba wstawić 4% (średnia z 3 i 5% wzrostu PKB), a za 212 należy wstawić 202:
6000 * 1,04 * 19,52% *12 *30 / 202 = 2171. Nasza emerytura wzrosła o 3% (tzn. 2171 / 2108 = 1,03).
Stopa zastąpienia spada
Stopa zastąpienia to przeciętna emerytura podzielona przez średnią płacę w gospodarce. Skoro wiemy, że PKB (wynagrodzenia) mają rosnąć o ok. 4%, a emerytura o 3%, to jasne się staje, dlaczego stopa zastąpienia spada! Dla naszego przykładu
Rok 1 emerytury: stopa zastąpienia = 2108 / 6000 = 35,13%
Rok 2 emerytury: stopa zastąpienia = 2108*1,03 / (6000*1,04) = 2171 / 6240 = 35%
Rok 3 emerytury: stopa zastąpienia = 2108*1,03^2 / (6000*1,04)^2 = 34,46%
...
Rok 10: 2751 / 8539,9 = 32%
Rok 20: 3697 / 12641 = 29%
Rok 30: 4968 / 18712 = 26,5%
Widzimy więc, że stopa zastąpienia spada, bo (realne) wynagrodzenia rosną o ok. 1 pkt proc. więcej niż emerytury. Ktoś mógłby zarzucić temu modelowi, że zakłada ciągle wzrost długości trwania dalszego życia, co wcale nie jest takie oczywiste i ostatni rok to udowodnił. Oczywiście to prawda, ale pamiętajmy, że zakładamy tu co roku 2 miesiące dodatkowego życia, co w perspektywie 10 lat daje 1,67 wzrostu trwania życia, 20 lat - ponad 3 lat i 30 lat - 5 lat. Dziś średni wiek życia to 77-78, więc dodanie 5 lat jest jak najbardziej realne biorąc pod uwagę, że we Francji, Szwecji, Hiszpanii i wielu innych krajach jest to 83 (por. tutaj).
Rozumiemy więc już, że cały wrzask o bieda-emerytury to pic na wodę fotomontaż, który ma tylko na celu naganiać na dodatkowe ubezpieczenia i ofe. Oczywiście media na tym dodatkowo żerują, bo to dla nich chwytliwy temat.
W każdym razie, już wiemy, którego ubezpieczyciela i OFE unikać.
Jak jest w innych krajach?
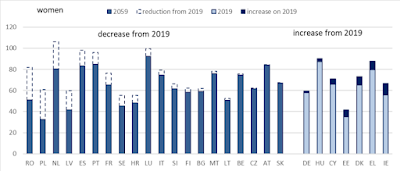
Szczegółową analizę stopy zastąpienia krajów UE znalazłem w Pension adequacy report 2021. W większości przypadków prognozuje się spadek stopy zastąpienia, KE porównuje 2019 z 2059. Dla kobiet:
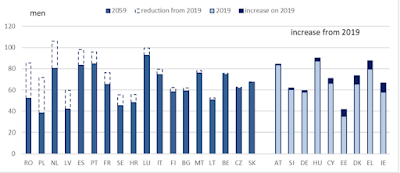
Dla mężczyzn:
Źródło: KE, 2021 pension adequacy report, s. 69
Źródło: ibidem, s. 150.
Rzeczywiście Polska na tle pozostałych krajów wygląda kiepsko, skoro w 2059 prognozuje się najniższy poziom stopy zastąpienia ze wszystkich krajów UE. Jedynie Estonia i Łotwa mają mieć zbliżony do naszego. Z czego to wynika? Z pewnością ma to związek z niskim wiekiem emerytalnym kobiet.
Zaniżony wiek emerytalny kobiet
Z niezrozumiałego powodu kobiety mają prawo do emerytury o 5 lat wcześniej od mężczyzn mimo że przeciętnie o 5 lat dłużej żyją. W obecnych czasach jest to całkowicie nieracjonalne. Z tego powodu najwyraźniej ta nieracjonalność przebija się do statystyki. Tę intuicję wspiera porównanie wieku emerytalnego kobiet w krajach Unii. W tym samym raporcie KE znajdziemy podział tego wieku w 2019 oraz prognozowanym w 2059 (z tego samego raportu):
Źródło: ibidem, s. 72.
I co się okazuje: jesteśmy jedynym z tej listy krajem, dla którego szacuje się, że w 2059 wiek emerytalny kobiet pozostanie na poziomie 60 lat. Wszyscy dobrze wiemy, że tak nie będzie. Wszystkie pozostałe kraje mają podwyższony wiek do 65 lub więcej i u nas też tak się stanie.
Dlaczego KE tylko u nas nie podwyższyła tego wieku? Statystycy, którzy opracowują ten raport, współpracują z władzami danego kraju; to urzędnicy państwowi musieli się uprzeć na te 60 lat wbrew logice. Krótko mówiąc - raport ma podłoże polityczne i nie można go traktować jako całkowicie obiektywne źródło informacji. Oczywiście stopa zastąpienia będzie zbliżona do średniej innych krajów, jeśli tylko nastąpi urealnienie wieku przejścia na emeryturę u kobiet.
Trzy sposoby na "bieda-emerytury"
Czy można zrobić coś, co podniesie stopę zastąpienia, tak aby przyszłym emerytom żyło się nieco lepiej w stosunku do prognoz? Oczywiście mówimy tu o sposobach, które nie obciążą dodatkowo systemu. Jedno rozwiązanie już podałem. Należy wprowadzić równouprawnienie kobiet i mężczyzn poprzez zrównanie ich wieku emerytalnego. U naszych zachodnich sąsiadów istotnie ten wiek jest taki sam (do roboty lewica). De facto kobiety powinny przechodzić nawet później na emeryturę, skoro statystycznie żyją dłużej o ok. 5 lat, ale to już kwestia bardziej dyskusyjna.
Wg R. Gwiazdowskiego podwyższenie wieku nawet do 67 lat dla obu płci, nie zlikwidowałoby dziury w systemie emerytalnym. O ile pamiętam, Gwiazdowski popierał, przynajmniej początkowo, program 500+, który nie tylko nie poprawił sytuacji demograficznej (a przecież to było głównym celem), ale pogorszył sytuację budżetu państwa. Dlatego ciężko mi Gwiazdowskiego traktować jako autorytet.
I tu dochodzimy do drugiego sposobu. Ogromna rzesza ludzi, którzy dobrze lub bardzo dobrze zarabiają, traktują 500+ jak... przyszłą emeryturę. Nie wydają tego, bo mają dość pieniędzy. Finansowanie tych osób w obliczu wielu potrzeb w kraju jest skrajnie niemoralne i nieodpowiedzialne. Tak więc te osoby czy dzieci tych osób powinny mieć obniżone emerytury o te kwoty, bo już płacimy składki czyli podatki na nie.
Tzw. eksperci od tematu widzą często tylko jedną stronę medalu - za małą dzietność, nie zwracając uwagi na przyczyny tego stanu rzeczy. Wiadomo, że główną przyczyną jest to, że ludzie częściej i dłużej poświęcają się karierze zawodowej. Jeżeli to przekłada się na wzrost PKB, to znaczy, że mamy do czynienia z jakby substytucją między populacją a PKB. Szybki tryb życia, konsumpcjonizm i kariera zawodowa mają swoją cenę. Jeżeli populacja młodych i czynnych zawodowo nie rośnie albo nawet spada przy rosnącej gospodarce, a jednocześnie liczba emerytów wzrasta, to należy zmniejszyć udział wydatków finansów publicznych związanych z niektórymi sektorami, gdzie głównym beneficjentem jest młodsza populacja.
A zatem trzecim dodatkowym sposobem jest zmniejszenie udziału finansowania policji, mediów czy kultury (w ujęciu realnym) w PKB. Ponownie, nie znaczy to obniżenie wartości wydatków, tylko przeniesienie części wzrostu gospodarczego z tych sektorów na sektor emerytalny.