Inflacja a luka PKB

Niedawno straszyłem inflacją 20% albo i więcej, bo z taką sytuacją mieliśmy do czynienia w czasach grypy hiszpanki. Trzeba jednak pamiętać, że były to czasy zakończenia I wojny św. Wprawdzie model regresji rozdzielał śmiertelność z powodu wojny od samej grypy, niemniej jakiś pośredni wpływ mógł pozostać. Poziom inflacji tak naprawdę zależy głównie od luki PKB (Output gap).

W ostatnich latach ekonomiści dyskutują na temat tego dlaczego bailouty przeprowadzone na ogromną skalę w USA w czasach kryzysu 2008-2010 i najniższe w historii stopy proc. nie wywołały ostrej inflacji. Wydumanych wytłumaczeń ekspertów przeciętny zjadacz chleba nie jest w stanie słuchać: rozmienianie się na drobne, wchodzenie w niepotrzebne szczegóły, bez prostego  zobrazowania zjawiska, jest nie do zniesienia nawet dla ludzi bardziej obeznanych z tematem. A mechanizm zawsze trzeba przedstawić od początku: cena jest wypadkową popytu i podaży, wobec czego przy stałej podaży spadek popytu powoduje spadek cen, a wzrost popytu - wzrost cen. Przy stałym popycie spadek podaży (produkcji) wywołuje wzrost ceny, a wzrost podaży - spadek ceny. Jeżeli firma ma niewiele zapasów, a popyt na towar rośnie, to jest to sytuacja gdy podaż nie może nadążyć za popytem i stąd powstaje inflacja. Gdy natomiast firma ma dużo zapasów i nie może się ich szybko pozbyć, to obniża ceny - dostajemy deflację.

A teraz sobie wyobraźmy sytuację, że firma ma dużo zapasów, obniżyła ceny, ale nadal popyt jest marny (z jakiegoś powodu nadszedł kryzys). Firma nie może dalej obniżać cen, bo przestałaby się opłacać jej działalność. Co więc robi? Zmniejsza produkcję, czyli zwalnia pracowników albo wysyła ich na bezpłatny urlop (jeśli byłoby to prawnie możliwe). W ten sposób produkcja stopniowo dostosowuje się do popytu - dochodzi do równowagi. Jednak jest to chwiejna równowaga. Skoro firma zwolniła pracowników, tym samym spowodowała, że ci pracownicy nie mają teraz pieniędzy na konsumpcję. A jak nie mają na konsumpcję, to kolejne firmy przestają na nich zarabiać i dołączają one do trudnej sytuacji tej pierwszej firmy. Ale to oznacza, że i te firmy muszą zwolnić pracowników. Ci pracownicy są jednocześnie konsumentami pierwszej firmy, co oznacza, że popyt na jej towary jeszcze bardziej spada. To oczywiście oznacza dalsze cięcia albo bankructwo... Jak widać równowaga okazała się złudzeniem, a optymalny poziom produkcji przestaje istnieć.

Recesje i boomy są samonakręcającą się spiralą. Gdy gospodarka podlega takiemu efektowi domina, to tylko naiwni, żyjący abstrakcją korwiniści pozostawiliby kraj na pastwę losu. Jednak oczekuje się, że państwo coś zrobi. I teraz zastanówmy się co się stanie, jeżeli państwo dostarczy rynkowi zastrzyk pieniędzy, np. w postaci niskooprocentowanych pożyczek czy zasiłków? Wielu błędnie zaczyna tok rozumowania od tego punktu, twierdząc, że w ten sposób państwo nakręca inflację. Nie rozumieją, że te pieniądze muszą pójść na odbudowanie produkcji, co pociągnie zatrudnienie, a więc część realną gospodarki. To nie jest druk pustego pieniądza. Dopóki gospodarka nie wróci do stanu zero, dopóty ceny nie będą rosły.

Ten stan zero wyznacza właśnie potencjalny produkt brutto. Zobaczmy jego definicję wg pwn:

Potencjalny Produkt Narodowy Brutto - poziom produktu narodowego brutto, który byłby osiągnięty w warunkach równowagi ekonomicznej, tj. bez inflacji, przy pełnym wykorzystaniu aparatu wytwórczego i siły roboczej (przy pełnym zatrudnieniu);

Ze względu na różnego rodzaju niedoskonałości (nieefektywności) rynku, ten perfekcyjny stan nie jest możliwy do osiągnięcia w praktyce. Dlatego praktyczna definicja mówi, że jest to produkcja przy naturalnej stopie bezrobocia (5-6%). Z tego wynika, że gdy bezrobocie jest poniżej naturalnego, to realny PKB jest powyżej potencjalnego PKB, a gdy bezrobocie jest powyżej naturalnego, PKB spada poniżej potencjalnego PKB.

W sumie można nawet uznać, że zbyt niskie bezrobocie wcale nie jest tak dobre dla gospodarki, jakby się wydawało. Bo to oznacza, że wszyscy konsumują na potęgę, a nasza firma może nie wyrabiać z produkcją i musi podnieść ceny. Tak rodzi się inflacja.

Ktoś zapyta: skoro firma nie wyrabia i podnosi ceny, to gdzie tu nadprodukcja postulowana przez teorię potencjalnego PKB? Trzeba znów przypomnieć co rozumiemy przez nadprodukcję. Niestety mamy tu problem już z nazewnictwem: czy chodzi o produkcję czy o konsumpcję. Klasycznie PKB to produkcja (podaż) równa popytowi. Ale popytowi na co? Na towary i usługi. Czyli popyt na dobra i usługi jest równy podaży na nie. Ale z punktu widzenia podaży (producenta) mamy jeszcze rynek pracy, w którym występuje popyt na pracę (szukanie pracowników) i podaż pracy (szukanie pracy przez ludzi), a ceną jest wynagrodzenie. Na tym rynku także musi dojść do równowagi. I teraz, żeby rozjaśnić powyższą kwestię nadprodukcji. Nadprodukcja nie oznacza tutaj nadwyżki podaży nad popytem na towary, bo to przecież rodziłoby deflację. Jest na odwrót. Popyt wyprzedza podaż. Nasza nadprodukcja stanowi nadwyżkę popytu (na dobra, usługi oraz pracę) nad podażą (dóbr, usług, pracy). Innymi słowy oznacza jedynie taki poziom produkcji, że firma ma trudności ze znalezieniem nowych pracowników lub zatrzymaniem starych. Musi więc ich przyciągnąć podwyżkami płac. Wzrost wynagrodzenia staje się następnym źródłem inflacji.

Luka PKB to różnica między realnym PKB a potencjalnym PKB. Ponieważ ten drugi jest konstruktem teoretycznym, to są różne metody jego oszacowania i przez to interpretacja skonstruowanej luki staje się empirycznie kontrowersyjna. Z teoretycznego punktu widzenia powinna istnieć silna korelacja między luką a inflacją. Większa luka oznacza większą inflację. Aby luka stała się praktycznym narzędziem do prognoz inflacji, musi istnieć taka korelacja.

OECD ma własną metodologię szacowania luki PKB. Na ich stronie znajdziemy statystyki dla wielu krajów. Z kolei na tej stronie organizacja publikuje roczne stopy inflacji (CPI). Zatem możemy sprawdzić czy rzeczywiście luka koreluje z inflacją. Pobrałem dane dla lat 1999-2019. Oto wyniki korelacji Pearsona dla tych krajów:

Dla kraów OECD korelacja równa się ponad 64%, czyli dużo. Jednakże różnice są skrajne: dla Grecji wynosi aż 78%, USA wynosi 61%, dla Polski tylko 2,2%, dla UK -12,4%, dla Słowacji -20%. Dlatego wcześniej zwróciłem uwagę na problem konstrukcji luki, który może dawać różne rezultaty dla różnych krajów. Za chwilę się nad tym zastanowimy.

Popatrzmy na USA:

Źródło: OECD

Średnia arytmetyczna luki w tym okresie = -1,356%. Średnia inflacja = 2,17%. O czym to świadczy? Że mimo ujemności luki inflacja w USA pozostała dodatnia. Są więc jeszcze inne stałe czynniki kreujące inflację, będące najprawdopodobniej konsekwencją innych interwencjonistycznych działań rządu, jak wzrost pensji minimalnej. To dlatego powstaje niekiedy "paradoksalny" stan zwany stagflacją, gdy bezrobocie i inflacja rosną, a PKB spada.

Dalej, zobaczmy, że FED sam złamał dotychczasową korelację w roku 2009-2010 właśnie poprzez wspomniane programy pomocowe. Gdyby FED nic nie robił, USA miałyby prawdopodobnie deflację, bo przecież wpadły w nią w 2009 i nagle odbiły. Potem inflacja zaczęła spadać, a luka się zmniejszała. Dopiero od 2017 nastąpił powrót do normalnej zależności.

Wniosek jest następujący: USA podjęły właściwe działania, chociaż kosztem BYŁA wbrew pozorom inflacja. Po prostu jej zmiana była niewidoczna na tle średniej inflacji w USA. Gdyby rząd USA nie generował inflacji dodatkowymi działaniami, to podczas ujemnej luki inflacja także byłaby ujemna.

Wróćmy do kraju. Korelacja jest u nas zaskakująco niska (2%), ale zobaczmy jak przebieg obu zmiennych wygląda historycznie:

Źródło: OECD

Widać, że jednak istnieje bardzo silny związek, którego współczynnik Pearsona nie uchwycił. Wystarczy jednak, że zamiast poziomów użyjemy zmiany kolejnych poziomów, a wtedy korelacja między luką PKB a inflacją wyniesie w Polsce aż 64%. Zmiany zawsze lepiej pokazują korelacje, bo korelacja poziomów zależy od samej metodologii  konstrukcji wskaźnika, a w przypadku zmian nie ma to znaczenia.

To co różni nasz kraj od Ameryki to dodatnia luka PKB. To właśnie ona stanowi główną przyczynę rosnącej ostatnio inflacji. USA nie musi się o nią martwić. U nas jest odwrotnie, a mimo to rząd i NBP bezmyślnie naśladuje USA i inne kraje. Przykładowo NBP obniża jeszcze bardziej stopy proc. I po co, skoro sami zakazali prowadzić działalności, czyli także inwestycji. Oczywiście ktoś na tym skorzysta, ale nie ten, kto powinien. Efektem tych działań będzie, właściwie już jest, wspomniana stagflacja.

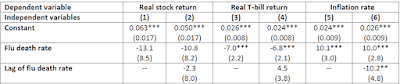
P. S. Przypominam, że stopy zwrotu rynku akcji są ujemnie skorelowane z inflacją (zob. Czy inflacja jest dobra dla akcji?). W latach 1999-2019 korelacja między nominalnymi stopami zwrotu WIG a stopą inflacji w Polsce jest lekko ujemna i wynosi -10%.

Link do arkusza z danymi znajduje się niżej:
Luka PKB vs inflacja

Kalkulator do obliczania zysków z akcji metodą FIFO

Chociaż obliczanie zysków i strat z papierów wartościowych pozornie wydaje się sprawą bardzo prostą, to dla wielu transakcji (na tym samym walorze) okazuje się to zaskakująco trudne. Dla jednej transakcji kupna i sprzedaży, zadanie jest banalne. Jednak w momencie gdy jednego dnia kupujemy 10 akcji po cenie p1, następnego dnia 30 akcji po cenie p2, a potem sprzedajemy wszystkie 40 akcji po p3, to obliczamy zysk metodą FIFO (First In, First Out) znaną księgowości, tj. pozbywamy się najpierw tych aktywów, które kupiliśmy wcześniej, a więc dostajemy 10*(p3 - p1)  i do tego dodajemy resztę, czyli 30*(p3 - p2). Sytuacja się jeszcze bardziej komplikuje, gdy papiery sprzedajemy partiami, np. 5 akcji po p3 i 35 po p4. Wtedy mamy 5*(p3 - p1) + 5*(p4 - p1) + 30*(p4 - p2).  Ręczne obliczanie dochodów staje się bardzo żmudne, a prostej funkcji w Excelu do tego nie znajdziemy.

Oczywiście są programy, które obliczają to wszystko za nas. Jednakże zwykły inwestor giełdowy ma trudniej, bo nie używa programów księgowych i najczęściej musi sam liczyć w arkuszu kalkulacyjnym. Gdy robi niewiele transakcji, to nie jest to wielki problem, ale w pewnym momencie i przy większej liczbie transakcji można się pogubić albo pomylić. Ja dotychczas nie stosowałem FIFO i to co robiłem to opierałem się na metodzie średniej ważonej ilością wolumenu. Im większa ilość danego papieru, to tym większa była waga w cenie zakupu / sprzedaży. Ta metoda dawała niezłe przybliżenie rzeczywistych wyników. Nie pozwalała jednak ocenić czy w danym roku będzie płacony PIT i w jakiej wysokości. 

Stworzyłem więc makro, które oblicza metodą FIFO dochody kapitałowe na podstawie wyciągu bankowego. Link do pobrania znajdziemy tutaj . W pliku są dwa arkusze. Dla przykładu pierwszy wygląda tak:

Mamy tu wyciąg operacji kupna i sprzedaży podobny do tego, jaki można ściągnąć w formacie .csv w eMaklerze, tj. mbanku. Z tym że w kolumnie 'Wartość' jest formuła, uwzględniająca dodatkowo prowizję. Ustawienia prowizji są w komórkach K2 (minimum 3 zł) i L2 (maksimum 0,39%). Jeśli więc nasz wyciąg zawiera już prowizję (cena kupna jest powiększona o nią, a cena sprzedaży pomniejszona), to po prostu wpisujemy 0. Jeśli chodzi o 'Czas transakcji', to musi mieć format tekstu i zawierać 4 cyfry roku, a transakcje muszą być posortowane od najnowszej do najstarszej. W mbanku podany jest dokładny czas, czyli data i godzina, co generalnie nie ma żadnego znaczenia dla tego kalkulatora, ponieważ dla niego liczy się tylko rok kupna i sprzedaży. Z tym że godzina wskazuje która transakcja była wcześniej, więc jeśli dostajemy oryginalną listę transakcji w odwrotnej kolejności, to wtedy będzie mieć znaczenie godzina dla koniecznego posortowania. Kolumna 'K/S' to oczywiście kupno/sprzedaż, natomiast kolumna 'Giełda' nie ma większego znaczenia (możemy ją użyć do jakichś dodatkowych własnych oznaczeń).

Kiedy mamy wszystko poprawnie ustawione, klikamy przycisk do obliczania zysków i strat. Może pojawić się okno z ostrzeżeniem, że liczba sprzedanych walorów nie pokrywa się z liczbą kupionych walorów. Pamiętajmy, by uwzględnić splity, resplity, pda itp. - najlepiej skorygować mniejszą liczbę akcji do większej i większą wartość do mniejszej ze względu na zaokrąglenia. Drugi arkusz przedstawia wyniki:

Tabela pokazuje zyski z każdej transakcji sprzedaży. Suma po danym roku podatkowym pokaże faktyczne dochody lub straty w tym roku.

Kalkulator będzie pomocny także do sprawdzenia, czy w otrzymanym PIT-8C dostaliśmy takie same wartości. W razie czego możemy się też nim posłużyć, jeśli zgubiliśmy PIT z dawnych lat.

Czy powinniśmy przygotować się na inflację rzędu 20%?

Polecam bardzo ciekawy artykuł A. Gaafara "Grypa hiszpanka – pandemia groźniejsza od wojny"  z kwietnia tego roku, unaoczniający podobieństwo historii pandemii grypy hiszpanki (1918-1920) do obecnego koronawirusa. Może być to wielce pouczające zarówno dla zwykłego obywatela jak i polityków. Natomiast ekonomiści, którzy starają się usilnie przewidywać przyszłość gospodarczą, mogą grypę hiszpankę uczynić punktem zaczepienia do oceny wpływu bieżącej epidemii. Ostatnio R. Barro et al. [1] przeprowadzili w tym celu analizę wpływu śmiertelności tego wirusa na różne zmienne ekonomiczne, jak PKB, konsumpcja, inflacja czy ceny akcji - w 43 krajach.

Po pierwsze trzeba odnotować, że średnia śmiertelność hiszpanki wyniosła 2%, czyli mniej więcej tyle co obecny wirus. Po drugie z modelu regresji wynika, że każdy dodatkowy punkt procentowy śmiertelności grypy (flu death rate) przekładał się średnio na spadek PKB o 2,98 pkty procentowe rocznie. To znaczy, że kryzys epidemiczny obniżał średniorocznie PKB na świecie o 6% (3*2%). Analogicznie dla konsumpcji parametr wyniósł -4,06, to znaczy, że konsumpcja spadała w związku z grypowym kryzysem o 8,2% (4,1*2%) rocznie.

Nie oznaczało to jeszcze, że PKB i konsumpcja w czasach zarazy rzeczywiście o tyle spadały. W regresji występują także inne zmienne, jak wpływ I Wojny Św. (jej śmiertelności), a także stała, która wynosi odpowiednio 0,02 i 0,018. Ponieważ I Wojna nas nie interesuje, to dodajemy do naszych poprzednich szacunków jedynie stałą. Czyli w naszym przypadku PKB powinno spaść o 4%, a konsumpcja o 6,4%.

Biorąc pod uwagę, że w Polsce stała będzie wynosić ok. 3%, to znaczyłoby, że nasze PKB spadłoby zaledwie o 3%. Jest to więc dwa razy lepsza prognoza niż ta, którą wykonałem ostatnim razem. Z drugiej strony współczesny świat jest zglobalizowany, a zamknięcie gospodarki jest chyba bardziej dalekosiężne i drastyczne niż 100 lat temu, więc osobiście nastawiałbym się ma większe tąpnięcie (do -5, -6%).  Chociaż trzeba też pamiętać, że dzisiejsze możliwości komunikacji są nieporównywalne.

Przyjrzymy się teraz jak hiszpanka dotknęła rynki akcji, obligacji skarbowych oraz cenobiorców. Poniższa tabela pokazuje parametry regresji dla tych zmiennych:

Każda zmienna zawiera dwie kolumny. Pierwsza odzwierciedla model typu stała + wpływ śmiertelności grypy w danym roku. Druga kolumna stanowi to samo, ale dodatkowo sprawdzono czy grypa oddziaływuje na te zmienne także w kolejnych latach, tzn. dołożono zmienną Lag of flu death rate, przy czym lag to średnia krocząca od -1 do -4 lat.

Dla akcji i obligacji drugi model jest nieistotny stat., więc tylko spojrzymy na pierwszy. Stała realna stopa zwrotu z akcji wyniosła średnio 6,3% na rok, a sama hiszpanka wywoływała średnioroczne spadki 26,2% (13,1*2%) na realnym poziomie. Czyli w czasie epidemii średnioroczna stopa zwrotu z akcji na całym świecie wyniosła ok. -20% (-26,2 +6,3) w ujęciu realnym.

Nominalnie jednak walory aż tak tragicznie nie wyglądały. Zobaczmy, że inflacja ogromnie wzrastała w roku pandemii. Parametr 10 oznacza, że 1% śmiertelności powodował wzrost inflacji o 10 pktów proc. Czyli dla 2% mamy 20 pktów proc. Dodając stałą 2,6% otrzymamy średnią inflację 23%... Czy to możliwe, żeby tyle ceny zaczęły rosnąć? Jeżeli tak, to optymistyczną informacją byłoby to, że w kolejnych latach nastąpiłby powrót do starych cen - deflacja wyniosła tyle co poprzedni wzrost spowodowany kryzysem. Żeby to zobaczyć, patrzymy na drugi model dla inflacji (kolumna 6, średnia krocząca), który tym razem jest istotny stat.

Oznacza to, że nominalnie akcje nawet mogłyby wzrosnąć w 2020, bo -0,2 + 0,23 = 3%. Mimo wszystko trzeba pamiętać, że duża inflacja jest negatywna dla akcji (zob. ten wpis).

Jeżeli już to wszystko wiemy, to jak ocenilibyśmy w tych warunkach dalsze obniżanie stóp procentowych przez NBP? Wcześniej, w art.  Trzy wskaźniki: P/BV, P/E i PLN/EUR wykazywałem czysto teoretycznie, że ta decyzja NBP jest błędna. Ale podany empiryczny argument wskazuje, że może być fatalna, nie jeśli nie katastrofalna, w skutkach. Już dziś inflacja w Polsce wynosi prawie 5% i jest najwyższa w UE.

Musimy się przygotować na trudne czasy, jeśli chodzi o naszą konsumpcję i skupić się właśnie bardziej na inwestycjach, aby zmniejszyć realne straty.
 
Literatura:
[1] Barro, R., Ursua, J. F., Weng, J., The Coronavirus and the Great Influenza Pandemic: Lessons from the "Spanish Flu" for the Coronavirus's Potential Effects on Mortality and Economic Activity, March 2020;
[2] Gaafar, A., Grypa hiszpanka – pandemia groźniejsza od wojny, 08.04.2020.

Potencjalny wpływ kryzysu wirusowego na dochody w sektorach

Dotychczas oceniłem, że bieżący kryzys spowoduje ok. 6% spadku PKB w 2020 r. To teraz ocenimy jego potencjalny wpływ na poszczególne sektory. Do poprzedniej tabeli dopisałem nowe formuły. Ogólnie wykorzystałem poprzednie dane i wzór na szereg geometryczny. W sumie zbiorcze wyniki wyglądają tak:

Pełną tabelę można pobrać stąd.

Zacznijmy od końca - PKB to suma wszystkich sektorów; mamy tutaj spadek 4,18 (w marcu i kwietniu) + 2,09 (od maja) = 6,27%. Jest to ta sama wartość co wcześniej liczyłem. Zakładam, że do końca roku PKB będzie tylko spadał, ale coraz wolniej. To znaczy w marcu i kwietniu o 25%, ale rocznie wychodzi 4,2% (25/12*2). Czyli średnio w marcu i kwietniu mamy spadek 2,1%. Zakładamy też, że od maja spada o 50% wolniej w stosunku do poprzedniego miesiąca. Wzór na szereg geometryczny można tutaj spokojnie przybliżyć szeregiem nieskończonym: a*q^0 + a*q^1 + a*q^2 +...  = a/(1-q) , czyli bardzo prosty wzór. U nas a = -2,1 / 2 , q = 1/2. Podstawiamy:
S = 2,1/2 / (1 - 1/2) = 2,1/2 / 1/2 = 2,1.

Widać, że sumaryczny spadek od maja 2020 wynosi tyle co spadek z jednego miesiąca marca lub kwietnia. Dlatego w załączonej tabeli zauważymy tę samą zależność dla wszystkich sektorów. Dochody z rolnictwa spadną w marcu i kwietniu o 8,3% i potem już tylko połowę. Sumarycznie 12,5%. Przemysł się utrzyma na tym samym poziomie (choć w rzeczywistości pewnie nieco spadnie, bo wiele firm przestaje działać, więc energia i woda także). Budownictwo - tak samo jak rolnictwo. Zyski z handlu spadną o niecałe 19% itd.

Jak "kryzys wirusowy" wpłynie na PKB w 2020?

Jeszcze do niedawna mbanki i inne instytucje prześcigały się w coraz większych prognozach wzrostu PKB. Teraz trend się odwrócił. Zaczęło się niemrawo - od spadku dynamiki do +1%, kiedy było już oczywiste, że to wizja skrajnie optymistyczna. Kiedy kolejni analitycy powtarzali negatywne prognozy, rozpoczeła się seria "kto da mniej", tak że w końcu zaczęto mówić o spadku samego PKB, a nie jego dynamiki. Odważono się wypowiedzieć to słowo: recesja. Erste niedawno podał -3,7%, teraz mbank -4,2, a PKO -4,4%.

Chociaż jest to sytuacja zupełnie nowa, której się dopiero uczymy, to możemy sami ocenić jak zmieni się PKB w 2020.

Wykorzystując dane GUS obliczyłem strukturę PKB 2019 i na jej podstawie oszacowałem możliwą strukturę na marzec i kwiecień 2020. To pozwoli ocenić skalę spadków. Dane można pobrać stąd:
Przykładowa struktura PKB

Pogrubione wartości to przykładowy szacunek struktury na marzec-kwiecień 2020. I tak np. przyjąłem, że w marcu rolnictwo skurczy się o 50%, przemysł się nie zmieni, budownictwo spadnie o połowę, a handel i transport o 75%. Być może powinno być więcej, ale nie znam się, więc tylko strzelam. Zakwaterowanie i gastronomia spadnie do 0. Itd.

Suma tych ułamków daje niecałe 75%. Oznacza to, że PKB kurczy się o 25% w marcu i kwietniu (w zasadzie wartość dodana, która teoretycznie powinna być równa PKB, ale widać, że różne metody liczenia dają trochę różne rezultaty). Jeżeli więc od maja gospodarka zostałaby w całości odmrożona, to dostajemy 2/12*25% = 4,2% spadku PKB rocznie, zakładając, że w drugiej połowie roku PKB nie będzie się zmieniać.

Jednakże po takim ciosie gospodarka nie wyzdrowieje tak po prostu, bez żadnych przeszkód. Powinniśmy uwzględnić dodatkowo "czas rekonwalescencji". Najprostszy przykład to bezrobocie. Skoro teraz firmy zwalniają pracowników, to przecież nie po to, by ich wszystkich za chwilę znowu zatrudniać. Naprawianie szkód potrwa, tak samo znalezienie pracy nie następuje z dnia na dzień. Tym bardziej, że nawet bez rządowego ataku na przedsiębiorstwa (bo przecież wirus nie jest temu winny, że plajtują), gospodarka zaczęła wchodzić w okres stagnacji. Powiedzmy więc, że czas naprawy będzie trwał w ten sposób, że z każdym kolejnym miesiącem PKB będzie spadać o 50% wolniej m/m. Skoro w kwietniu spadł średnio o 2,1% (4,2/2), to w maju spadnie o 1,05%, w czerwcu o 0,5%, w lipcu 0,25%, w sierpniu o 0,12%, wrześniu o 0,06% i w październiku 0,03%. Sumarycznie 2%. To znaczy, że dostajemy 4,2+2 = 6% spadku PKB w 2020. Ostatnie 3 miesiące to może być stabilizacja, być może z małą zmianą na plus.

Z pewnością ten kryzys zmieni świat, w tym Polskę. Nie wiemy, jaki efekt przyniesie w długim terminie. Niektóre sektory, jak sektor medyczny i tekstylny mogą zwiększyć produkcję i stworzyć nowe gałęzie. Ale jak sytuacja ukształtuje się w krótkim terminie? Wydaje mi się, że ostatni kwartał tego roku będzie najwyżej w okolicach zera, np. +0,5%, co trochę poprawi ogólny obraz recesji.
 
W sumie więc prognozuję, że w 2020 PKB spadnie o od 5,5 do 6%.

Wycena długoterminowa jest większa od krótkoterminowej

We wzorze wyceny akcji z podatkami osobistymi i kosztami transakcyjnymi oszacowana stopa zwrotu w każdym okresie zawiera prowizję kupna i sprzedaży, tak jakbyśmy chcieli trzymać akcje tylko jeden rok: na początku każdego roku dokupowali nowe akcje, a na koniec roku sprzedawali. Pokazywałem już kiedyś, że inwestor, który chce trzymać akcje tylko rok, i tak musi wyceniać je tak, jakby trzymał nieskończoność albo wiele lat, dlatego że po tym roku sprzedaje te akcje kolejnemu inwestorowi, który znów może je trzymać rok itd (dokładniej o tym tutaj). Wartość akcji zawsze będzie zawierać przyszłe oczekiwane dywidendy.

Ale powstaje teraz takie pytanie. Co jeśli inwestor chce trzymać akcje przez wiele lat, nie dokupować, a najwyżej stopniowo je sprzedawać? W tej sytuacji oczekiwana stopa zwrotu nie zawiera praktycznie w ogóle prowizji kupna (tylko na początku się kupuje, więc dla wielu lat można ją pominąć). Czyli zawiera jedynie prowizję od sprzedaży. Prowizję maklerską od sprzedaży musimy uwzględnić nawet jeśli nie sprzedajmy co roku akcji, a jedynie gdzieś na końcu. W Dodatku do art. Wycena akcji ze wszystkimi podatkami dochodowymi wykazałem, że suma podatku od zysku z sumy okresów jest równa sumie podatków od zysków poszczególnych okresów. Inaczej mówiąc sprzedaż po wielu latach prowadzi do takiego samego podatku jak sprzedaż każdego roku. Jeśli więc prowizję traktujemy jako część podatku, to ta zasada również obowiązuje w tym przypadku.

 

Ponieważ początkową prowizję od kupna pomijamy, we wzorze stopy zwrotu potrąconej o prowizje  , musimy usunąć początkowy x w wyrażeniu K1(1+x):

(1)

gdzie:
r_x - stopa zwrotu po potrąceniu prowizji ze sprzedaży
K1 - kapitał początkowy
K2 - kapitał końcowy bez potrącania prowizji
x - prowizja w %

Przekształcamy (1) i dzielimy przez K1:

Czyli dostajemy stopę zwrotu bez potrącania prowizji r:

(2)

Dostajemy:

(3)

Przekształcamy ten wzór:

(4)

Ponieważ:

(5)

Podstawiając (5) do (4):

(6)

W końcu podstawiamy (6) do (3):

i wyciągamy r_x

(7)

Przykładowo: jeśli oczekiwana stopa zwrotu z WIG = 10%, to stopa zwrotu po odjęciu samej prowizji sprzedaży wyniesie 0,1*(1-0,0039)-0,0039 = 9,6%.

Teraz wrócimy do artykułu z wyceną ze wszystkimi podatkami osobistymi i prowizją maklerską> Wzór był następujący:

Jednak tutaj g(1 - t_x) = r_x. Aby nie mylić nazewnictwa, nazwiemy g_x = r_x i wtedy oznaczymy:

 (8)

Wartość wewnętrzna akcji przyjmie postać:
 (9)

Podstawiamy (8) do (9):

(10)

Przykład
Porównamy wycenę AMC poprzednią metodą z obecną. Oczywiście sytuacja się znacznie zmieniła, co należy jednak uznać za wypadek losowy. Chociaż sytuacja się znacznie pogorszyła, to przypomnę, że koszt kapitału mógł nawet spaść, o czym pisałem tutaj . Wprawdzie chodziło tam o małe spółki, ale AMC obecnie należy do średnich, więc też jej dotyczy. Dane jak poprzednio

Dla g = 7,5%:

Poprzednio było to 108.
Dla g = 8,5%:

Wcześniej było 144.

"Kryzys wirusowy" jest na tyle losowy, że można go uznać za zjawisko krótkoterminowe i przez to nie da się go uwzględnić w tak prostej wycenie.

Wniosek intuicyjny: dla inwestora krótkoterminowego wartość akcji jest mniejsza niż dla inwestora długoterminowego. To powoduje racjonalną wymianę walorów. Długoterminowi będą uznawać akcje za niedowartościowane, które krótkoterminowi uznają za prawidłowo szacowane lub nawet zbyt drogie. Krótkoterminowi będą mieć więc większy problem z kupieniem akcji tanich, ale za to będą w korzystniejszej sytuacji, jeśli chodzi o możliwość sprzedaży, ponieważ będą skłonni sprzedawać po niższej cenie.

Trzy wskaźniki: P/BV, P/E i PLN/EUR

Chociaż to wróżenie z fusów, to poniższe wykresy dają pogląd na dalszy możliwy rozwój wydarzeń:

Warto dodać, że dla miesięcznych danych od 10.2007 r. P/BV i PLN/EUR są silnie skorelowane - wsp. Pearsona wynosi 0,66. Między P/E a złotym korelacja jest słabsza, bo 0,39. Skoro współczynnik determinacji to kwadrat wsp. Pearsona, to możemy powiedzieć, że za 66%^2 = 44% ruchu WIG odpowiada kurs złotego. (Prognozowanie miesięczne jest trudniejsze, bo już korelacja między stopami zmian obydwu wskaźników równa się 0,5, czyli R^2 0,25).

Kurs walutowy wskazuje ile pieniędzy napływa do gospodarki. Gdy jest wysoki, to znaczy, że zagranica chce inwestować w naszym kraju, czyli popyt na złotówki rośnie. Gdy jest niski, na odwrót.

Obecnie niski kurs walutowy wynika nie tylko z "kryzysu wirusowego", ale także ostatniego obniżenia stóp procentowych przez NBP do najniższych historycznie poziomów. Gdy jest niska stopa procentowa, to zagranica niechętnie kupuje polskie obligacje, tzn. że popyt na złotówkę spada. Z drugiej strony chętniej zaciąga kredyt w PLN, który musi zamienić na swoją walutę, co jest tożsame ze sprzedażą PLN. Tak więc podaż PLN rośnie, a jeśli podaż rośnie, to cena spada - czyli kurs walutowy.

Co to oznacza? Że na spadek kursu walutowego nałożyły się powyższe dwa efekty. Teraz skutek będzie taki, że złoty jeszcze spadnie. Czy przełoży się to na dalsze spadki indeksów? Niekoniecznie. Pamiętając, że spadek złotego wynika także (albo głównie, bo pamiętajmy, że z naszej strony popyt na euro także stanął) z obniżenia stopy procentowej, która z kolei powinna działać pozytywnie na inwestycje, a więc i PKB. Oczywiście ta redukcja stóp ma sens tylko wtedy, gdy inflacja nie szaleje, a przecież obecnie już jest wysoka.

Ten ruch NBP ze stopami to błąd, bo przecież to załamanie nie ma nic wspólnego z gospodarką, ale sztucznie zostało wywołane przez władze. Pomyślmy: po co obniżać stopy, by przywrócić inwestycje, skoro samemu się te inwestycje zatrzymało? Nie może to wywołać żadnej pozytywnej reakcji, a jedynie sprowokuje wzrost inflacji, giełda z kolei nie lubi inflacji (Czy inflacja jest dobra dla akcji?). Czyli paradoksalnie niższe stopy pogorszą sytuację. Tym samym rząd "zagwarantował" nam dalsze osuwanie się indeksów.

Mały plus z tego krachu

Panika z jaką obecnie mamy do czynienia oczywiście przejdzie do historii, ale na przekór moglibyśmy wyciągnąć z niej coś pozytywnego dla drobnych inwestorów. W normalnej bessie wielcy gracze są zawsze lepiej poinformowani i wiedzą wcześniej, kiedy należy się wycofać albo wejść do gry. Tutaj jednak sytuacja jest dla nich tak samo nieprzewidywalna i zaskakująca jak dla każdego. "Grubasy" dowiadują się o skutkach koronawirusa mniej więcej w tym samym czasie co wszyscy inni. Jest to wyjątkowy czas, gdy drobny inwestor ma taką samą szansę jak duży, jeśli chodzi o przewidywania gospodarcze. To znaczy, że zmniejsza się asymetria informacji, a przez to spada koszt kapitału własnego.

Największa asymetria informacji występuje rzecz jasna na małych spółkach. Jeśli więc teraz się ona zmniejsza, to dostajemy sygnał, że powinniśmy się baczniej przyjrzeć sWIG80. Gdy porównamy ten indeks z dużymi spółkami, to okaże się, że obecny krach - przynajmniej na razie - różni się nieco od typowej bessy. Małe spółki były bardziej wrażliwe na dane makro, siła spadków była większa. Tym razem jest inaczej. Spójrzmy z perspektywy:

I jeszcze w porównaniu z WIG30 w krótkiej perspektywie, od 20 lutego 2020, czyli od dnia, gdy zaczęły pojawiać niepokojące sygnały, że wirus może dostać się do Polski:

Obecnie różnica w spadkach wynosi ponad 10 pkt proc na niekorzyść WIG30. Chociaż regulacje rządów poprzez wprowadzanie kolejnych zakazów w handlu, transporcie itp. mogą mieć gorsze reperkusje dla small-capów niż blue-chipów, to paradoksalnie te pierwsze zachowują się lepiej. Wytłumaczyć to można na dwa sposoby. Po pierwsze duzi traderzy grają głównie na płynnych walorach, a teraz ze względu na równy dostęp do informacji, muszą pozbywać się papierów od razu, a nie małymi pakietami, przez co zwiększają podaż. Po drugie, jak wcześniej napisałem, nagle asymetria informacji przestała jakby istnieć, tak że koszt kapitału małych spółek zmniejszył się. Dodam tu, że wpływ asymetrii informacji na koszt kapitału własnego został udowodniony w różnych opracowaniach. Np. C. Botosan ("Disclosure level and the cost of equity capital", Jul 1997) oszacowała, że dla spółek o małym zainteresowaniu analityków każda dodatkowa różnica w jawności informacji wiąże się z różnicą ok. 28 pktów bazowych  w koszcie kapitału. Dla spółek o dużym zainteresowaniu nie znaleziono takiego związku.

Strategia spółki wobec rynku akcji

Krótko na temat tego jak spółka może albo powinna podejmować działania w kontakcie z rynkiem. Temat jest wielopłaszczyznowy, ale w uproszczeniu moglibyśmy powiedzieć, że są dwie przeciwstawne perspektywy spółki. Z jednej strony powinna ona maksymalizować swoją wartość, czyli zarabiać jak najwięcej i płacić jak największe dywidendy. Oznacza to, że jeżeli spółka widzi swoje niedowartościowanie na rynku, to powinna przestać wypłacać bieżące dywidendy, a zacząć wykupywać swoje akcje w celu umorzenia, doprowadzając do zrównania ceny z wartością wewnętrzną. Uzyskane oszczędności będą zasilać kasę spółki i zwiększać wartość księgową, z czasem uwalniać się w postaci nadwyżek dywidendy. Jeżeli z kolei widzi przewartościowanie, należy zwiększać wypłatę bieżących dywidend, a potrzebny do tego kapitał uzyskiwać poprzez emisję nowych akcji. Dalej, moglibyśmy się nawet spodziewać, że spółka będzie emitować akcje nie tyle na teraźniejsze dywidendy, co na przyszłe inwestycje, na wszelki wypadek, aby mieć nadwyżkę pieniężną. Jeżeli zaś akcje byłyby prawidłowo wycenione, spółka płaciłaby optymalnie dywidendy do takiego poziomu, aby nie ograniczały inwestycji oraz nie redukowały rentowności.

Z drugiej strony, spółka, szczególnie o małej kapitalizacji, może swoimi działaniami sygnalizować rynkowi swoje niedowartościowanie lub przewartościowanie. W tej sytuacji zachowuje się tak samo jak wyżej opisałem, ale tym razem nie gra z rynkiem, a jedynie się z nim komunikuje.

W pierwszej perspektywie firma chce kupić swoje akcje jak najtaniej i emitować akcje jak najdrożej. Inwestorzy są więc jej rywalami. W drugiej firma z nikim nie rywalizuje, a jedynie koryguje stosunek inwestorów do niej samej.

Te dwie różne perspektywy prowadzą do odmiennych zachowań. W pierwszym przypadku spółka ogłasza wykup akcji własnych po kursie zbliżonym do bieżącego (w granicach na minus i plus obecny kurs). W drugim przypadku spółka podaje cenę nabycia równą wartości wewnętrznej czyli dużo wyższą niż bieżąca. Łatwo się domyślić, że po tej informacji kurs wzrośnie.

Wniosek jest więc taki, że jeżeli spółka ogłasza nabycie akcji po cenie zbliżonej do obecnej, to nie znaczy wcale, że taka jest faktyczna wartość wewnętrzna, przynajmniej wg spółki. Będzie to po prostu strategia na grę z rynkiem. I podobnie w przypadku emisji akcji - cena zbliżona do rynkowej będzie prawdopodobnie oznaczać, że jest ona zawyżona.

Kolejny wniosek z tej analizy płynie taki, że każde ogłoszenie nabycia akcji własnych jest pozytywną informacją dla akcjonariuszy, a każda emisja - choć nie jest to zawsze pewne - może być uznane za negatywną. Stąd ceny akcji często zachowują się właśnie tak, że ta pierwsza prowadzi do wzrostów, a druga do spadków.

Ostatni wniosek: spółka nie powinna płacić dywidendy, jeżeli akcje są niedowartościowane. Ta konkluzja pozornie przeciwstawia się tezie zawartej w artykule Inwestując w akcje oczekujmy dużych dywidend . Tam stwierdziłem, że nabycie akcji własnych to jedna wielka strata dla akcjonariusza, jeżeli spółka zamiast dywidendy, kupuje swoje akcje. Różnica polega na tym, że w tamtym artykule od początku zakładałem, że akcje są prawidłowo wycenione. Może to założenie powinno być tam dopisane, żeby nie było wątpliwości. Gdy cena jest równa wartości wewnętrznej, to spółka powinna płacić tylko dywidendy i nie nabywać już akcji własnych. A co z emisją akcji? W tym przypadku także powinniśmy mieć podejście krytyczne, bo jeśli spółka chce korzystać z zewnętrznego finansowania, to powinna wybrać obligacje albo kredyt, co wyjaśniłem w art. Inwestor czy frajer?

Wycena akcji z podatkami osobistymi i kosztami transakcyjnymi

Obecnie wiadomo już, że wycena akcji Gordona ze wszystkimi podatkami osobistymi jest następująca (zobacz Dodatek lub ostatni wpis):

(1)

gdzie:
P - wartość wewnętrzna akcji
D - oczekiwana dywidenda brutto w kolejnym okresie
t_d - stopa podatku od dywidendy brutto
t_s - stopa podatku od zysku ze sprzedaży akcji
r - koszt kapitału własnego po odjęciu wszystkich podatków osobistych
g - oczekiwana stopa wzrostu dywidendy brutto (jednocześnie równa oczekiwanej stopie wzrostu wartości wewnętrznej)

Normalnie powiedzielibyśmy, że t_d = t_s = 19% w Polsce. Jednak do t_s możemy od razu dorzucić koszt transakcyjny. Napisalibyśmy więc tak:

(2)

gdzie t_x to "podatek od transakcji".

Wartość akcji (1) możemy przekształcić:

(3)

Stopa t_x nie jest kosztem transakcyjnym od aktywów, ale od stopy zwrotu. Żeby sprowadzić go do tej formy, posłużymy się wzorem (który wyprowadziłem tutaj) na stopę zwrotu po potrąceniu prowizji:

(4)

gdzie x - koszt transakcji od wartości akcji, a N to liczba transakcji.

Dlaczego używam tutaj zapisu g_p zamiast r_p? Dlatego że jak wiadomo g to nie tylko stopa wzrostu dywidendy, ale także ceny akcji. Zakładamy, że na początku każdego okresu płacimy prowizję od kupna, a na końcu okresu prowizję od sprzedaży. Ponieważ wzrost ceny, g_p, dotyczy pojedynczego okresu, np. roku, to znaczy, że N = 1. W każdym roku będzie więc jedna sprzedaż. Napiszemy więc:

(5)

Następnie, ponieważ g odpowiada wzrostowi ceny:

(6)

A g_p to wzrost ceny, ale po odjęciu prowizji:

(7)

to znaczy, że:

(8)

Czyli (5) = (8):

I stąd wyznaczamy t_x:

(9)

Dodatkowo przekształćmy (9):

(10)

Możemy w końcu wrócić do wyceny akcji. Czyli (3) możemy zapisać tak:

(11)

Ponieważ jednak w g_p siedzi tylko jedna transakcja sprzedaży na okres, to znaczy, że:

(12)

są tożsame, co widać, gdy spojrzymy na (9). Prawa strona (12) to stopa zwrotu z jednej transakcji sprzedaży (przy uwzględnieniu prowizji za kupno i sprzedaż), którą wyprowadziłem tutaj. W sumie ostatnie wyrażenie (11) na cenę możemy przedstawić także w następującej formie:

(13)

Przykład.
Zrobię prostą wycenę AMC.
1) Oczekiwany zysk: w 3 kwartały 2019 narastająco spółka zarobiła na czysto 70,57 mln zl. Średnia z tych 3 kwartałów to 23,523 mln zł. W sumie prognoza na 2019 będzie to 70,57+23,52 = 94,1 mln zł.

2) Oczekiwana dywidenda i wzrost dywidendy: wg komunikatów spółki dywidenda ma wynosić 35% zysku netto. Czyli w 2020 byłoby to ok. 4,2 zł na akcję. Te 4,2 będzie punktem wyjścia. Nie jest to jeszcze D, ponieważ to bardziej teraźniejsza dywidenda, a chcemy mieć na rok następny. Spółka sugeruje wzrost przychodów w kilku kolejnych latach o 5%, a potem nieco wyższy. Historycznie spółka rośnie szybciej niż 5%. Prognoza ARMA(0, 2) warunkową metodą największej wiarygodności (CMNW, dla bardzo długich terminów wydaje się lepsza - zob. ten wpis) wskazuje, że prognozowana średnia stopa wzrostu przychodów = 6,4%:

Dane historyczne - od 2004 do 2018.

Z kolei EBIT prognozowany za pomocą ARMA(3,1) , też CMNW, w długim terminie - na poziomie 15,9%:

Wzrost przychodów nie odpowiada zmianom dywidend, skoro EBIT historycznie rośnie średnio 2,5 razy szybciej. Zysk netto rośnie jeszcze więcej. Gdyby przyjąć, że spółka miałaby rozwijać sprzedaż w tempie 5% w kolejnych latach, to przyjmując proporcjonalność, zysk operacyjny będzie rósł ok. 2,5 razy szybciej, tj. 12,5%. Taki poziom jest raczej nie do utrzymania, choćby z tego powodu, że już historyczne ROE (też od 2004) wynosi niecałe 11%, jak się za chwilę okaże tyle co koszt kapitału własnego. Skoro wskaźnik wypłaty dywidendy = 35%, to znaczy, że oczekiwany wzrost powinien wynieść 11*(1-35%) = 7,15%. Ponad dwukrotna różnica między historycznym 16% a 7% wynika z dużej zmienności ROE. Trzeba pamiętać, że oczekiwany wzrost zysku to część zatrzymanego zysku razy średnie ROE plus zmiana ROE w czasie. Średnia zmiana ROE wyniesie zero, ale większe odchylenie standardowe ROE będzie podnosić średnie g (szczegółowe wyjaśnienie tutaj).

Aby delikatnie uwzględnić tę zmienność ROE, która może w dalszych latach też mieć znaczenie, zwiększę g z teoretycznego 7,15% do min. 7,5%, a max do 8,5%. Będzie to bardziej prawidłowe z punktu widzenia historii i klasycznej ekonometrii. W sumie dla naszych potrzeb założymy w uproszczeniu, że g = 7,5-8,5%, a także D = 4,2*1,075 = 4,52 i 4,2*1,085 = 4,6.

3) Koszt kapitału własnego: wg rocznych stóp zwrotu w latach 1999-2019 współczynnik korelacji z WIG wyniósł 0,43. Odchylenie standardowe stopy zwrotu AMC wyniosło 60,8%, a WIG 25,3%. Średnia stopa zwrotu (zmiana ceny + stopa dywidendy) wyniosła dla AMC 25,5%, a dla WIG 10,65%. Stopa wolna od ryzyka powinna w kolejnych latach rosnąć, ponieważ stopa % jest od długiego czasu bardzo niska, najniższa w historii, inflacja rośnie, a więc Bank Centralny powinien w końcu podnieść stopy, a nie ciągle zaklinać rzeczywistość, że to tylko przejściowy wzrost cen. Wolną stopę, r_f, ustawimy w zakresie 2,5-3,5%. Niech będzie 3%, bo różnice w wycenie będą niewielkie. Stosujemy wzór na CAPM:

(14)

Podstawiając dane otrzymałem k = 10,86%.

Uwaga techniczna: jeśli stosujemy wzór z kowariancją, to musi to być kowariancja z próby. Ta standardowa z Excela to kowariancja z populacji i musi być wtedy przemnożona przez n/(n-1), gdzie n to liczba okresów. Dopiero taki wzór stanie się równoważny z (14).

Wzór (14) to nie jest pełny koszt kapitału. Żeby go uzyskać, należy odjąć podatki osobiste i koszty transakcyjne (zob. ten art.). Nie byłoby żadnego problemu, gdyby x = 0, bo wtedy t_d = t_s i wówczas wystarczyłoby odjąć 19% od k. Gdy x > 0, t_s > t_d, więc sytuacja się komplikuje. Jednakże w ostatnim artykule dowodziłem, że dla płynnych walorów wzrost t_s (oznaczana tam PIT_k) nie spowoduje spadku oczekiwanej stopy zwrotu, ponieważ wzrost t_s automatycznie powoduje spadek popytu na te akcje (czyli spadku bieżącego kursu), a więc oczekiwana stopa r pozostaje stabilna.

Patrząc powierzchownie myślelibyśmy, że dodatkowa opłata zmniejszy nasz przyszły zysk. Jednak trzeba spojrzeć na sprawę ekonomicznie, szerzej. Jeśli inwestorzy są racjonalni, to obniżą wartość tych aktywów, które obarczone są większym kosztem. Ponieważ wartość księgowa tych aktywów się nie zmieniła, a przecież jest ona silnie skorelowana z oczekiwanym cash flow, to znaczy, że w przyszłości, gdy będzie likwidacja spółki i wypłacana ostatnia dywidenda, inwestor nie będzie już płacił kosztów transakcyjnych, a to oznacza, że im bliżej likwidacji, tym wartość rynkowa musi zbliżyć się do księgowej.

Na sprawę można też spojrzeć w ten sposób, że cena została pomniejszona już o koszty transakcyjne, a wobec tego stopa dyskontowa jest powiększona o nie. Generalnie nie jest jasne czy cena waloru powinna być pomniejszona o koszt transakcyjny (a stopa dyskontowa powiększona o nie) czy powiększona (stopa pomniejszona). Patrząc jednak szerzej, lepszym ujęciem wydaje się to pierwsze, ponieważ koszt transakcyjny można potraktować jak złą wiadomość gospodarczą. 

Czy z podatkiem od dywidendy i od sprzedaży akcji będzie tak samo jak prowizją maklerską? W praktyce w krótkim okresie tak, jednakże teoretycznie już nie do końca. Od kosztów transakcyjnych raczej nie można uciec, natomiast z podatkami jest inaczej. Podatki wymuszą racjonalną zmianę struktury kapitałowej - bardziej opłaca się zadłużenie niż kapitał własny (inwestor nie płaci wówczas podwójnego podatku od dochodu). Firma zacznie więc wykupywać akcje własne i zamieniać na obligacje, ewentualnie kredyty. Wtedy obniżka ceny spowodowana podatkiem od dywidend czy dochodów kapitałowych będzie skompensowana większym zyskiem na akcje. W długim okresie cena się wyrówna (pisałem o tym tutaj): dywidenda spadnie (przez podatek), ale stopa dyskontowa też spadnie. Licznik i mianownik zmniejszą się o tyle samo, co wyrówna cenę.

W sumie, aby uzyskać r z (13) powinniśmy odjąć t_d, dokładniej r = k*(1 - t_d) , co jest jednoznaczne z sytuacją, gdy koszty transakcyjne nie występują (porównaj pierwszy wzór  w Dodatku). Ale przecież gdy tak podstawimy do (13), to (1-t_d) się skróci i zostanie znów samo k. Czyli do (13) zwyczajnie podstawimy tylko k i podatek od dywidendy znika:

(15)

Dostaliśmy więc wycenę, gdzie jedynym dodatkowym kosztem będzie koszt transakcyjny, natomiast podatki od dywidend i dochodów kapitałowych nie mają wpływu.

5) Podstawianie

W końcu możemy podstawić wszystkie dane do (15). Dla g = 7,5%:

Dla g = 8,5%:

W ostatnim roku kurs porusza się w tym marginesie:

Zauważmy, że gdyby zastosować tradycyjną wycenę Gordona, tj. dla x = 0, to dostalibyśmy dla pierwszej wersji g  134 zł, a dla drugiej 195, czyli zbyt wysokie granice dla obecnego kursu.


Dodatek:

Oczekiwana stopa zwrotu = zwrot z dywidendy netto + zwrot ze sprzedaży akcji po aprecjacji jej ceny i odjęciu prowizji:

Wyznaczamy stąd cenę akcji:

W kolejnym okresie analogicznie:

Czyli P0 można zapisać jako:

Dla okresu P(2):

 

 Znów podstawiamy do P(0):

Powtarzając ten schemat w nieskończoność dostaniemy sumę zdyskontowanych dywidend:

  Zakładając, że dywidenda brutto rośnie w przeciętnym tempie g, podstawimy za D2 = D1*(1+g) itd.:

Teraz spójrzmy, że cenę P(1) możemy zapisać analogicznie:

Ale ponieważ D(2) = D(1)*(1+g), to otrzymamy:

Wtedy cena akcji będzie też rosnąć średnio w tempie g:

Wzrost ceny o g nie jest równoznaczny ze wzrostem zysku o tyle. Rzeczywista stopa wyniesie:

Stopę g' można interpretować jako stopę netto z aprecjacji ceny. Dostajemy uproszczony zapis P(0):

Jeżeli będzie spełniony warunek:

czyli inaczej 

(tj. koszt kapitału własnego netto musi być wyższy od stopy wzrostu netto),

to nieskończony szereg geometryczny P(0) sprowadzi się do postaci:

 

Wiedząc, że g' = (1 + g)(1 - t_s) - 1, przekształcamy:

Tym samym otrzymaliśmy wzór (1).