Współczynnik Kaitza jako predyktor giełdy?

Zgodnie z hipotezą efektywnego rynku wszelkie informacje mające wpływ na wartość aktywa są uwzględnione przez cenę rynkową tego aktywa natychmiast po ich ujawnieniu się. Oznacza to, że jeśli np. teraz pojawia się informacja o stanie gospodarki, to za moment zostanie ona zdyskontowana przez giełdę. W ostatnich 3 artykułach wskazywałem na prace sugerujące negatywny wpływ płacy minimalnej (PM) na gospodarkę poprzez wzrost bezrobocia albo inflacji. Np. Dańska-Borsiak [1] doszła do wniosku, że wzrost współczynnika Kaitza (WK), czyli stosunku płacy minimalnej do przeciętnej, zwiększa stopę młodych bezrobotnych z rocznym opóźnieniem. Jeżeli rynek jest efektywny, to ceny akcji powinny spaść natychmiast po informacji, że nastąpi wzrost WK. Nie ma więc znaczenia data wprowadzenia nowej PM, a tym bardziej nie powinno być żadnego wpływu po roku, gdy wystąpią już spadki inwestycji czy PKB.

Przetestowałem więc tę hipotezę, porównując zmiany logarytmicznego WIG ze zmianami logarytmicznego WK z opóźnieniem 1 roku dla Polski w latach 1995-2015 (20 obserwacji minus 1 z powodu opóźnienia). Dane roczne WIG wzięte ze stooq.pl, natomiast zmiany WK obliczyłem, wykorzystując strony Mpips , GUS. Okazuje się, że autokorelacja Pearsona między log-stopami WIG oraz log-stopami WK (ale tylko opóźnionego o 1 rok) jest ujemna i wynosi -0,375 przy p value  = 0,1132. Trzeba tu jednak zwrócić uwagę, że korelacja rang Spearmana wynosi 0, co sugeruje, że może nie chodzić tu o sam znak (kierunek) skorelowania skorelowania, ale o siłę. Następnie w Excelu zrobiłem klasyczną regresję liniową:

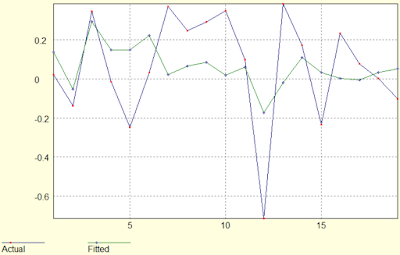
Jak widać p-value identycznie na poziomie 0,1132 wskazuje na bliską istotność na poziomie 10%. Średnia elastyczność wychodzi na poziomie -2,31, co oznacza w tym przypadku, że wzrost WK o 1 pkt proc. wywoduje średnią log-stopę WIG na poziomie -2,31% w następnym roku. Trzeba dodać jednak, że dopasowany R^2 jest poniżej 10%, co wskazuje, że model nie posiada mocy predykcyjnej. Porównać można to z wykresem, na którym zmienna opóźniona log-stopa WK(-1) stanowi wartość aktualną (actual), a log-stopa WIG wartość dopasowaną (fitted):

Wykres actual nie uwzględnia roku 2015, bo prognozowany kolejny rok 2016 jeszcze się nie skończył. Stąd dziś możemy prognozować stopę na 2016 i 2017. Na końcu roku 2015 log-stopa WK wyniosła ok. +2,5% (ln[WK(2015)/WK(2014)] = 2,5%; WK(2015) = 1850/3899,78 = 0,474; WK(2014) = 1750/3783,46 = 0,4625) lub inaczej log-WK wzrósł o 2,5%. Możemy prognozować, że pod koniec 2016 r. log-WIG spadnie o 2,5%*2,31 = 5,78%. Gdyby przekształcić to do zwykłej stopy, dostalibyśmy exp(-0,0578)-1 = -5,61%. Przypomnę jednak, że takie przekształcenie dostarcza tylko informacji o medianie (zob. Czy mediana jest lepsza od średniej?), a nie wartości oczekiwanej. Aby uzyskać wartość oczekiwaną stopy możemy posłużyć się estymatorem Duana dla dowolnego rozkładu, ale najlepiej by nie był lognormalny (zob. Smarujący estymator). "Smarujący estymator" Duana ma następującą postać:

(1)

 

Jest to minimalnie bardziej ogólna postać niż ta, którą podałem w artykule Smarujący estymator , bo tam czas był zmienną objaśniającą, która się redukowała po zamianie na stopę; smarujący estymator jest szczegółowo opisany w [2]. Sumę exp(składnik losowy(t)) uzyskałem w Gretlu. Podstawiam dane do (1):

Zatem powinniśmy oczekiwać, że WIG z końca 2015 spadnie o niecałe 3% na koniec 2016. Z dzisiejszego punktu widzenia oznacza to poziom ok. 45070 i od obecnego punktu (18.11.2016) prognozuje to ok. 4% spadku:

Dodatkowo policzmy jeszcze potencjalną zmianę w 2017. Ostatni komunikat GUS głosi, że płaca przeciętna wyniosła w 3 kw. 4055 zł. Zakładając, że na koniec 2016 r. będzie to 4060 oraz wiedząc, że od początku 2017 r. PM = 2000 zł, możemy obliczyć WK(2016) = 2000/4060 = 0,49. WK(2015) = 0,474, stąd ln(0,49/0,474) = 0,0332. Mediana zwykłej stopy będzie w takim razie wynosiła ok. exp(-0,0332*2,31)-1 = -7,38%. Gdyby założyć, że suma składników losowych jest taka sama jak w 2015, to podstawiając do (1) prognozowalibyśmy następującą oczekiwaną stopę zwrotu WIG w 2017:

Czyli przy takich założeniach WIG spadłby o kolejne 4,6%. Jednak tak jak wspomniałem, moc predykcyjna jest zbyt słaba by traktować poważnie taki model. Może jednak wskazywać siłę kierunku zmian cen: jeśli w jednym okresie WK rośnie, to w następnym WIG może wolniej wzrosnąć (czy po prostu spaść).


Warto jeszcze spojrzeć na profesjonalne prace, np. Bella i Machina, którzy wykorzystują tzw. analizę zdarzeń do oszacowania efektywności brytyjskiego rynku na wiadomość o podniesieniu PM [3]. Anomalną (abnormal) skumulowaną stopę zwrotu z akcji spółek, które zatrudniają pracowników na PM, autorzy porównali z teoretyczną stopą CAPM przed i po komunikacie. Wyniki pokazują, że w obydwu przypadkach wartości rynkowe istotnie spadały. W ciągu 10 dni od ogłoszenia ceny tych firm były niższe o ok. 3%. Zbiorowe wyniki przedstawia poniższa tabela:

 NMW - National Minimum Wage jest to zmienna sztuczna (dummy), która przyjmuje wartości 1 (firma zatrudnia wielu za PM) lub 0 (firma nie zatrudnia wielu za PM).
 Najważniejsza wydaje się tu kolumna (1) i (2). Wiersz NMW - Kolumna (1) wskazuje, że anomalna 15-dniowa stopa zwrotu wyniosła -2,6% i jest istotna na poziomie 1% istotności. Kolumna (2) uwzględnia dodatkowe czynniki (literka Y), jak np. wielkość spółki lub to czy przed ogłoszeniem nowej PM stopy spadały. Wtedy efekt nawet rośnie: firmy, które zatrudniają za PM, o prawie 4% tracą nadmiernie na wartości. Sytuację ilustruje poniższy wykres:

 
Podsumowując, można powiedzieć, że wpływ zmiany płacy minimalnej na rynek akcji jest istotnie negatywny, co więcej można przypuszczać, że stanowi jedną z anomalii rynku akcji, pozwalając prognozować spadek stóp zwrotu.


Literatura:

[1] B. Dańska-Borsiak, Płaca Minimalna A Liczba Młodych Pracujących. Związki Przyczynowe I Prognozy Wariantowe, Uniwersytet Łódzki, 2014,
[2] N. Duan, Smearing Estimate: A Nonparametric Retransformation Method, Sep. 1983,
[3] B. Bell, S. Machin, Minimum Wages and Firm Value, Nov. 2015.

Źródło danych:
http://stooq.pl/
http://stat.gov.pl/
http://www.mpips.gov.pl/