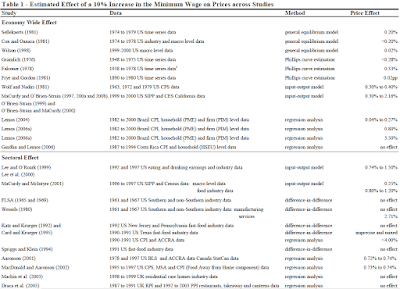
Źródło: Lemos, S. [4]
Co do drugiej części, czyli efektu sektorowego, to nie trudno się było domyślić, że największy efekt wypadnie w sektorze żywności (ale nie sieci fast-foodowych), bo ok. 1% - przynajmniej w USA.
Sceptycy zwróciliby uwagę na miejsca, gdzie nie wykazano żadnego efektu, jak w Wielkiej Brytanii. Nie oznacza to jednak, że efektu nie było w ogóle. Przede wszystkim Lemos uwzględniła istotność statystyczną tych artykułów. Tam gdzie zabrakło tej istotności, wpisała "no effect". Wziąłem pod lupę ostatnią pracę na liście, Draca et. al [1] i muszę stwierdzić, że mam co do niej spore uwagi. Wg artykułu w Wielkiej Brytanii wprowadzono PM w kwietniu 1999 r., tak że średni przyrost płac wyniósł ok. 10%. Badano kantyny, restauracje i posiłki na wynos. Autorzy konkludują, że nie znaleźli znaczącego wpływu wzrostu PM na ceny. Jednak wcześniej możemy przeczytać, że jedyny istotny statystycznie efekt wystąpił w sektorze kantyn (stołówek) w kwietniu 1999 r., bo 1 pkt proc. To znaczy, wzrost PM o 10%, wywołał realnie wzrost cen posiłków w kantynach o 1%. A przecież jest to zgodne z wynikami, jakie znalazła Lemos w innych pracach w sektorze żywności. Tak więc efekt nie jest zerowy. Żeby to uwiarygodnić poniżej wklejam rysunek z tej pracy, na którym możemy porównać zmiany cen dla każdego z 3 sektorów.
Źródło: Draca, M. et al. [1]. NMW - national minimum wage (krajowa płaca minimalna).
Widzimy, że w kantynach ceny przyspieszyły z rocznym opóźnieniem, natomiast dla restauracji i jedzenia na wynos rzeczywiście nie dostrzegamy różnicy przed i po wprowadzeniu PM.
W tym miejscu chciałbym też zwrócić uwagę, że inflacja żywności może posłużyć do oszacowania całkowitej inflacji. Załóżmy, że ceny żywności rosną o 1%, ale pozostałe produkty i usługi pozostają stałe. Mamy równanie:
Inflacja = W1*(inflacja żywności) + (1 - W1)*(inflacja pozostałych elementów koszyka),
Inflacja = W1*0,01 + (1 - W1)*0 = W1*0,01,
gdzie:
W1 - waga żywności w koszyku inflacji
W2 - waga pozostałych produktów i usług.
Na portalu money.pl (tutaj ) znalazłem taką grafikę:
Źródło: money.pl
Widzimy, że W1 = 25%. Podstawmy:
Inflacja = 25%*0,01 = 0,25%.
Czyli otrzymaliśmy potwierdzenie pierwotnej tezy, że 10% wzrostu PM wywołuje średnio 0,25%-0,3% wzrostu cen.
Sceptycy po pierwsze zwróciliby uwagę, że 0,3% w stosunku do 10% to kropla w morzu, stąd efekt jest praktycznie zerowy. Po drugie wyniki zachodnich krajów nie muszą przekładać się na Europę Środkowo-Wschodnią. Zacznijmy od drugiego kontrargumentu. Obala go praca Harasztosiego i Lindnera [2]. Od 2000 do 2001 r. prawicowy rząd węgierski podniósł PM realnie o 60%, a w kolejnym roku o 25%. W sumie w ciągu 2 lat PM poszła w górę o 100%. Nie miało to dramatycznego wpływu na gospodarkę, tempo PKB przed i po zmianach oscylowało w okolicy 4%. Jednak wpływ na inflację był duży. Spójrzmy na poniższą tabelę:
Źródło: Harasztosi, P., Lindner, A. [2]
W panelu A obserwujemy krótkoterminowy wpływ zmiany PM na ceny przemysłu. W kolumnie (1) znajduje się model typu jedna zmienna (zmiana PM) plus stała. Dwuletni efekt podniesienia PM o 100% wyniósł 7,6% wzrostu cen w przemyśle. Stała, która wynosi 16% może być interpretowana jako inflacja spowodowana innymi czynnikami. Te inne czynniki zostały rozbite w kolumnie nr (2) i (3). Nie zaznaczałem kolumny (2), bo pełne ujęcie dodatkowych zmiennych kontrolnych zostało zawarte właśnie w (3). Po odjęciu tych innych czynników, wpływ wzrostu PM stał się mniejszy i wyniósł ok. 5%.
W panelu B znajdziemy to samo, ale dla długiego okresu, od 2000 do 2004. W długim okresie efekt sumarycznie się znacznie zwiększył. Bez zmiennych kontrolnych ceny średnio urosły o 13,7%, natomiast z tymi zmiennymi efekt nawet się sporo zwiększył - do 14,6%. Warto też zwrócić uwagę na sumaryczną inflację w ciągu tych 5 lat, nie wynikającą ze wzrostu PM. Chodzi tu o stałą, 27%.
W panelu C znajdziemy test "placebo", tj. to samo dla lat poprzedzających, 1998-2000. W tym okresie PM także rosła, ale wolniej i nie znaleziono żadnego efektu.
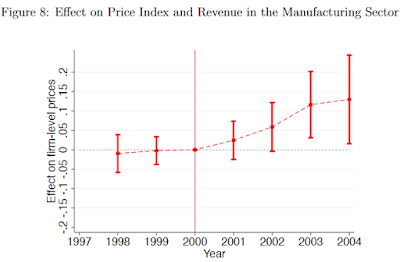
Poniższy rysunek podsumowuje wyniki tej tabeli:
Źródło: Harasztosi, P., Lindner, A. [2]
Przekształćmy teraz te dane, tak aby oszacować wpływ wzrostu PM o 10% na ceny. 100% wzrostu PM przekłada się na wzrost cen o 14,6% w ciągu 5 lat. Ponieważ model jest liniowy, możemy podzielić to na 10. 10% wzrostu PM daje 1,46% inflacji. Rocznie jest to 0,29% (1,0029^5).
Faktem jest, że inflacja 0,3% jest tak niska, że niemal zaniedbywalna. Ale jest to tylko efekt występujący bezpośrednio po wprowadzeniu zmian w ciągu roku, natomiast skumulowany efekt w kolejnych latach rośnie kilkukrotnie, tak że 10% wzrostu PM przekłada się w całości na wzrost cen o ok. 1,5%.
Podsumowanie:
Wbrew temu co mówią niektórzy eksperci rządowi, wzrost płacy minimalnej ma znaczący wpływ na ceny w gospodarce. Każde 10% wzrostu PM powoduje ok. 0,3% wzrostu w kolejnym roku, a skumulowany paroletni efekt może wynieść do 1,5%. Należy też pamiętać o cenach żywności, które będą rosnąć najsilniej, ok. 1% w ciągu najbliższego roku od wprowadzeniu nowej stawki PM. Jeżeli PIS wygra nadchodzące wybory, a wszystko na to wskazuje, PM wzrośnie o 15,6% w 2020, a o 33,3% w 2021. Nie trudno policzyć, że żywność tylko z tego powodu zdrożeje rocznie o ok. 1,5% i o ponad 3% w ciągu 2 lat.
Literatura:
[1] Draca, M., Van Reenen, J., Machin, S., The impact of the national minimum wage on profits and prices : report for the Low Pay Commission, Feb 2005;
[2] Harasztosi, P., Lindner, A., Who Pays for the Minimum Wage?, Mar 2017;
[3] https://www.money.pl/gospodarka/nowy-koszyk-zakupowy-gus-namieszal-w-inflacji-w-centrum-uwagi-zywnosc-i-prad-6359644078073985a.html;
[4] Lemos, S., A Survey Of The Effects Of The Minimum Wage On Prices, May 2006.



Brak komentarzy:
Prześlij komentarz