Dzisiejszy artykuł odwołuje się do wszystkich poprzednich części serii "Jak powstają cykle?" Poszukujemy uogólnionych czynników wpływających na ruchy cen akcji i wykorzystamy do tego wiedzę z poprzednich artykułów.
W pierwszej części artykułu "Jak powstają cykle?" pojawiał się często termin "preferencja" i "niepewność". Niepewność była wówczas rozumiana jako niezdecydowanie (a nie jako ryzyko). Należy zwrócić uwagę, iż pomimo związanego z tymi terminami subiektywizmu, ani "preferencja", ani "niepewność" nie niosą ze sobą zabarwienia emocjonalnego. Wprawdzie niezdecydowanie może wynikać ze sprzecznych emocji, ale równie dobrze z braku lub sprzeczności informacji (chyba że tymi informacjami są emocje).
Z drugiej strony od trzeciej części niniejszego cyklu przewija się wątek emocjonalny, gdzie chciwość i strach motywują do działania. Strachu nie należy mieszać z niepewnością. Strach jest lustrzanym odbiciem chciwości. Chciwość i strach są niemal tym samym. Anthony de Mello w książce "Przebudzenie" stwierdza, że pożądanie wynika w rzeczywistości ze strachu. Chciwość jest więc wtórna w stosunku do strachu. Jeśli czegoś (emocjonalnie) pragniemy, to prawdopodobnie dlatego, że się porównujemy z innymi. Jeśli czegoś nie posiadamy, co inni posiadają, a tego pragniemy, to czujemy się gorsi, co wywołuje lęk. A to jest źródłem chciwości. Ktoś powie: no jakże, przecież nauka ekonomii nie istniałaby, gdyby nikt nie chciał więcej niż ma. To prawda. Są wprowadzone do ekonomii pewne postulaty, na przykład, że im większy budżet, tym lepiej. Są też dobra nazywane dobrami pożądanymi - to te, które chcemy, czyli preferujemy. Jednak zwykłym ludziom trudno odróżnić tzw. preferencje od pożądania czegoś. Ekonomia mówiąc o preferencjach, stanowi jedynie o wyborze czegoś zamiast czegoś innego, szerzej - o wyborze ilości danego dobra względem ilości drugiego dobra. Celem jest maksymalizowanie użyteczności (i jednocześnie to jest definicja racjonalności). Nie mówi w ogóle o emocjach (a pożądanie to emocja). Dobro pożądane to tylko nazwa, nic więcej, wręcz myląca. Lepiej mówić o dobrach preferowanych i niepreferowanych. Ekonomia mówi o dążeniu jednostki do szczęścia, ale to szczęście może być opacznie rozumiane.
Świetne zrozumienie tej różnicy przychodzi po przeczytaniu "Przebudzenia". W jednym fragmencie de Mello odnosi się do czytelnika:
"Sądziłeś, ze szczęście to ekscytacja i dreszcze. Nieprawda, one tylko powodują depresję. Czy nikt ci o tym nie mówił? Jesteś podekscytowany, dobrze, ale właśnie torujesz sobie drogę do następnej depresji. Przy okazji w ten sposób pielęgnujesz kryjący się w tobie lęk."Przychodzi tu niemal natychmiastowe skojarzenie z wahadłem, którego jeden silny ruch nieuchronnie prowadzi do ruchu w przeciwnym kierunku.
Gracze giełdowi, którzy szukają wrażeń, szybko wypadają z gry. W takim tonie wyraża się A. Elder (z zawodu psychiatra) w książce "Zawód-inwestor giełdowy". Podkreśla to również B. Graham w "Inteligentnym inwestorze". Często słyszy się też o maklerach, którzy dążą do szybkich pieniędzy i szybkiej kariery, lecz żyją w tak dużym napięciu, że po paru latach kompletnie wypalają się.
Paradoks polega na tym, że emocje mogą stać się również dobrem(!) Formalnie jednostka może wybierać tyle i tyle chciwości, tyle i tyle strachu. Brzmi to niedorzecznie, ale z ekonomicznego punktu widzenia nie ma przeszkód. Żywym przykładem mogą być aktorzy filmowi, którzy wywołują u siebie różnorakie stany emocjonalne. Wiedzą oni dobrze, że nie mogą to być zbyt słabe stany, żeby ich rola nie była zbyt "płaska", ale też nie mogą być skrajne, bo prowadzi to do przesady. To czy są to rzeczywiście jakieś emocje, czy tylko udawanie, pozostawiam na boku.
Problem polega na tym, że silne emocje prowadzą bardzo często do popełniania błędów przy różnych decyzjach. Wynika z tego, że jednostka dążąca do silnych emocji preferuje popełniać błędy. Oczywiście popełnianie błędów jest efektywne, gdy prowadzi do uczenia się czegoś. Ale w tym przypadku celem nie jest uczenie się, ale właśnie samo popełnianie błędów, co staje się coraz bardziej niedorzeczne. Co więcej, popełnianie błędów w niektórych sytuacjach musi prowadzić do nieracjonalności. Załóżmy, że człowiek jest pod wpływem silnej emocji i podejmuje jakąś decyzje, ale wiadomo jednocześnie, że gdyby tych emocji nie było, podjąłby inną decyzję. Emocje nie wpływają na obiektywną sytuację, w jakiej znajduje się ta osoba, a jednak zmienia ona preferencje tylko w zależności od tego, czy emocje nią rządzą czy nie. Oznacza to niespójność preferencji, wręcz nielogiczność - co jest właśnie błędem - a więc brak racjonalności.
Ale i z tej opresji można jakoś wyjść. Ten nieracjonalny człowiek powie po prostu, że on preferuje być nieracjonalnym... W sumie czemu nie, tylko pytanie, czy rzeczywiście nie staje się on wtedy racjonalny. Można więc zadać pytanie czy zachodzi następujące paradoksalne twierdzenie:
jeśli ktoś preferuje być nieracjonalny, to zawsze będzie racjonalny.
Gdyby to twierdzenie było prawdziwe, prowadziłoby do niezłego zamieszania. Jeśli ktoś chce być nieracjonalny, to posiada względem siebie pewną preferencje, zgodnie z którą dokonuje decyzji, a więc paradoksalnie staje się racjonalny. Jeśli jednak pragnie nieracjonalności, a staje się racjonalny, to nie spełnia swoich preferencji i staje się tym samym nieracjonalny. Ale jeśli staje się nieracjonalny, to paradoksalnie faktycznie "udaje" mu się spełnić preferencje w postaci bycia nieracjonalnym... itd.
Jak widać konieczne jest powołanie do życia człowieka ograniczenie racjonalnego. Taki człowiek jest ułamkowo racjonalny, ma jakieś preferencje, ale nie maksymalizuje do końca swojej użyteczności. Ciągle tkwi w niezdecydowanym stanie na granicy racjonalności i nieracjonalności. Ale nie jest to człowiek nieracjonalny.
Przejdźmy od jednostki do zbiorowości. W części drugiej niniejszego cyklu starałem się, wykazać, że jednostki są niejako zmuszane przez rynek do zachowania ograniczenie racjonalnego. Spróbuję to przedstawić jeszcze ściślej. Załóżmy, że każdy inwestor jest w pełni racjonalny i dyskontuje każdą ważną rynkową informację. Widzieliśmy, że prowadzi to do sytuacji, że rynek staje się zupełnie nieprzewidywalny, kolejne stopy zwrotu stają się nieskorelowane, losowe. I znów paradoks: gdyby rzeczywiście każdy inwestor reagował na każdą informację, to między innymi skrupulatnie dokonywałby operacji statystycznych. A więc testy statystyczne wykazywałyby, że nie da się przewidzieć przyszłości. Obserwując takie dane nie byłoby sensu grać na giełdzie, jeśli posiadamy awersję do ryzyka (co jest cechą w sumie rozsądną, inaczej mówilibyśmy o naiwności graczy, a to "pachnie" nieracjonalnością - taki gracz szybko wypadłby z gry, a przecież nie preferuje takiej sytuacji). No chyba, że ktoś byłby nieracjonalny, co przeczy początkowemu założeniu. A więc następuje zahamowanie handlu. A jednak handel nie ustaje. To więc już dowodzi, że inwestorzy nie są w pełni racjonalni (niezależnie od tego czy stopy faktycznie są losowe, czy nie). Są więc co najwyżej ograniczenie racjonalni.
Powyższe "co najwyżej" można usunąć. Gracze nigdy nie będą całkowicie nieracjonalni, właśnie z tego powodu, który został wyżej przytoczony - zawsze można jakoś tłumaczyć swoje zachowanie i we własnych oczach pozostawać w miarę racjonalnym.
Są książki, w których stawia się tezy, że zbiorowość uczestników rynku jest w ogóle nieracjonalna. Taką tezę spotkamy na przykład u Tony'ego Plummera w "Psychologii rynków finansowych". Plummer stwierdza, że człowiek ma dwoistą naturę. "Z jednej strony każdy ma skłonność do postępowania samodzielnego i indywidualnego, zwaną również tendencją asertywną, z drugiej zaś każdego cechuje również tendencja integracyjna, w wyniku której powstaje pragnienie przynależenia do zbiorowości. Jako członkowie zbiorowości ludzie zachowują się inaczej niż postępowaliby w pojedynkę." Przyczyna tego ma być głęboko ukryta w naturze; w przyrodzie wszystko ma być wzajemnie uwarunkowane. "Jak wykazał Erich Jantsch [The Self-Organising Universe, Pergamon, Oxford 1980], wychodząc od ustaleń fizyki kwantowej, cała przyroda składa się z wielopoziomowych struktur. Każdy poziom w tej hierarchii jest w stanie organizować niższe poziomy i wykorzystywać je dla swoich celów. W konsekwencji, każdy poziom posiada zdolność zachowywania własnej tożsamości, pomimo zmian swoich indywidualnych składników."
Ludzie więc tworzą zbiorowość, która stanowi nową jakość, nowy organizm, posiada własny "umysł", zdolność do samoorganizacji. "Istotną cechą każdego systemu posiadającego zdolność organizowania się - niezależnie od tego, czy będzie to zbiorowość, czy organizm żywy - jest fakt jego oscylowania w czasie przekazywania energii i informacji. Oscylacje te kształtują cykl życia zbiorowości: narodziny, dojrzałość i śmierć.
"Zbiorowość powstaje w wyniku pewnej zmiany wywołanej przez określoną informację oraz dzięki swej zdolności do zorganizowanej reakcji na tę zmianę." "Podczas fazy rozwoju zbiorowość wykazuje pełną zdolność do zachowania swojej integralności, nawet w obliczu nieprzyjaznego otoczenia."
"W okresie swej dojrzałości zbiorowość zaczyna jednak interesować się głównie własną egzystencją, przez co staje się mało elastyczna. Zdobywa poczucie pewności siebie, pławi się w blasku swych osiągnięć i dąży do kontrolowania twórczych poczynań swoich członków."
"W końcu okazuje się, że na skutek owej sztywności struktury zbiorowość nie jest już w stanie przystosowywać się do zmian otoczenia. Oczekiwania zbiorowości nie zmieniają się i w coraz większym stopniu okazują się rozbieżne z rzeczywistością. Wówczas zaczyna się rozpad, którego oznakami są wewnętrzne spory (...) W końcu przychodzi wstrząs, który doprowadza do całkowitego rozpadu zbiorowości. Jej cykl życiowy w ten sposób domyka się, a należące do niej jednostki mogą stać się członkami innych zbiorowości. A zatem mamy tu do czynienia z ciągłym procesem odradzania się, w którym po śmierci przychodzą narodziny." (Op. cit. T. Plummer, Psychologia rynków finansowych. U źródeł analizy technicznej, s. 10, 29-31.)
Pod względem nauki o kształtowaniu się zbiorowości i złożonych struktur, warto przeczytać tę książkę. Ale czy to rzeczywiście można przenieść na ruchy akcji? Przede wszystkim należy zauważyć, że zbiorowość jako pewna zorganizowana struktura tworzy się dlatego, że siła (użyteczność) zbiorowości jest wyższa niż siła (użyteczność) sumy jednostek ją tworzących. Pod tym względem rzeczywiście rynek zdobywa siłę, kształtuje się trend. To jest to, o czym pisałem w drugiej części cyklu, że inwestorzy niejako sami się racjonalizują. Aby utrzymać organizm przy życiu komórka musi współpracować z innymi komórkami.
Jednak istnieje tu maleńka różnica, która sporo zmienia. Ta komórka, która częściowo tworzy organizm komunikuje się z innymi komórkami i dokładnie "wie", co zrobią inne. Jednocześnie sama jest od nich zależna. W społeczeństwie też od siebie zależymy. Kiedy idę do sklepu, wiem mniej więcej co zastanę i łatwo mogę przewidzieć, jak zachowa się wobec mnie ekspedient. On też łatwo może przewidzieć, co zrobię, to znaczy, że coś kupię, podejdę do kasy i wypłacę pieniądze. Społeczeństwo tworzymy, aby zwiększyć globalną użyteczność, ale jest to możliwe tylko wtedy, gdy następuje pewna synchronizacja pomiędzy jednostkami. Synchronizacja wiąże się z możliwością przewidywania tego, co zrobi druga jednostka.
A jak to jest na rynku kapitałowym? To rzeczywistość, w której jeden chce przechytrzyć drugiego. Oczywiście istnieją małe społeczności, które faktycznie sobie próbują pomóc, dostarczając różnych informacji (przykładem są fora internetowe). Ale ze względu na elektroniczną więź, siła tych społeczności jest słaba i nie ma (raczej) wpływu na ceny aktywów. W przeciwieństwie do faktycznych zorganizowanych zbiorowości, zbiorowość rynkowa jest niepewna tego, co zrobią jej członkowie.
Plummer stwierdza na początku, że ludzie mają w sobie sprzeczne tendencje do zachowania indywidualizmu i konformizmu. Można się w pełni z tym zgodzić. Ale konformizm czy inaczej tendencje integracyjne nie mogą przyćmiewać - jeśli chodzi o graczy giełdowych - tendencji asertywnych. Należy więc raczej mówić o kombinacji obydwu czynników.
Dlaczego więc trend się ustala? Pomijając czynniki fundamentalne, ludzie zachowują się podobnie, stosują podobne heurystyki, przeżywają podobne emocje, ponieważ są podobnie skonstruowani. Niektórzy szybciej się dostosowują do sytuacji na rynku, inni wolniej. Kiedy zacznie się ruch w danym kierunku, to ci szybsi będą znowu spekulować kolejny wzrost, a wolniejsi znowu po nich. W ekonomii wymieniane są dwa rodzaje okoliczności, gdy popyt rośnie, gdy cena rośnie. W pierwszym przypadku mówi się o tzw.
popycie niefunkcjonalnym, który wynika z oddziaływania tzw. efektów zewnętrznych na użyteczność. Oznacza to, że użyteczność danego dobra może się zmieniać w zależności od zachowania się innych konsumentów. Jednym z zachowań nabywców jest wtedy efekt owczego pędu, który oznacza, iż popyt na dane dobro wzrasta dlatego, że inni konsumują to dobro. W drugim przypadku mówi się o tzw. popycie spekulacyjnym, który wiąże się z oczekiwaniami co kształtowania się cen w przyszłości. [R. Milewski, Podstawy ekonomii, W-wa 2002, s. 99]. Często ludzie mylą efekt owczego pędu z popytem spekulacyjnym. Pomiędzy nimi jest jednak znacząca różnica: efekt owczego pędu jest zjawiskiem emocjonalnym, zachowaniem co najwyżej ograniczenie racjonalnym; popyt spekulacyjny jest zachowaniem wykalkulowanym i może być całkowicie racjonalny. Łatwo się domyślić, że nie jest możliwe odróżnić jeden typ od drugiego, nie tylko na giełdzie. Każdy nabywca może odpowiedzieć, że to kupno było wykalkulowane, oszukując nie tylko pytającego, lecz także samego siebie.
Teraz możemy połączyć, to o czym powiedzieliśmy. Mamy już racjonalny czynnik w postaci niepewności, ograniczenie racjonalny czynnik w postaci chciwości (strachu). Każdy z tych czynników odniesiemy do zbiorowości rynku.
Na początku naszą giełdową przestrzeń fazową będą tworzyć dwie zmienne: na osi poziomej chciwość (po stronie ujemnej - strach) oraz na osi pionowej niepewność. Dostaniemy ten sam obraz cyklu granicznego, który dotyczył wahadła.

Na rynku panują równoliczne grupy A (popyt), B (0) i C (podaż). Coś sprawia, że kurs idzie w górę. Jest to impuls dla grupy B, aby rozpocząć efekt owczego pędu bądź popyt spekulacyjny. Niech "chciwość" będzie utożsamiona z zachowaniem grupy B. Zatem z punktu, w którym oś chciwości jest równa zeru, a oś niepewności jest maksymalna, B przesuwa się w kierunku wzrostu chciwości, co powoduje spadek niepewności. Gracze stopniowo zmieniają swoje preferencje, dostosowując je do sytuacji na rynku. Zauważmy, że zmieniają je pod wpływem emocji. W końcu chciwość jest tak wielka (stopa zwrotu też), że przyćmiewa całkowicie niepewność, która równa się 0. Ale zaraz potem niepewność znowu wzrasta, lecz w kierunku przeciwnym, co powoduje, że chciwość maleje. Stopa zwrotu ciągle jest dodatnia, ale spada. W końcu niepewność znowu osiąga max, a chciwość spada do zera. Jest to moment, gdy chciwość = strach, a stopa zwrotu jest zerowa. Od tej chwili następują spadki na giełdzie, a niepewność maleje. W końcu strach jest maksymalny i niepewność zerowa. Następnie ujemna stopa zwrotu maleje, a niepewność wzrasta. W końcu strach znów zrównuje się z chciwością, a stopa zwrotu powraca do zera. Cykl zaczyna się od początku.
Jeśli ten cykl graniczny umieścimy w wymiarze czasowym, to powstanie spirala w trzech wymiarach. Z punktu widzenia jednej ze zmiennych, na przykład chciwości, dostaniemy szereg czasowy, którego wykres jest po prostu sinusoidą:

Uważny czytelnik zauważył, że zrównaliśmy poziom chciwości ze stopą zwrotu. Inaczej mówiąc poziom chciwości utożsamiamy z wielkością zmiany kapitału na rynku. Dlaczego? Ponieważ poziom chciwości jest proporcjonalny do oczekiwanej stopy zwrotu przez uśrednionego gracza. Im większą oczekuje stopę zwrotu, tym (chętniej) więcej włoży kapitału w inwestycję.
Chciwość możemy również potraktować nie jako stopę zwrotu, ale jako warunkową oczekiwaną stopę zwrotu (warunkową wartość oczekiwaną stopy zwrotu). Wtedy model staje się uogólnieniem modelu rynku efektywnego - dla rynku efektywnego chciwość = strach = 0 (brak emocji, pełna racjonalność). Jedynie panuje maksymalna niepewność, a więc warunkowa oczekiwana stopa zwrotu = 0.
Gdyby rzeczywiście tak przyjąć, to taki model byłby wystarczający. Jednak chcemy stworzyć model z rzeczywistymi zmianami, a nie tylko oczekiwanymi. Jeśli jednostki są ułamkowo racjonalne, to z pewnością nie będą się zachowywać jak nieracjonalna zbiorowość w sensie Plummera. Będą starać się wykorzystywać każdą możliwość, by zarobić, ale jednocześnie będą pod wpływem zachowań innych graczy. Gdyby byli taką Plummerowską zbiorowością, szybko zdyskontowaliby wiedzę o "narodzinach", "dojrzałości" i "śmierci" zbiorowości. Coś takiego jest iluzją. Jeśli już mówić o istnieniu pewnej zorganizowanej struktury, to nie w sferze realnej, lecz abstrakcyjnej (istnieje niewidzialna nić połączeń pomiędzy jednostkami oparta na emocjach i heurystykach). Umożliwi to model chaotyczny. Założymy, że ruch cen akcji odbywa się w czasie ciągłym. Wtedy musimy uwzględnić trzecią zmienną w przestrzeni fazowej, aby możliwe było wywołanie chaosu.
Niech trzecią zmienną stanowi czynnik fundamentalny. Wcześniej utożsamialiśmy ten czynnik z grupą D. W zależności od wielkości grupy D, wywoływała ona większy lub mniejszy impuls, który znowu stawał się efektem motyla dla grupy B. Czynnik fundamentalny możemy, podobnie jak to uczyniliśmy z "chciwością", określić jako zmianę wartości zmiany kapitału, czyli zmianę stopy zwrotu (dynamika kapitału zależy od ogólnej koniunktury gospodarczej). Analogią jest tu prędkość i przyspieszenie. Prędkość to zmiana drogi w czasie, przyspieszenie to zmiana prędkości w czasie, czyli zmiana tej zmiany drogi w czasie.
Jeśli więc trzy podukłady - zmiana wartości kapitału, zmiana wartości tej zmiany oraz niepewność nie będą ze sobą synchronizować, pojawi się ruch chaotyczny.
Nie wiadomo jednak, jak taki atraktor chaotyczny wygląda. Może przypomina dziwny atraktor wirnika? Poniżej przedstawiono dwa przykłady chaotycznych portretów fazowych (projekcji atraktora na wybrane osie współrzędnych) dla drgań wirnika z dwóch różnych perspektyw i odpowiadający przebieg czasowy jednej ze zmiennych.

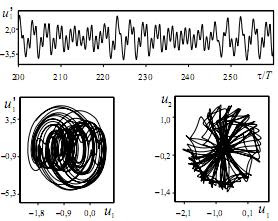
[Rysunki wzięte z U. Ferdek, Wpływ zderzeń na drgania poprzeczne i skrętne wirników, Czasopismo techniczne, 1-M/2008, s. 93].
W następnym, czyli ostatnim odcinku z serii "Jak powstają cykle?" poruszymy meritum sprawy, tj. istnienie cykliczności i podcykliczności trajektorii w układach chaotycznych.




































