Jak ustalić cenę sprzedaży i marżę?

Jesteś przedsiębiorcą, który wchodzi na rynek z nowym, ciekawym produktem lub usługą. Zastanawiasz się jednak po ile wycenić produkt i jaką marżę wyznaczyć. To jest fundamentalne pytanie z punktu widzenia wyceny projektów. Projekt najczęściej wycenia się metodą zdyskontowanych przepływów pieniężnych (NPV), ale czy samą cenę jednostkową można w ten sposób ustalić? Nie, bo - pomijając problematykę stopy dyskontowej - w liczniku NPV znajduje się już taki element jak przychód, który składa się z ceny i ilości sprzedanej produkcji.

Jeżeli mamy przeciętnego przedsiębiorcę, to zapewne nie będzie się zbyt długo nad tym zastanawiał - po prostu pochodzi po ulicach, przejrzy anonse, czyli sprawdzi jaka jest cena rynkowa i biorąc czy to średnią, czy średnią + odchylenie standardowe (jeśli uważa, że jego produkt jest wart więcej niż tylko średnia), wyceni swój produkt. Następnie skalkuluje roczne koszty i na ich podstawie sprawdzi czy inwestycja jest opłacalna. Obliczenie marży nie będzie dla niego problemem. Taki przedsiębiorca nie musi studiować ekonomii, aby oszacować cenę i rentowność sprzedaży.

Ale powyższy wywód jest tautologią: skoro z założenia ktoś jest przeciętnym przedsiębiorcą, to nie może wyceniać dobra więcej niż to robi rynek. Trudniej mają ci nieprzeciętni, którzy mają zamiar wejść na rynek z nowym, innowacyjnym produktem albo produktem o lepszej jakości. Z pomocą przychodzi tu mikroekonomia.

Opiszę zagadnienie w 5 punktach.

1) Przedsięwzięcie jest opłacalne, gdy przychody (iloczyn ilości dobra i jego ceny) minus koszty są większe od zera. Oznaczając p - cena danego dobra, y - ilość sprzedawanego dobra, c - koszty poniesione na wytworzenie i sprzedanie dobra w danym okresie, możemy zapisać:

gdzie AC (average cost) - koszt średni albo przeciętny.

Widzimy więc, że podstawową zasadą opłacalności inwestycji jest to, aby cena produktu czy usługi była większa od kosztu przeciętnego. Pierwsze co trzeba zrobić, to oszacować mniej więcej koszty  i podzielić przez ilość dobra, jaką prognozujmy sprzedać w danym okresie. Trzeba tu zauważyć, że ten model odnosi się do konkretnego okresu czasu. Załóżmy, że początkowe nakłady inwestycyjne ponoszone są w 2016 r., a sprzedaż i koszty uzyskanego przychodu, tylko w roku 2017. Oznacza to, że za c podstawiamy tylko koszty z roku 2017. Właściwie można powiedzieć, że model dokładnie odzwierciedla zasady księgowości, jak zasada współmierności kosztów i przychodów oraz zasada memoriałowa. Musimy więc brać pod uwagę także amortyzację - gdyż jest to często koszt rozłożony w czasie. Ciekawe zagadnienie pojawia się, gdy zastanawiamy się nad kosztami czysto ekonomicznymi, jak koszt czasu i ryzyka. Uwzględniać czy nie uwzględniać? W tej materii musimy się spytać o jaką opłacalność inwestycji chodzi? Księgową, pieniężną, a może czysto ekonomiczną? Jeśli badamy opłacalność pieniężną, to nie mamy już do czynienia z kosztami, ale wydatkami, czyli badamy przepływy pieniężne. Jeśli natomiast badamy przedsięwzięcie bardzo szeroko, czyli jego efektywność ekonomiczną, to bierzemy też koszt czasu, ponoszonego ryzyka i efekty zewnętrzne (jak np. zanieczyszczenie środowiska, hałas i wszystko inne co obniża dobrobyt społeczny). W konsekwencji zysk ekonomiczny może być zerowy albo bardzo bliski zera. Mimo to księgowo albo pieniężnie inwestycja może być bardzo opłacalna. Na pewno warto sobie zrobić taką ocenę projektu z 3 różnych płaszczyzn. Trzeba jednak pamiętać, że rozpatrywane koszty (albo wydatki w formie przepływów pieniężnych) dotyczą tylko tego jednego dobra - jeśli produkujemy 2 różne dobra, to koszty dotyczące 2-go dobra muszą zostać odpowiednio odjęte.

2) Ten sam model zapiszmy dokładniej, tzn. jako równanie przychody - koszty = zysk i od razu przekształćmy

gdzie z - zysk, M - marża netto (rentowność sprzedaży) równa zysk/przychody.

Otrzymaliśmy ciekawy wzór na cenę produktu: jest ona równa kosztowi przeciętnemu podzielonemu przez (1 - marża netto).

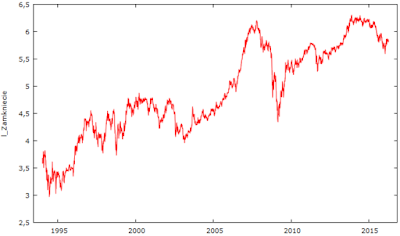
Cenę warunkuje więc marża, ale ile powinna ona wynieść? Można to rozwiązać na co najmniej 2 sposoby. Po pierwsze można skorzystać z danych historycznych. Najłatwiej dostępne są dane dla rynku amerykańskiego, np. dla S&P 500. Poniżej zamieszczone dane zasięgnąłem ze strony http://www.multpl.com/. Aby uzyskać marżę, inaczej wskaźnik ROS (return on sales), podzieliłem wskaźnik cena/przychód przez cena/zysk dla lat 2000-2016.

Średnia marża = 6,87%, dominanta = ok. 7,7%.

Ta zgrubna metoda może i jest dość dobrym punktem wyjścia, jednak dla przedsiębiorcy z dużym potencjałem wzrostu sprzedaży, może być nieprzydatna. Dlatego dobrze też użyć drugiej metody. Aby ją zastosować, potrzebny jest trzeci punkt analizy.


3) Dotychczas nie zakładaliśmy, że przedsiębiorca chce osiągnąć jak najwyższy zysk. Dopiero to założenie pozwoli wyznaczyć cenę i marżę. Z maksymalizacją funkcji zysku wiąże się wiele problemów. Pierwsze to oczywiście takie, względem czego maksymalizować zysk? Mamy przecież 3 zmienne: cenę, ilość dobra i koszty. Moglibyśmy próbować maksymalizować zysk względem każdej zmiennej. Powiedzmy, że maksymalizujemy względem ceny. Wiadomo, że cena nie może być zbyt niska, bo zarobimy mniej niż byśmy mogli, ani zbyt wysoka, bo za mało chętnych osób kupi produkt. To podejście jest ciekawe, ale musielibyśmy znać zależność funkcyjną popytu od ceny. Musielibyśmy wiedzieć, jak y zmieni się w zależności od p. Jeżeli przedsiębiorca wchodzi z nowym produktem czy usługą na rynek, to mógłby zrobić pewne badania rynkowe, ankiety itd. Ale to też kosztuje. Łatwiej zacząć od zmiennych, które dobrze znamy i którymi możemy kalibrować. Zamiast od strony popytu, zacznijmy od strony podaży - oceniamy co się stanie, gdy nieco zmienimy y. Zakładamy, że zmienne są funkcjami zależnymi od y. Dostajemy:

Zgodnie z rachunkiem różniczkowym, jeśli funkcja ma ekstremum, to warunkiem koniecznym jest, aby pierwsza pochodna po y równała się 0. Od razu też przekształćmy:

gdzie MC (marginal cost) to koszt krańcowy, który mówi ile zmieni się koszt całkowity (ale tylko ten związany z dobrem y) na skutek niewielkiej zmiany w produkcji dobra (lub dostarczeniu usługi). Ponieważ produkt ze swojej natury jest liczony w jednostkach naturalnych, to ta niewielka zmiana produkcji będzie po prostu oznaczać 1 dodatkową jednostkę produktu. Jeżeli produkujemy o 1 jednostkę więcej, to być może potrzebujemy zużyć do tego więcej materiału, zatrudnić dodatkowego człowieka itp. Suma tych nowych kosztów to właśnie MC.
 
Jeżeli cena p zależy od y, to zgodnie z twierdzeniami na pochodnych - przekształcając przedostatnie równanie - dostaniemy:

Ostatnim elementem poszukiwania maksimum zysku byłoby sprawdzenie czy druga pochodna funkcji zysku jest ujemna, tzn. czy nachylenie tej funkcji spada, gdy wyprodukujemy nieco więcej dobra. Żeby zysk osiągnął maksimum, to zanim go osiągnie, musi rosnąć coraz wolniej. Okazuje, że przy całkiem naturalnych założeniach, tak właśnie się dzieje. Dowód opisałem w Dodatku*.

I to już koniec matematyki wyższej. Reszta to zwykłe przekształcenie:

W nawiasie kwadratowym dostaliśmy coś interesującego: procentową zmianę ceny na skutek procentowej zmiany ilości dobra. Jak wyżej stwierdziłem interesuje nas mała zmiana y. Powiedzmy, że w przybliżeniu:

Możemy również spokojnie pozwolić sobie na zapis:

 Wtedy dostaniemy:

gdzie r = r% / y% = r% / 1%.

Takie rozpatrywanie sprawy jest kłopotliwe. Czy zwiększenie / zmniejszenie produkcji wywoła w nas motywację do zmian ceny? Jeśli trafiamy na jakieś przeszkody w produkcji, tak że nasze zasoby stają się ograniczone, to z jednej strony chcielibyśmy podnieść cenę, aby skompensować mniejsze zyski (jeżeli podaż dobra spada, to jego cena rośnie).  Ale z drugiej strony, jeżeli mniej produkujemy, to koszty spadają, co ogranicza spadek zysków.
Lub na odwrót - jeśli chcemy więcej sprzedać, to powinniśmy obniżyć cenę. Ale jeśli więcej produkujemy, to podnosimy też koszty, które ograniczają zyski.
W konsekwencji cena może w ogóle się nie zmienić albo zmienić się nieznacząco. W takiej sytuacji cena będzie równa kosztowi krańcowemu: p = MC. Cena stanowiłaby dodatkowy koszt, który powstaje w wyniku zwiększenia produkcji o jednostkę.


4) W końcu połączmy wzór na cenę z punktu (2) z ostatnim wzorem na cenę z punktu (3) i stąd odnajdziemy wzór na M:

Odpowiedź na tytułowe pytanie znaleźliśmy. Newralgicznym punktem pozostaje r. Rozwiązemy ten problem w p. 5.


5) Przy analizie rentowności dobrym pomysłem jest wykorzystanie ROE lub ROA, których odwrotność można interpretować jako okres, po jakim zwraca się inwestycja (pokazuje bowiem ile jednostek zysku mieści się w kapitale, przez który się dzieli, a liczba tych jednostek odpowiada liczbie okresów finansowych). Np. jeżeli ROE = 10%, to znaczy, że inwestycja zwróci się po 10 latach, a jeżeli 20%, to po 5 latach (zysk po tylu latach zwróci zainwestowany kapitał). Łatwo zauważyć też, że

gdzie WK - wartość księgowa kapitału własnego, którą znamy. Stąd:

Podstawiamy ten wzór do wzoru w p. 4:

Rozwiązujemy to równanie względem p:

5a)

Wykorzystując wzór z p. 3, wiemy, że cena = MC / (1+r) i podstawiając go do powyższego:

Rozwiązujemy to równanie względem r:

5b)

Zatem otrzymaliśmy wpływ zmiany produkcji na zmianę ceny lub na odwrót. Podstawiamy prawą stronę (5b) do (5a) i rozwiązujemy względem p:

5c)

Zauważmy, że pozbyliśmy się ze wzoru (5c) zarówno kosztu krańcowego (MC) jak i marży (M). Otrzymaliśmy bardzo prosty wzór, ponieważ koszt przeciętny (tj. koszty całkowite podzielone na wielkość produkcji danego roku) powinniśmy potrafić oszacować, kapitał własny (WK) znamy, a ROE szacujemy w ten sposób, że odpowiadamy sobie na pytanie, po ilu latach najpóźniej chcemy, aby w całości zwrócił się WK.

Jeżeli inwestycję finansujemy także kapitałem obcym, to dla szerszej perspektywy, warto użyć ROA w miejsce ROE:

5d)

gdzie 

ROA = oczekiwany zysk w danym roku /Aktywa,

A - Zainwestowane aktywa, tj. kapitał własny + dług. 

Oczywiście jest to to samo, ale tym razem szacujemy po ilu najpóźniej latach spodziewamy się, że zarówno dług jak i kapitał własny zwróci się w całości. Jednakże, jeżeli znamy ROE, to nie jest nawet  konieczne:

Przykład:

Chcemy oszacować cenę produktu. Robimy to w trzech etapach:

Etap 1. Szacujemy, że całkowite koszty, jakie poniesiemy w tym roku to ok. 50 000. Chcielibyśmy sprzedać średnio 10 sztuk towaru dziennie, czyli ok. 3650 w roku. Cały kapitał własny, jaki zainwestowaliśmy to 30 000 (reszta to kredyty). Chcielibyśmy, żeby ten kapitał zwrócił się po 3 latach. To znaczy, że ROE = 1/3 = 33%. Podstawiamy dane do (5c):

p = 50000 / 3650 + 0,33*30000 / 3650 = 16,4.

Etap 2. Powiedzmy, że nie znamy ROE. Szacujemy, że cały kapitał (dług + kapitał własny) zwróci się po 4 latach. Stąd ROA = 1/4 = 25%. Kredyty = 25 000, stąd A = 55 000. Wobec tego podstawiamy do (5d):

p = 50000 / 3650 + 0,25*55000 / 3650 = 17,5.

Etap 3. Wyciągamy średnią: (16,4 + 17,5)/2 = 16,95.

W ten sposób ustalamy cenę produktu na poziomie ok. 17. Oczywiście zamiast średniej możemy ustalić dowolną wartość w przedziale 16-17. 

*DODATEK
Warunek konieczny i wystarczający dla maksymalnego zysku może zostać spełniony dla wielu modeli zarówno liniowych, jak i nieliniowych. Zanim podzielimy problem na te dwa przypadki, to spostrzeżemy jedną rzecz. Mianowicie, całkiem rozsądne jest, że gdy trochę więcej produkujemy, to cenę produktu obniżamy: jeżeli jestem zmotywowany, by sprzedać więcej dobra, to powinienem obniżyć jego cenę (czyli pierwsza pochodna ceny jest ujemna).

(1) Nieliniowe modele.
Mogę tak robić, dopóki koszty mi nie przeszkadzają. Jednak z czasem koszty mogą mocno ograniczać moje możliwości. Im większa skala produkcji, tym więcej problemów, potrzebne są nowe budynki, nowi menedżerowie, a ponadto jeśli zależy mi na zatrudnianiu nowych pracowników, to popyt na pracę będzie zmuszał do podnoszenia wynagrodzenia. To wszystko razem będzie generowało coraz wyższe koszty krańcowe (gdyby tego skumulowanego efektu nie było, koszty całkowite by rosły, ale koszty krańcowe stałyby w miejscu).

Prowadzi to do wniosku, że z jednej strony cena na skutek zmian produkcji powinna spadać coraz wolniej (a być może nawet od jakiegoś punktu zacząć rosnąć) i zachowywać się np. jak funkcja p(y) = 10*y^(-1/2):

Wtedy jej pierwsza pochodna będzie funkcją -5*y^(-3/2):

Druga pochodna ceny po y ma wtedy postać 15/(2 y^(5/2)):

Widać, że druga pochodna jest dodatnia. Ma to istotne znaczenie dla znalezienia maksimum zysku.

Z drugiej strony - zgodnie z powyższą analizą - koszty całkowite będą rosły coraz szybciej, np. niech c = 2y^(3/2):

A wtedy koszty krańcowe muszą rosnąć. Dla przykładowej funkcji c dostaniemy MC(y) =  3y^(1/2):

Druga pochodna kosztów c po y ma postać 3/(2y^0.5):

Teraz łatwo zobaczyć, że istnieje maksimum zysku.
Pokażmy to rachunkowo, po kolei:

Pierwsza pochodna po y:

gdzie MP(y) to krańcowy zysk (marginal profit). Warunkiem koniecznym maksimum jest aby:

Dla naszego przykładu dostaniemy:

Ale przecież na początku podałem postać funkcji p(y). Musi zostać spełniony układ równań:

Punkt ten wyznacza pewne ekstremum, ale nie wiadomo czy minimum czy maksimum.
Dla ułatwienia oznaczmy:

Warunkiem wystarczającym istnienia maksimum jest, aby druga pochodna funkcji zysku po y była mniejsza od zera:

Dla wybranego wcześniej przykładu dostaniemy:

Nierówność ta zostanie spełniona dla każdego y > 0. Stąd warunek wystarczający maksimum został spełniony.

(2) Modele liniowe.
Załóżmy prostszą sytuację, że po pierwsze cena spada liniowo, np. p = 14 - 3y. W tej sytuacji s = -3 oraz druga pochodna = 0. Po drugie, że koszty rosną liniowo, np. c = 2y. Wtedy MC = 2, ale druga pochodna = 0. Wtedy warunek konieczny to p - 3y = 2. Znów rozwiązujemy układ równań:

Warunek wystarczający to 2*(-3) + 0 < 0 jest zawsze spełniony, więc istnieje maksimum.

Chociaż warunek wystarczający zostanie spełniony zawsze dla liniowych modeli (jeśli tylko r < 0), to z warunkiem koniecznym jest już trudniej. Np. jeśli c = 20y oraz p = 14 - 3y, to y = -1, a więc produkcja powinna wynieść co najwyżej 0, czyli najbardziej opłacalne byłoby nie prowadzić działalności.

Czym się różni pamięć długoterminowa od krótkoterminowej?

Gdy myślimy o procesach biologicznych, intuicyjnie rozumiemy co oznacza pamięć krótkoterminowa a co długoterminowa. Ale w procesach finansowych sprawa się komplikuje. Przykładem procesu z krótką pamięcią jest AR(p). Jednak rząd p = 1 nie oznacza wcale, że całkowita pamięć działa tylko 1 krok naprzód. Na przykład wygenerujmy następujący skorelowany gaussowski proces z 1000 obserwacji:

Sprowadzając go do stacjonarności (czyli biorąc pierwsze różnice) otrzymamy zwykły AR(1) ze współczynnikiem autoregresji 0.6 (czyli jest to ruch Browna z autokorelacją 1 rzędu). Dostaniemy dla niego funkcję autokorelacji - ACF: 

Empiryczny ACF zaczyna się faktycznie od poziomu 0.6, ale w kolejnych rzędach błędnie odnajduje dodatkowe autokorelacje. ACF wskazuje, że pamięć kończy się dopiero przed 6-tą obserwacją (p-value = 0.11). Dzieje się tak, dlatego że kolejne obserwacje wpływają na siebie: jeżeli jednego dnia jest wzrost, to szansa na wzrost kolejnego dnia jest spora, ale skoro tak, to i trzeciego dnia będzie spora itd. Tak więc pozornie pierwszy dzień wpływa na trzeci, czwarty itd. To daje do myślenia. Ten efekt może być pomylony z "efektem motyla" znanym z teorii chaosu,  który będzie związany z pamięcią długoterminową, ale nie krótkoterminową.
Aby usunąć te wewnętrzne autokorelacje, stosuje się cząstkową autokorelację PACF (partial ACF).

PACF wyraźnie wskazuje, że już po 1 kroku autokorelacja znika.

Stąd PACF służy do oceny autokorelacji p-tego rzędu, a jednocześnie pozwala dobrać optymalny poziom p w modelu AR(p).

A teraz wygenerujmy proces z długą pamięcią, ale bez krótkiej, tzn. część AR(1) = 0, a więc wydawałoby się, że także autokorelacja cząstkowa nie wystąpi. Niech to będzie proces o takim przebiegu, również z 1000 obserwacjami:

Jest to ułamkowy proces ruchu Browna z wykładnikiem Hursta = 0.9, czyli jego pierwsze różnice charakteryzują się ułamkowym rzędem integracji d = 0.4 w modelu ARFIMA (krótkie opisowe wyjaśnienie ułamkowego rzędu integracji zamieściłem w Czy oczekiwane stopy zwrotu w ogóle się zmieniają?, tam też opisałem znaczenie ACF). Analizując pierwsze różnice, zacznijmy znowu od ACF:

Tym razem ACF spada o wiele wolniej i pamięć utrzymuje się jeszcze długo po 9-tej obserwacji. Następnie sprawdźmy PACF:

Autokorelacja cząstkowa zanika dopiero po 3 kroku. Sugerowałoby to, że aby wymodelować ten proces, trzeba by użyć AR(3), a właściwie ARFIMA(3, 0.4, 0) - część MA zostawiam, aby nie wprowadzać zamieszania. A jednak gdy mamy do czynienia z procesami o długiej pamięci, ta klasyczna zasada Boxa-Jenkinsa nie działa. Przecież wygenerowałem ten proces, wiedząc, że nie posiada krótkiej pamięci, którą odnajduje PACF. Żeby zauważyć, że rzeczywiście długa pamięć "myli" PACF, możemy estymować 2 modele: ten prawidłowy, tj. ARFIMA(0, 0.4, 0) oraz ARFIMA(1, 0.4, 0). Taką możliwość daje program Matrixer.

ARFIMA(0, 0.4, 0)

Dostaliśmy d = d1 = 0.448. Ocena parametru jest bliska prawdziwemu 0.4.

ARFIMA(1, 0.4, 0)

W tym przypadku część AR(1) okazuje się nieistotna statystycznie (p-value = 0.176), natomiast d = d1 = 0.388 jest istotny i bliski prawdziwemu 0.4.

Nie ma sensu zwiększać p aż do 3, skoro już 1 rząd jest nieistotny. Dlatego widać, że długa pamięć może zastąpić całkowicie autoregresję. PACF działałby tylko wtedy, gdybyśmy od początku nałożyli warunek, że d = 0, czyli po prostu estymowali zwykły AR. Wtedy istotnie powinniśmy zastosować AR(3).

Mimo iż pamięć jest rozważana w rozmaitych kontekstach, to okazuje się, że różnicę pomiędzy pamięcią krótko- a długoterminową można sformułować następująco: pamięć, w sensie ACF, krótkoterminowa zanika geometrycznie, natomiast długoterminowa - hiperbolicznie [1, 2]. Przykładem funkcji, która maleje geometrycznie jest e^(-x), a hiperbolicznie 1/(1+x). Poniższe rysunki pozwalają porównać obydwa zjawiska:

Tak więc w szeregach czasowych z długą pamięcią, ACF i PACF są nieprzydatne. ACF może błędnie sugerować niestacjonarność procesu (kolejne obserwacje korelują ze sobą, powodując nieprzypadkowe zmiany, co wywołuje ich oddalanie się od średniej), a PACF autokorelację pierwszych rzędów. Może się oczywiście zdarzyć odwrotnie - istnieć autokorelacja liniowa dalekiego rzędu, np. 7-go i jeśli nie wyłapiemy AR(7), to błędnie oszacujemy występowanie długiej pamięci. Co więcej, nawet jeśli wyłapiemy AR(7), ale nie zauważymy, że reszty modelu są (nadal) wzajemnie skorelowane, to też błędnie oszacujemy występowanie długiej pamięci. To właśnie dlatego, aby usunąć autokorelacje pomiędzy resztami (składnikami losowymi), stosuje się proces MA. Stąd podstawą jest model ARMA, ARIMA i dopiero potem ARFIMA.

Literatura:
[1] Pong S., Shackleton, M. B., Taylor, S. T., Distinguishing short and long memory volatility specifications, 2008;
[2] Jin H. J., Frechette, D. L., Fractional Integration in Agricultural Futures Price Volatilities, May 2004.

Robot ma wielkie oczy

Każdy prawdziwy inwestor rozumie, że praca sama w sobie nie jest wartością, że nie jest celem samym w sobie. Że stanowi tylko narzędzie do uzyskania dochodów. W wielu popularnych poradnikach - często pisanych przez ludzi, którzy rzeczywiście przeszli drogę od zera do milionera - przeczytamy czy wysłuchamy, że celem powinna być zawsze wolność finansowa, a nie dobra praca.

Można powiedzieć, że tak myślą inwestorzy - marzą, by ich portfele rosły same bez udziału ich wysiłku. Nie mieli by nic przeciwko temu, żeby program komputerowy (czy robot) sam optymalizował ich udziały w papierach wartościowych czy innych aktywach.

Ale coraz częściej można spotkać się z fatalistycznymi wizjami i zmartwieniami samych ekonomistów, o tym, że wkrótce roboty i sztuczna inteligencja zabiorą ludziom pracę - zarówno fizyczną jak i umysłową - i trzeba się ich bać. Dobra - gdyby tylko jacyś tam nieznani ekonomiści tak się przejmowali - to pal licho. Ale gdy słyszy się to z ust szanowanych, często nagradzanych ekonomistów - to budzi zgrozę. Dla przykładu - zacytuję http://www.businessinsider.com [1]:

"A Nobel Prize-winning economist has warned that the rise in robotics and automation could destroy millions of jobs across the world. Angus Deaton, who won the Nobel Prize last year for his work on health, wealth, and inequality, told the Financial Times he believes robots are a much greater threat to employment in the US than globalisation."

Richard B. Freeman z kolei pisze długi artykuł na ten temat i najpierw zauważa, że strach przed globalnym bezrobociem jest bezpodstawny [2]:

"From the 1930s through the 1990s, fears that technological advances would create permanent joblessness—which seemingly arise whenever unemployment persists for a long period—have proven groundless. In his 1940 State of the Union address, President Franklin Roosevelt blamed high unemployment on the nation’s failure to “[find] jobs faster than invention can take them away,” but when demand ramped up during World War II, the surplus of labor turned into a shortage. In the early 1960s, fears that automation would eliminate thousands of jobs per week led the Kennedy administration to examine the link between productivity growth and employment, but the late 1960s boom ended the automation scare. During the mid-1990s recession, some analysts proclaimed the end of work, only to see the dot-com boom raise the proportion of the adult population working to an all-time high. Employment returns when the economy recovers. And mechanization and automation have been accompanied by an improvement in the structure of jobs, with humans shifting from manual work to professional and managerial work. In the past several decades, the ratio of employment to population has increased rather than decreased. Should this time be different?"

Ale zaraz potem potwierdza, że obecna automatyzacja przechodzi w nową fazę, w której roboty zaczynają przejmować pracę umysłową:

"Pedro Domingos, a computer scientist at the University of Washington, has predicted that “tomorrow’s scientists will have armies of virtual graduate students, doing lab work, statistical analysis, literature search, and even paper-writing.”"

i za chwilę przyłącza się do litanii zagrożeń robotyzacji.

Ekonomiści budują całe modele obliczające ilu ludzi straci pracę i ilu będzie cierpieć przez sztuczną inteligencję [3].

Niewiarygodne, że nawet Bill Gates uważa, że roboty powinny zostać opodatkowane! [4]. Gates jako najbogatszy filantrop na świecie może sobie płacić podatki nawet za oddychanie, ale z lekka drażni sposób, w jaki przedstawiają to dziennikarze, nazywając taki pomysł "rewolucyjnym". Ja rozumiem, że rewolucyjnym pomysłem jest opodatkowanie przychodów. Bo nie inaczej chce Gates.

Dlaczego pomysł Gatesa nie tylko nie jest rewolucyjny, ale jest idiotyczny? Każdy kto trochę zna ekonomię wie, że postęp techniczny obniża koszty, a więc zwiększa tym samym dochody. A skoro przedsiębiorca otrzymuje wyższe dochody, to płaci wyższy podatek dochodowy. Tym samym zyskuje zarówno przedsiębiorca jak i państwo. Z tych podatków państwo może finansować zasiłki i inne potrzeby socjalne. Na tym opiera się prawdziwy rozwój gospodarczy.

Tymczasem Gates chce by robota traktować na równi z człowiekiem, czyli uważać, że robot uzyskuje jakiś dochód, od którego trzeba pobrać podatek. Co jest oczywiście fałszem, bo robot nie uzyskuje żadnego wynagrodzenia, a tylko pracodawca niejako przejmuje to wynagrodzenie (i w ten sposób obniża swoje koszty). Co oznacza, że Gates chce, aby dochody zostały podwójnie opodatkowane (a z VAT potrójnie): od przychodu z robota i od zysku brutto. A przecież zysk brutto i tak wzrósł, a więc jest podatek nie tylko od przychodu, ale jeszcze od wyższego zysku brutto.

Przykład: powiedzmy, że początkowo zysk brutto wynosi 1, a dzięki robotowi jest to 1+x = y. Jeśli podatek wynosi 0,2 zysku brutto, to bez robota podatek wynosi 0,2, a z robotem 0,2(1+x) = 0,2y. Jest to prawidłowa sytuacja, gdy państwo zyskuje dzięki robotowi dodatkowe 0,2x. Tak więc już pewna część przychodu z robota jest opodatkowana. Ale teraz dokonajmy grabieży, którą proponuje Gates: najpierw opodatkowujemy x, czyli pierwszy podatek to 0,2x. Tę część odejmujemy od zysku brutto, czyli y - 0,2x stanowi podstawę podatku dochodowego. Ponieważ y = 1+x, to podstawa wynosi 1+x - 0,2x = 1+ 0,8x. Z tego wyliczamy podatek 0,2*(1+0,8x). Tak więc gdy zsumujemy obydwa podatki, to dostaniemy 0,2x + 0,2(1+0,8x) = 0,2(x + 1 + 0,8x) = 0,2(1 + 1,8x). Jeśli x = 0, wtedy dostaniemy początkowy podatek 0,2. Ale jeśli x > 0, to zawsze dostaniemy większy całkowity podatek. Podsumujmy te 3 sytuacje:
1. gdy nie ma robota, to podatek = 0,2
2. gdy jest robot, ale jeden podatek od zysku brutto, to podatek ten wynosi 0,2(1+x)
3. gdy jest robot, ale są dwa podatki - od przychodu i zysku brutto, to podatek sumaryczny wynosi 0,2(1 + 1,8x).

I oczywiście analogicznie łatwo zauważamy, że końcowy zysk netto wynosi odpowiednio dla tych sytuacji:
1. 0,8
2. 0,8(1 + x)
3. 0,8(1 + 0,8x)

A wracając do meritum: powiedzmy, że roboty przejmą niemal całą pracę ludzi, razem z prawnikami, sędziami, księgowymi, inżynierami, lekarzami, politykami itd. No i co z tego? Czy praca sama w sobie jest świętością? Czy chodzi o to, żeby mieć pracę czy pieniądze? Jeżeli ludzie uważają, że chodzi o to, by mieć pracę, to oczywiście będzie dla nich problem. Ale to będzie problem wyłącznie psychologiczny, a nie realny, ekonomiczny. Powyżej podałem właściwie rozwiązanie. Postęp techniczny, jak np. sztuczna inteligencja zwiększa oszczędność czasu i obniża koszty, a przez to zwiększa dochody. Większe dochody oznaczają większe podatki, które można przeznaczyć dla wszystkich tych, którzy nie potrafią dostosować się do panujących warunków. W przyszłości, dzięki olbrzymiemu postępowi, państwa - jeśli nie dojdzie do kolejnej wojny światowej albo globalnej pandemii - będą posiadać ogromne z dzisiejszego punktu widzenia dochody, które będą przeznaczać na warunki socjalne, ale nikt nie będzie już tego nazywał zasiłkami, bo po prostu będzie to coś normalnego, naturalnego. Każdy będzie dostawał pieniądze od państwa na utrzymanie, a ludzie będą mieć więcej czasu na rozwój osobisty, naukę, badania, rodzinę itp. Dlatego kapitalizm przejdzie w sposób naturalny w swego rodzaju ekonomię dobrobytu. Warto zauważyć, że już dziś państwa nazywane państwami dobrobytu, wcale nie przeżywają wielkich kryzysów gospodarczych. Należy jednak pamiętać, że aby taka wizja mogła się spełnić, to wszelka pomoc socjalna nie może opierać się na zadłużaniu państwa, ale przeciwnie - tylko nadwyżka budżetu może być wykorzystana do celów socjalnych.

Dziś komputer potrafi wygrać już w pokera z najlepszymi zawodnikami. Tak więc wkrótce automaty będą mogły przejmować niektóre zadania umysłowe. Gdy roboty przejmą np. pracę polityków, to nastąpi ogromny spadek kosztów i olbrzymia oszczędność. Decyzje będą zawsze szybkie, optymalne (bo oparte na pełnej wiedzy ekonomiczno-socjologicznej), ludzie nie będą się wściekać, nie będzie protestów, strajków itd. - obniżą się koszty społeczne. Również gdyby robot był sędzią, to wydawałby zawsze najbardziej sprawiedliwe, optymalne wyroki w oparciu o całą wiedzę prawniczą. I nikt nie mógłby go posądzać o stronniczość. Oczywiście ktoś to wszystko musi kontrolować. Zawsze będą ludzie, ktorzy będą mieć pracę. Być może większość ludzi będzie musiała być informatykami lub kimś łączącym informatykę z innym zawodem. Fataliści od science-fiction zaczną oczywiście snuć obawy, co to będzie jak robot przejmie rolę informatyka. Ja im proponuję w takim razie, by od  razu podyskutowali, co tu zrobić jak Słońce się wypali.



Źródło:
[1] NOBEL ECONOMIST: 'I don’t think globalisation is anywhere near the threat that robots are'
[2] Who Owns the Robots Rules the World
[3] Seth G. Benzell, Laurence J. Kotlikoff, Guillermo LaGarda, Jeffrey D. Sachs,  Robots Are Us: Some Economics of Human Replacement, 2016. Link: http://www.nber.org/papers/w20941
[4] Bill Gates z rewolucyjnym pomysłem: Opodatkować roboty

Optymalizacja wstępnych parametrów modelu log-periodycznego

Jeżeli mamy trudności z uzyskaniem wartości krytycznej w modelu log-periodycznym, wtedy możemy spróbować użyć pewnego przekształcenia, które pokazali Filiminov i Sornette [1]. W pierwotnym modelu występowały 3 parametry liniowe: A, B, C oraz 4 parametry nieliniowe a, w, tc, d. Można model przekształcić do takiej postaci, aby uzyskać 4 parametry liniowe i 3 nieliniowe. Nieliniowość powoduje, że obliczenia są bardzo skomplikowane i program komputerowy może nie dać rady rozwiązać problemu numerycznego. Dodatkowo nieliniowość tych parametrów wywołuje quasi-periodyczność, przez co funkcja może mieć wiele punktów optymalnych.

Przypomnę, że pierwotna wersja była następująca:

(1)

Przekształcenie modelu (1) da postać:

(2)

Wzór (2) można zapisać także jako:

(3)

Taka postać jest nawet łatwa do zapamiętania, bo jest to suma funkcji liniowej (A+Bx) oraz funkcji cosinus i sinus ((C1cos + C2sin)x).
Kod w Gretlu na nls (NMNK) dla modelu (3) - nie uwzględniając jeszcze parametrów wstępnych - byłby następujący:
 
...................................
l_Zamkniecie = A+B*(tc-time)^a+C1*(tc-time)^a*cos(w*ln(tc-time))+C2*(tc-time)^a*sin(w*ln(tc-time))

deriv A = 1
deriv B = (tc - time)^a
deriv C1 = cos(w*ln(tc - time))*(tc - time)^a
deriv C2 = sin(w*ln(tc - time))*(tc - time)^a

deriv a = B*ln(tc - time)*(tc - time)^a + C1*ln(tc - time)*cos(w*ln(tc - time))*(tc - time)^a + C2*ln(tc - time)*sin(w*ln(tc - time))*(tc - time)^a

deriv w = C2*ln(tc - time)*cos(w*ln(tc - time))*(tc - time)^a - C1*ln(tc - time)*sin(w*ln(tc - time))*(tc - time)^a

deriv tc = B*a*(tc - time)^(a - 1) + C1*a*cos(w*ln(tc - time))*(tc - time)^(a - 1) + C2*a*sin(w*ln(tc - time))*(tc - time)^(a - 1) + (C2*w*cos(w*ln(tc - time))*(tc - time)^a)/(tc - time) - (C1*w*sin(w*ln(tc - time))*(tc - time)^a)/(tc - time)
..................................


Jednak ciągle pozostaje pytanie jakie przyjąć wstępne parametry. Poprzednio zawsze przyjmowałem A = 1, B = -1, C = 0.5, a = 0.5, a także często w = 9.06, d = -1, tc zaczynałem od tc = T+1, gdzie T jest to liczba obserwacji. Trzeba znaleźć dodatkowo C1 i C2. Zgodnie ze wzorem podanym w [1] wiemy, że zachodzi:

Natomiast dotychczas stosowałem wstępne C = 0,5, a d = -1. Wobec tego wstępne C1 i C2 może wynieść odpowiednio 0,5 oraz -0.0087.

W przytoczonej publikacji [1] pokazany jest także dość skomplikowany algorytm na utworzenie wstępnych optymalnych parametrów liniowych. Należy rozwiązać następujące równanie macierzowe:

Aby nie powielać grafiki, wkleiłem bezpośredni obraz z tej publikacji. Zmienna m to nasza zmienna a, zmienna t(i) to t, indeks i to u nas też t, N to T. Wstępne liniowe parametry A, B, C1 i C2 są de facto funkcją pozostałych nieliniowych parametrów.


Literatura:
[1] Sornette, D., Filimonov, V. - A Stable and Robust Calibration Scheme of the Log-Periodic Power Law Model, 2013.

Czy model logperiodyczny może służyć do wyceny ryzykowanych akcji?

Dla wielu spółek już samo dopasowanie kursu do modelu log-periodycznego jest trudne albo niemożliwe. Ostatnio przyszedł mi do głowy taki pomysł. Jeżeli teoria Sornette'a-Johansena [1, 2, 3] jest prawdziwa, to są okresy, w których na giełdzie jest więcej spekulantów niż inwestorów (fundamentalnych). Dla jakich spółek takie okresy mogą występować najczęściej? Dość logiczne, że dla takich, które są wysoko spekulacyjne, tj. ich zyski są trudne do przewidzenia. Weźmy np. rynek gier komputerowych. Spółka latami pracuje nad jakimś projektem i w ciągu tego okresu ponosi tylko straty lub niewielkie zyski. Bardzo często przesuwana jest premiera samej gry i w zasadzie można od początku wziąć półroczną poprawkę na wstępną datę, bo ludzie (nawet specjaliści) najczęściej nie doszacowują potrzebnego czasu na zakończenie takiego dzieła. Kiedy już gra ujrzy światło dzienne, nie wiadomo czy odniesie sukces, a jeśli wiadomo, to nie jest pewne ile zarobi. Ale jeżeli odniesie sukces, to zysk może być tak duży, że podwoi czy potroi cały kapitał własny. W takiej sytuacji nie ma innej możliwości - kurs musi mocno pójść w górę. Jeżeli jednak spółka odniesie sukces, to dopiero zaczyna się kłopot. Inwestycje zwyczajnej spółki przyniosłyby nowy poziom cyklicznych przychodów, ale tutaj zysk z inwestycji jest jednorazowy. Z tego powodu wielu inwestorów unika takich spółek jak ognia: punktem zaczepienia dla nich zawsze jest kapitał własny, a w tym przypadku punkt taki nie istnieje. Jest to spowodowane wysoką niepewnością (wariancją) zysków monopolistycznych. W artykule Kiedy większa niepewność zwiększa wartość akcji? wyjaśniłem, że dla spółek o wysokim ROE w stosunku do kosztu kapitału własnego, P/BV naturalnie będzie wyższy: ta różnica zawiera zarówno średnią stopę zmian zysków monopolistycznych jak i jej wariancję, pomijając już inne momenty centralne.

Jeżeli akcje są tak wysoko spekulacyjne, to fundamentaliści ich nie tykają, czyli wycena również być może powinna opierać się na racjonalnym modelu spekulacyjnym. Zamiast klasycznie wyceniać, powinniśmy stworzyć model log-periodyczny. Natomiast dla spółek bezpiecznych, takich właśnie jak mBank, który cyklicznie płaci dywidendy, a jego zyski są w miarę do przewidzenia i beta nie jest zbyt wysoka, model ten słabo się sprawdza, co pokazałem w poprzednim artykule. Dlatego tym razem sprawdzę NMNK w Gretlu 3 spółki: CD Projekt (CDR), CI GAMES (CIG) i 11Bit (11B).


1. CDR (T = 2021). Okres 2009-2017 do 26.01.2017. Użyłem kodu:
.......................
scalar A = 1
scalar B = -1
scalar C = 0.5
scalar a = 0.5
scalar w = 15
scalar d = -1
scalar tc = 2100

l_Zamkniecie = A+B*(tc-time)^a*(1+C*cos(w*ln(tc-time)+d))
deriv A = 1
deriv B = (tc-time)^a*(1+C*cos(w*ln(tc-time)+d))
deriv C = B*(tc-time)^a*cos(w*ln(tc-time)+d)
deriv a = (tc-time)^a*(B+B*C*cos(w*ln(tc-time)+d))*ln(tc-time)
deriv w = -B*C*(tc-time)^a*sin(w*ln(tc-time)+d)*ln(tc-time)
deriv d = -B*C*(tc-time)^a*sin(w*ln(tc-time)+d)
deriv tc = -B*C*w*(tc-time)^(a-1)*sin(w*ln(tc-time)+d)+B*a*(tc-time)^(a-1)*(1+C*cos(w*ln(tc-time)+d))
.......................

gdzie l_Zamkniecie to logarytm z kursu zamknięcia, a wszystkie parametry są takie jak opisałem poprzednio.

 Dostajemy regresję w postaci niebieskiej linii:

Chociaż model nie wskazuje, aby w najbliższym czasie doszło do krachu (tc > 2700), to akcje wydają się przewartościowane, znajdując się powyżej krzywej regresji. Zauważmy, że obecnie C/WK = 8,23. Aby wycena była zgodna z modelem C/WK musi wynieść 5,56.


2a. CIG (T = 1770). Okres 2010-01-04 - 2017-01-27. To trudniejszy przypadek, bo nie mogłem znaleźć odpowiednich wstępnych parametrów. Pytanie brzmi czy moglibyśmy się dowiedzieć, w jakim oknie czasu użyć modelu. Aby na to odpowiedzieć, można użyć tc < T, a więc znaleźć osobliwość w przeszłości. To też nie jest prosta sprawa. Nie mogłem użyć parametru w w typowym zakresie 5-20. Użyłem więc kodu:
.................
scalar A = 1
scalar B = -1
scalar C = 0.5
scalar a = 0.5
scalar w = 35
scalar d = -1
scalar tc = 1780

l_Zamkniecie = A+B*(tc-time)^a*(1+C*cos(w*ln(tc-time)+d))
deriv A = 1
deriv B = (tc-time)^a*(1+C*cos(w*ln(tc-time)+d))
deriv C = B*(tc-time)^a*cos(w*ln(tc-time)+d)
deriv a = (tc-time)^a*(B+B*C*cos(w*ln(tc-time)+d))*ln(tc-time)
deriv w = -B*C*(tc-time)^a*sin(w*ln(tc-time)+d)*ln(tc-time)
deriv d = -B*C*(tc-time)^a*sin(w*ln(tc-time)+d)
deriv tc = -B*C*w*(tc-time)^(a-1)*sin(w*ln(tc-time)+d)+B*a*(tc-time)^(a-1)*(1+C*cos(w*ln(tc-time)+d))
....................

Dostajemy następujący wykres:

Wcale to nie znaczy, że wyznaczony punkt osobliwości jest wielkością absolutną. Np. gdy ustawiłem tc = 1695, otrzymałem:

Jednak tylko dla dość wąskiego zakresu mogłem dostać jakieś wartości, więc można przyjąć, że jest to obszar rozpoczęcia nowego trendu. Dlatego przyjmę nowe okno czasu:

2b. CIG (T = 624). Okres: 2014-08-01 - 2017-01-27. Mimo przyjęcia nowego zakresu, wyznaczenie wstępnych parametrów nadal sprawia trudności. W końcu przyjąłem:

scalar A = 1
scalar B = -1
scalar C = 0.5
scalar a = 0.5
scalar w = 20
scalar d = -1
scalar tc = 2500

Wyniki:

Tym razem CIG wydaje się prawidłowo wyceniony z punktu widzenia modelu spekulacyjnego. Jest tak mimo wysokiego C/WK = 6,36.


3. 11B (T = 1554). Okres 2010-10-28:2017-01-26. Jest to dobry przykład ruchu Levy'ego, dla którego wariancja jest nieskończona. Tym razem ustalenie wstępnych parametrów było bardzo łatwe, bo wystarczyło przyjąć standardowe (np. tc = T+1):

.....................
scalar A = 1
scalar B = -1
scalar C = 0.5
scalar a = 0.5
scalar w = 9.06
scalar d = -1
scalar tc = 1555
......................

Reszta bez zmian.

Wyniki:

Sytuacja jest ciekawa z dwóch powodów. Po pierwsze Spółka zgodnie z tym modelem jest niedowartościowana mimo wysokiego C/WK = 8,45. Model wskazywałby na wzrost C/WK do 12,95. Po drugie prognozowany tc = 1602,58, a więc zostało niecałe 50 dni do szacowanego załamania. Oczywiście ostatnie testy na WIG (dla początku bessy 2007) dobrze ilustrują jak istotna jest aktualizacja modelingu. Tamte testy sugerują, że trzeba myśleć o wyjściu z rynku jeśli tp = tc - Z, gdzie tp to data prognozowania, tj. tworzenia prognozy, a Z to liczba dni, która waha się między 5 a 7.
To czy hipoteza "spekulacyjnej wyceny" się sprawdzi, przekonamy się w najbliższych tygodniach.


Literatura:

[1] Sornette, D., Johansen, A. - Critical Market Crashes, 1999,
[2] Sornette, D., Johansen A., Ledoit, O. - Predicting Financial Crashes Using Discrete Scale Invariance, Feb 2008,
[3] Sornette, D., Johansen A. - Significane of log-periodic precursors to financial crashes, Feb. 1, 2008.

Zmagania z modelem log-periodycznym

Do teorii log-periodycznej od dawna byłem sceptycznie nastawiony, a swoją krytykę wyraziłem kiedyś w tym artykule. Z drugiej strony jestem zwolennikiem teorii chaosu (choć może nie deterministycznego), a więc także nieokresowych i nietrywialnych cykli. Ekonofizyka dostarcza także uzasadnienie powstania tzw. log-periodyczności. Nie jest wykluczone, że dla niektórych okresów lub niektórych walorów, teoria ta może się sprawdzić i tym samym wspomóc inwestora czy spekulanta w podjęciu trudnych decyzji. Co więcej, Sornette i Johansen [1] rozważają najpierw w swoim modelu "ograniczoną racjonalność" traderów (która wynika nie tylko z ułomności ludzkiego umysłu, ale także z natłoku informacji), a następnie [2, 3, 4] tworzą model w ramach racjonalnych oczekiwań, zgodnie z którym moment krachu można prognozować, ale tylko z pewnym prawdopodobieństwem. Ogólnie autorzy twierdzą, że gracze sami "się nakręcają" i kreują dodatnią warunkową oczekiwaną stopę zwrotu, która staje się tym wyższa im bliżej jest krachu. Ale staje się ona wyższa nie dlatego, że gracze "nakręcają się" w sposób nieracjonalny, ale dlatego, że gracze wymagają od rynku wyższej oczekiwanej stopy zwrotu właśnie za to, że się nakręcają. A nakręcają się w sposób racjonalny, dlatego że zdają sobie sprawę, że - w przypadku trendu rosnącego - kupując w takiej fazie, więcej ryzykują. Im bliżej krachu, tym więcej ryzykują, a więc wymagają większego zwrotu. Rozdzielając oczekiwaną stopę zwrotu na prawdopodobieństwo i wielkość ruchu, można powiedzieć, że prawdopodobieństwo dalszego (czyli warunkowego) wzrostu spada, natomiast zakres ruchu rośnie. Natomiast niewarunkowa stopa zwrotu pozostaje równa zero. Aby dobrze zrozumieć różnicę między warunkową a niewarunkową stopą zwrotu, dobrze najpierw przeczytać wpis Smarujący estymator.

Autorzy podkreślają, że nie wystarczy tylko raz zastosować model, który wyprognozuje moment krytyczny i czekać do tego okresu. Jeżeli model wskazuje moment krytyczny za rok, to w ciągu tego roku może się struktura zmienić, więc należy aktualizować model. To jest dodatkowy stochastyczny element ich teorii.

Jest wiele różnych wersji modelu log-periodycznego, ale właściwie wszędzie pojawia się wzór, który w uproszczeniu wyprowadzę idąc tokiem rozumowania Kutnera [5]. Ogólnie biorąc musimy połączyć dwie koncepcje: jedną ze statystyki - rozkład Levy'ego-Pareto i jedną z fizyki - temperatury krytycznej. Podzielę to na dwie części.

1) Rozkład Pareto-Levy'ego jest związany z grubymi ogonami, które dobrze są nam znane, więc nie będę się o nim rozpisywał. Jeśli cenę akcji P(t) da się opisać rozkładem proporcjonalnym do:

(1)

to mamy do czynienia z rozkładem Pareto dla t > 0. Zwróćmy uwagę, że z jednej strony wzór (1) opisuje prawdopodobieństwo (zmiany) ceny, ale z drugiej wartość oczekiwana będzie proporcjonalna do tego prawdopodobieństwa. Zgodnie ze wzorem (1) dla każdego okresu t mamy inne prawdopodobieństwo. Gdybyśmy przemnożyli obie strony przez cenę P(t), to dostalibyśmy wartość oczekiwaną ceny dla okresu t. Stąd w miejsce prawdopodobieństwa możemy wstawić po prostu oczekiwaną cenę.

Znaną własnością rozkładu Pareta jest równanie skalowania:

(2)

gdzie L^a to czynnik skalujący funkcję P(t).

Najogólniejszym rozwiązaniem osobliwym (tzn. rozwiązaniem, które nie posiada zapisu zgodnego z całką ogólną - gdyż mamy tu do czynienia z równaniem różniczkowym zwyczajnym) równania skalowania (2) jest

(3)

Funkcję F(u) można rozwinąć w szereg Fouriera:

(4)

2) W złożonych systemach istnieją różne fazy, w których pewne parametry fizyczne / ekonomiczne pozostają względnie stałe. W fizyce takimi parametrami są temperatura lub ciśnienie. Np. faza topnienia następuje w temperaturze poniżej 0 stopni Celsjusza, faza zamarzania - od 0 stopni wzwyż, a faza wrzenia - 100 stopni. Hołyst, Poniewierski i Ciach definiują fazę jako "makroskopowo jednorodny stan układu, odpowiadający danym parametrom termodynamicznym." [6]. Dalej: "Proces przekształcania się jednej fazy w inną nazywa się przejściem fazowym lub przemianą fazową". Różne fazy mogą ze sobą współistnieć (stąd często w przejściach między jesienią a zimą oraz zimą i wiosną utrzymuje się temperatura 0 stopni), ale w przypadku ciągłych przejść fazowych, jedna faza przechodzi bezpośrednią w inną. "Ciągłe przejścia fazowe mają na ogół charakter przemiany typu porządek-nieporządek. Przemianą tego typu jest np. przejście paramagnetyk-ferromagnetyk, występujące w materiałach magnetycznych, takich jak żelazo. Uporządkowanie dotyczy tutaj mikroskopowych momentów magnetycznych umiejscowionych w węzłach sieci krystalicznej. W fazie paramagnetycznej orientacje momentów magnetycznych są chaotyczne, więc jeśli nie ma zewnętrznego pola magnetycznego, to magnetyzacja układu znika. Jest tak wówczas, gdy temperatura układu jest wyższa od pewnej charakterystycznej temperatury Tc, zwanej temperaturą Curie. Natomiast w temperaturze niższej od Tc, mikroskopowe momenty magnetyczne porządkują się spontanicznie wzdłuż pewnego wspólnego kierunku, i magnetyzacja przyjmuje wartość różną od zera. Istotne jest to, że magnetyzacja pojawia się spontanicznie, bez udziału zewnętrznego pola magnetycznego, jako efekt oddziaływania pomiędzy mikroskopowymi momentami magnetycznymi." Tak więc temperatura Curie to temperatura krytyczna dla przemian magnetycznych, która charakteryzuje jednocześnie obszar krytyczny.

Kutner pisze, że w obszarze krytycznym większość wielkości fizycznych zmienia się w zależności od temperatury T według prawa potęgowego:

(5)

gdzie Tc to temperatura krytyczna.

Aby zastosować pojęcie temperatury krytycznej do rynku, zastąpimy temperaturę T czasem t. Jest to chyba najważniejszy moment w zrozumieniu zastosowania fizyki do giełdy: temperaturę określamy jako wielkość proporcjonalną do czasu.

Punkt 1, który jest czysto matematyczny, wydaje się zupełnie logiczny, ale zawiera założenie, że szukamy tylko rozwiązania osobliwego (a nie ogólnego). To założenie jest potrzebne, aby spełniona została interpretacja fizyczna z pktu 2, mianowicie istnienia temperatury krytycznej, a więc dla ekonofizyki - czasu krytycznego. Natomiast czas krytyczny jest potrzebny po to, aby spełniona została koncepcja "racjonalnej (lub ograniczenie racjonalnej) bańki spekulacyjnej".

Technicznie rzecz biorąc zmienna (t - tc) stanie się ujemna, bo wielkość tc z założenia ma być większa od każdego t w którym operujemy: model ma prognozować przyszłość, a nie przeszłość. Dlatego od razu użyjemy zmiennej -(t-tc) = (tc - t). Następnie, nie interesuje nas za bardzo wykres z argumentami tc-t, bo przecież chcemy widzieć normalny przebieg czasu na wykresie. Punkt krytyczny tc jest parametrem do oszacowania, a więc stałą. Dlatego stworzymy zmienną P(t) zamiast P(tc - t). Stąd za P(tc - t)  podstawimy P(t). Jeżeli uprościmy szereg Fouriera w (4) do pierwszego rzędu, dostaniemy w końcu model log-periodyczny:

(6)

gdzie A, B, C, d to pewne stałe oraz

(7)

Do oszacowania parametrów zastosuję NMNK w Gretlu, której praktyczne zastosowanie szczegółowo opisałem w poprzednim artykule
Nieliniowa metoda najmniejszych kwadratów dla modelu trendu. Algorytm Levenberga–Marquardt może w końcu przydać się do czegoś praktycznego, bo poprzednie modelowanie trendu nieliniowego za pomocą funkcji wykładniczej, jak pokazałem, nie ma większego sensu. W przypadku skomplikowanych nieliniowych trendów z cyklami i krachami sprawa wygląda zupełnie inaczej. Tak więc algorytm jest analogiczny do tamtej funkcji. Algorytm Levenberga–Marquardt został także użyty przez Sornette'a i Sammisa [7], którzy jako jedni z pierwszych używali modelu (6) - ich pierwsze próby dotyczyły przewidywania trzęsień ziemi.

Kiedy zacząłem testować (6) szybko okazało się, że wiele zależy od ustawienia początkowych parametrów: a, d , w i tc. Algorytm wprawdzie sam je szacuje, ale potrzebuje danych wejściowych. W wielu sytuacjach model nie zbiega do wybranej funkcji. Stąd warto posłużyć się wynikami uzyskanymi przez innych badaczy. Drożdż, Grummer, Ruf i Speth [8] empirycznie dowodzą, że dla większości znaczących, historycznych finansowych zdarzeń, preferowana wartość parametru L = 2. Na podstawie wzoru (7) dostaniemy więc, że preferowane w równa się ok. 9,06. Następnie, w [9] autorzy stwierdzają, że jeśli 0 < a < 1, to cena w skończonym czasie dojdzie do tc. I jeszcze na koniec znalazłem jedną z najnowszych publikacji Sornette'a i Filimonova [10], którzy po zebraniu wielu danych, skompilowali parametry do następujących ograniczeń:
0.1 ≤ a ≤ 0.9,
6 ≤ w ≤ 13,
|C| < 1
B < 0.

Jeśli chodzi o ostatnią nierówność, to jest prawdopodobne, że B > 0 dla trendu spadkowego - znalazłem w [11]. Piszę prawdopodobnie, bo autor popełnił tam błąd we wzorze na w, więc nie mam pewności czy gdzieś indziej nie ma błędu.

Jeśli chodzi o początkowe tc, to jak sądzę preferowane będzie T+e gdzie T to liczba obserwacji, a e to liczba dni, po której spodziewalibyśmy się załamania (lub ewentualnie zmiany bessy na hossę) od momentu T.

Modele log-periodyczne w trzech ostatnich wspomnianych pracach opierają się na logarytmach ceny, czyli mają postać:

(8)

Tego właśnie modelu użyję.


Przykład 1. WIG: notowania dzienne 1994-13.01.2017 (T = 5704 obserwacji). Przy preferowanych parametrach modelu nie mogłem otrzymać. Dopiero po wpisaniu następujących wstępnych parametrów:
A = 1, B = -1, C = 0.5, a = 0.5, w = 15, d = -1, tc = 5800 uzyskałem model:

 Oszacowane tc = 7405,03 (p-value 1%). Z tego punktu widzenia krach nam nie straszny: 7405 - 5704 = 1701 dni pozostało do ewentualnego krachu. Jest to oczywiście tak odległa perspektywa, że nie ma sensu brać tego na poważnie. 

Zamiast tego cofnijmy się do końca czerwca 2007. Liczba danych = 3316. Ustawione preferowane początkowe parametry wystarczyły: A = 1, B = -1, C = 0.5, a = 0.5, w = 9.06, d = -1, tc = 3317. Tym razem model robi wrażenie:

Otóż oszacowane tc wyniosło 3321,68 (p-wartość 1%). Natomiast faktyczna bessa zaczęła od 3322 dnia (7.07.2007). Trafiło w punkt. W momentu prognozy do oszacowanego dnia załamania pozostało 5-6 dni (3321,68 - 3316).
Wydawałoby się, że potrafimy przewidywać przyszłość. Nie do końca. Gdy ustawimy dane do końca maja (3296 danych), to dostaniemy tc = 3301,19, czyli o 20 dni za wcześnie, ale 5 dni od dnia, w którym dokonalibyśmy prognozy (3301-3296=5). To samo, gdy ustawimy datę końcową koniec kwietnia (3275): dostaniemy tc = 3282,11. Tym razem jednak czas do prognozowanego krachu jest nieco większy (3282-3275=7 dni). Weźmy jeszcze koniec grudnia 2006 (3192 danych). Dostałem tc = 3213,42. Czas do szacowanego krachu jest znacznie większy (3213-3192=21 dni).

Zwracam uwagę, że nie ma znaczenia jaką ustawimy datę początkową tc, zawsze wyjdzie to samo. Odpowiednia wstępna wielkość tc jest potrzebna tylko po to, by algorytm "załapał" ten parametr. W powyższych przykładach najczęściej wpisywałem tc = T+1.

Tak więc decydującym jest ciągła aktualizacja modelu (8), tak jak wcześniej podkreślali to Sornette i Johansen. A mimo to możemy uzyskiwać fałszywe sygnały, o czym przekonamy się, generując prognozę w dniu poprzedzającym początek bessy, czyli 6.07.2007: znów przesunęłaby się prognoza krachu o ok. 5-6 dni (T = 3321 oraz tc wyniósłby 3326,6, czyli 3326,6-3321=5,6). Ta sytuacja będzie codziennie się powtarzać, przez cały lipiec, a nawet w kolejnych miesiącach.

Przykład 2. Mbank: roczne 1994-2015 (T = 22 obserwacje). Wróćmy jeszcze raz do mbanku, który ostatnio modelowałem regresją nieliniową, tyle że zwykłą funkcją wykładniczą. Tym razem możemy znaleźć o wiele dokładniejsze przewidywania przy tych samych danych. Aby dostać model użyłem: A = 1, B = -1, C = 0.5, a = 0.5, w = 16, d = -1, tc =23. NMNK oszacował tc = 24,87, a wykres jest taki:

Jednakże obecnie możemy już dodać rok 2016. Pytanie czy wielkość tc zmieni się? Użyłem tych samych wstępnych parametrów. NMNK oszacował ponownie tc = 24,87, a wykres jest taki:

 Czyli wg modelu mamy spodziewać się załamania za 1-2 lata.

Aby jednak nie napawać się zbytnio optymizmem, pokażę teraz, że model (8) kiepsko radził sobie z dziennymi wahaniami.


Przykład 3. Mbank: dzienne 1994-koniec 2013 (T = 4941 obserwacji): Wpisałem następujące wstępne parametry:
A = 1, B = -1, C = 0.5, a = 0.5, w = 9.06, d = -1, tc = 5000. Uzyskałem model o wykresie:

Ogólnie model na rysunku wydaje się całkiem dobry. Parametr krytyczny tc został oszacowany na 5507,77 i jest istotny statystycznie na poziomie 1% (tak samo jak reszta parametrów). czyli krachu powinniśmy oczekiwać po 5507,77-4941 = 566,77 dniach. Dodatkowo: Błąd standardowy reszt  = 0,252757, Skorygowany R-kwadrat   0,890034. Co więc się stało po tym czasie? Poniżej zamieściłem ten sam wykres powiększony o 567 dni.

A do dziś mamy:

Już dawno po "krachu". Model powinien przewidywać go w momencie gdy tworzyliśmy prognozę, bo od tego momentu trend się zmienił. Ale można byłoby starać się obronić model, bo kurs od momentu wykonania prognozy, czyli końca 2013, przez kolejne pół roku stał w miejscu, więc należałoby aktualizować model i być może wtedy uzyskalibyśmy moment wyjścia? Nic z tego. Przesuwając dane do końca lipca 2014 (5087) dostaniemy tc = 5588,87 i wykres:

Zatem czekalibyśmy, bo przecież różnica 5589-5087 = 502, czyli jeszcze ok. 2 lata dni roboczych.

Powyższe bardzo skrótowe testy pokazały, że model log-periodyczny może rzeczywiście służyć jako wskaźnik "temperatury rynku" czy zwiększonej niepewności dla racjonalnego inwestora, tak że spekulacja zaczyna przeważać nad wyceną fundamentalną. Ale kontrowersyjne jest twierdzenie, że pozwala przewidywać zmianę trendu. Możliwe, że rynek zachowuje się tak jak to opisuje teoria Sornette-Johansena [2, 3, 4]. Fakt pozostaje faktem, że analiza WIG wykazała, że im bliżej był dzień zmiany trendu w 2007, tym model (8) wskazywał na coraz bliższą datę od momentu prognozy, przy czym krańcowym czasem pozostałym do załamania był mniej więcej 1 tydzień.

Na sam koniec stworzę prognozę dla indeksu USA dla częstości rocznej i miesięcznej.

Przykład 4. S&P500 roczne: 1933-2016 (T=84 dane). Wstawiłem standardowe parametry, w tym tc = 85. W odpowiedzi otrzymałem tc = 94,355. Czyli do krachu stulecia jeszcze 10 lat.

Najgorsze rezultaty model osiągnął w drugiej połowie lat 90 XX w. Można to nawet potraktować jako argument za przewartościowaniem akcji w tym okresie.

Przykład 5. S&P500: miesięczne 1933-koniec 2016 (T=1008). Ustawienia: identyczne co poprzednio, ale nie chciało wejść z tc = 1009 i dopiero dla tc = 1020 "załapało". Prognoza tc = 1126,55, a wykres przedstawia się:

W powiększeniu ostatnich okresów widać, że model wchodzi w fazę wzrostu:

Jeżeli prognoza się sprawdzi, to czeka nas krach w USA za 119 miesięcy, czyli za 119/12 = 9,9 lat. Prognoza miesięczna idealnie więc pokrywa się z prognozą roczną.


Literatura:
[1] Sornette, D., Johansen, A. - Modeling the stock market prior to large crashes, 1999,
[2] Sornette, D., Johansen, A. - Critical Market Crashes, 1999,
[3] Sornette, D., Johansen A., Ledoit, O. - Predicting Financial Crashes Using Discrete Scale Invariance, Feb 2008,
[4] Sornette, D., Johansen A. - Significane of log-periodic precursors to financial crashes, Feb. 1, 2008,
[5] Kutner, R., Wprowadzenie Do Ekonofizyki: Niegaussowskie Procesy Stochastyczne Oraz Niedebye'Owska Relaksacja W Realu. Elementy teorii ryzyka rynkowego wraz z elementami teorii zdarzeń ekstremalnych, W-wa czerwiec 2015,
[6] Hołyst, R., Poniewierski A., Ciach A., Termodynamika Dla Chemików, Fizyków I Inżynierów, Październik 2003,
[7] Sornette, D., Sammis, C., - Complex critical exponents from renormalization group theory of earthquakes Implications for earthquake predictions, 1995,
[8] Drożdż S., Grummer, F., Ruf, F., Speth, F. - Log-periodic self-similarity an emerging financial law, 2002,
[9] Fantazzini, D. ,Geraskin, P., - Everything You Always Wanted to Know about Log Periodic Power Laws for Bubble Modelling but Were Afraid to Ask, Feb 2011,
[10] Sornette, D., Filimonov, V. - A Stable and Robust Calibration Scheme of the Log-Periodic Power Law Model, 2013,
[11] Górski, M. - Zastosowanie Teorii Log-Periodyczności W Prognozowaniu Krachów Giełdowych, 1/2014.