(1)
oraz wiedząc, że parametr b jest nieznany, tak że możemy jedynie
oszacować jego wartość na podstawie próby losowej, to wartość
oczekiwana stopy zwrotu (R) może być oszacowana za
pomocą modelu:
(2)
gdzie b z falką to estymator MNK z modelu ln(P) = b*T + składnik losowy.
Wyraz k wyraża błąd retransformacji z postaci liniowej do nieliniowej (pierwotna jest postać nieliniowa, która jest transformowana do liniowej przez logarytmowanie, aby zastosować MNK; następnie powracamy do postaci nieliniowej, czyli dokonujemy retransformacji). Jak widać przy nieco większym T, wyraz k ma bardzo mały wpływ.
Geometryczny ruch Browna zakłada jednak rozkład log-normalny. Z tym rozkładem jest ten problem, że jego lewy ogon bardzo szybko
zbiega do zera:
W
rzeczywistości dobrze wiemy, że na giełdach zdarzają się rzadkie, ale
bardzo silne odchylenia, a także asymetria. Kwartalny sWIG80 od 01.1994 do 03.2016 (87 obserwacji) miał
minimum na poziomie -40%, a maksimum prawie +54%. Poniżej jest wykres
oszacowanego rozkładu sWIG80 (zrobiony w Gretlu za pomocą jądra Gaussa -
metoda ta daje zniekształcony obraz, bo sugeruje, że wystąpiły wartości
poniżej -40%, co jest nieprawdą):
W tym wypadku lepszy okazuje się rozkład normalny, choć występuje tu pewna prawostronna skośność.
Duan
[1] przedstawił metodę retransformacji, która nie zakłada z góry żadnego rozkładu.
Duan nazwał swój estymator "smarującym estymatorem" (smearing
estimate). Pokazał, że jego estymator daje lepsze rezultaty, tzn. jest
bardziej efektywny, gdy rozkład stopy zwrotu nie jest log-normalny, a
więc gdy logarytmiczna stopa zwrotu nie posiada rozkładu Gaussa.
Smarujący estymator (SE) dla oczekiwanej stopy zwrotu można zapisać następująco:
(3)
Wariancja składnika losowego jest tym razem stała w czasie, czyli występuje jednocześnie homoskedastyczność i stacjonarność składnika losowego. Składnik losowy jest tutaj różnicą pomiędzy sąsiadującymi składnikami losowymi modelu logarytmicznej ceny, dlatego że pierwotny składnik losowy w modelu (1) jest niestacjonarny (porównaj zapis wariancji w obu przypadkach). Oczekiwana stopa zwrotu powstała po prostu przez zapis:
Nic więc dziwnego, że aproksymacją będzie:
(4)
Korekta
Duana to zwykła średnia arytmetyczna kolejnych stosunków reszt z regresji liniowej.
Gdy rozkład log-stopy jest normalny i znamy pełną populację to (4) sprowadza się do:
oraz gdy jest normalny i nie znamy pełnej populacji, to z modelu (2) wynika, że:
Model (3) można więc traktować jako uogólnienie (2). Trzeba jednak zaznaczyć, że oryginalny wzór Duana jest nieco bardziej ogólny niż ten, który podałem w (3): w naszym przypadku rolę zmiennej objaśniającej pełni zmienna czasowa, która się redukuje, natomiast w oryginale jest zastąpiona zmienną x, która może być dowolna (wtedy też w modelu (3) ocena parametru b z falką będzie przemnożona dodatkowo przez x).
Model (3) pozwala też zrozumieć zależności pomiędzy średnią warunkową a niewarunkową.
Jeżeli nie istnieje liniowa korelacja między okresem T a logarytmiczną ceną
ln(P), czyli gdy ocena b = 0 w modelu (1), to oczekiwana stopa zwrotu w (3) sprowadza się
do zwykłej średniej arytmetycznej:
Przykład.
Aby
porównać model (2) z (3), użyję tych samych danych co poprzednim razem,
tj. dla mbanku - rocznie 1994-2015 (22 obserwacje). Nie będę się
wgłębiał w to czy stopy mbanku są normalne, lognormalne czy jeszcze inne. Zaczynamy od zlogarytmowanego modelu (1):
Parametr b wyniósł 11,18%. Korzystając z Gretla uzyskałem reszty powyższej regresji liniowej, które podstawiłem do wzoru (4), czyli korekty SE. Korekta ta wyniosła 1,0699. Podstawmy to do (3):
Dla porównania stosując
model (2) uzyskałem wielkość 18.69%, natomiast dla standardowego wzoru
na wartość oczekiwaną w rozkładzie lognormalnym (czyli dla k = 0)
18.73%. Dodatkowo przypomnę, że średnia arytmetyczna wyniosła 20,08%, a
geometryczna 11,71%. Pamiętać trzeba, że geometryczna średnia dotyczy
tylko inwestycji długoterminowej, dlatego SE staje się konkurencyjny głównie w
stosunku do średniej arytmetycznej (która będzie poprawna w sytuacji, gdy logarytmiczna cena nie jest liniowo skorelowana z okresem czasu) oraz do estymatora z (2) (który jest poprawny dla próby w rozkładzie log-normalnym).
Literatura:
[1] N. Duan, Smearing Estimate: A Nonparametric Retransformation Method, Sep. 1983








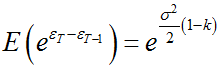


Brak komentarzy:
Prześlij komentarz