Minimalny udział aktywów ryzykownych w portfelu to 15-30%?

Przyszedł mi do głowy pomysł, który może ułatwić inwestorom przyjąć optymalny udział akcji lub innych aktywów ryzykownych w portfelu. Wiadomo, że nie istnieje taki poziom w sensie absolutnym, bo zależy od awersji do ryzyka konkretnego inwestora. Jeżeli jednak przyjmiemy założenie, że oczekiwany zysk powinien się równać co najmniej potencjalnej stracie, to dostaniemy już bardzo konkretny udział zależny od 3 parametrów: stopy wolnej od ryzyka (Rf), oczekiwanej stopy zwrotu z portfela rynkowego (Rm) albo naszego własnego portfela akcji (Rw), odchylenia standardowego (D) albo średniej straty (SDs). 

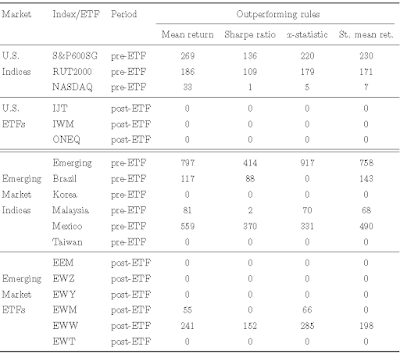
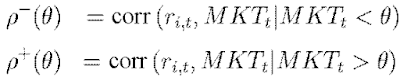Klasyczna formuła na semi-wariancję z próby to

gdzie
r(t) - stopa zwrotu
R - oczekiwana stopa zwrotu (średnia)
T - liczba obserwacji.

Mechanizm jest prosty: jeśli różnica między stopą zwrotu a średnią jest dodatnia, wtedy odrzucamy ją i zastępujemy zerem. Jeśli jest ujemna, wtedy przyjmujemy ją i podnosimy do kwadratu.

Ze względu na występujące zera SV zawsze będzie mniejsza od wariancji. Gdy mamy do czynienia z rozkładem symetrycznym, wariancja będzie dwa razy większa od SV (dla której zera będą się symetrycznie rozkładać z nie-zerami). Żeby więc sprawdzić symetryczność rozkładu, można podwoić SV i sprawdzić czy jest bliska wariancji.

Jeżeli jednak chcemy stworzyć miarę ryzyka związaną z potencjalną stratą, to nie możemy użyć SV, bo r(t) < R nie oznacza jeszcze straty. Dlatego w miejsce R możemy wstawić zero:

Taka miara ryzyka jest już sensowna, ale ciągle ze względu na występujące zera będzie zaniżać całkowitą stratę - w końcu dzielimy sumę przez liczbę wszystkich obserwacji (a więc też z zerami). Dla dużej liczby danych zastosowałbym miarę uwzględniającą tylko straty:

Aby uzyskać średnią stratę, wyciągniemy pierwiastek kwadratowy:

Powiedzmy, że mamy kapitał początkowy K. Przewidujemy, że w kolejnych okresach może się zdarzyć średnia strata S. Stratę zapiszemy jako procentowe pseudo-semi-odchylenie standardowe, SDs, przemnożone przez K:

(1)

Wymagamy, aby w następnych okresach oczekiwany zysk wyniósł co najmniej S, aby wyrównać stratę. Ktoś powie, że nie możemy czegoś wymagać od rynku. Nie możemy sami, ale jako zbiorowość inwestorów już tak. Zakładamy, że wszyscy inwestorzy mają takie samo minimalne wymaganie. Będzie to oznaczało, że oczekiwana stopa zwrotu (równa stopie dyskontowej - to znaczy, że kapitał jest odpowiednio dyskontowany, tak aby w przyszłości mógł wzrosnąć - na tym polega idea wymaganej stopy zwrotu; jeśli ktoś ma tu wątpliwości, niech przeczyta mój komentarz do poprzedniego artykułu, gdzie szczegółowo wyjaśniłem ten problem) będzie równa:

(2)

Zgodnie z CAPM-CML stopa zwrotu z portfela to kombinacja liniowa stopy wolnej od ryzyka (systematycznego), Rf, i stopy zwrotu z portfela rynkowego, R(M):

(3)

gdzie x to udział instrumentu bez ryzyka, zaś 1-x to udział portfela rynkowego w całym portfelu.

Podstawiamy (2) do (3):

(4)

Rozwiązujemy (4) względem x:

(5)

Klasyczna postać CAPM-CML to:

(6)

gdzie:
D - odchylenie standardowe portfela inwestora
D(M) - odchylenie standardowe portfela rynkowego

Aby dopasować CML do naszego modelu, w miejsce D i D(M) w (6) wstawimy SDs i SD(M)s:

(7)

Za Rp wstawiamy uzyskany wynik w (2):

(8)

Rozwiązujemy to równanie względem SDs. Dostaniemy 2 rozwiązania, wśród których jedno jest ujemne - odrzucamy je. Pozytywne rozwiązanie podstawiamy do równania (5) na x. Ze względu na dwa rozwiązania SDs ogólnie dostaniemy też dwa rozwiązania względem x:

x1 =  -(Rf - Rm + SD(M) - Rf*SD(M) + 2*Rm*SD(M) - (Rf^2*SD(M)^2 - 2*Rf^2*SD(M) + Rf^2 + 2*Rf*Rm*SD(M) - 2*Rf*Rm + 2*Rf*SD(M)^2 + 2*Rf*SD(M) + Rm^2 - 2*Rm*SD(M) + SD(M)^2)^(1/2))/(2*SD(M)*(Rf - Rm))

x2 =  -(Rf - Rm + SD(M) - Rf*SD(M) + 2*Rm*SD(M) + (Rf^2*SD(M)^2 - 2*Rf^2*SD(M) + Rf^2 + 2*Rf*Rm*SD(M) - 2*Rf*Rm + 2*Rf*SD(M)^2 + 2*Rf*SD(M) + Rm^2 - 2*Rm*SD(M) + SD(M)^2)^(1/2))/(2*SD(M)*(Rf - Rm))

Poprawne rozwiązanie wynikać będzie z dodatniego rozwiązania SDs. Ale tak naprawdę nie trzeba tego podstawiać do x, wystarczy, że spośród tych dwu powyższych rozwiązań jedno będzie dodatnim ułamkiem (będzie jednocześnie posiadać dodatnie SD). Drugie odrzucamy.

Przykład 1.
S&P 500 w okresie 1941-2017 posiada średnią stopę zwrotu 8,7%, odchylenie standardowe D(M) = 16,3%, a SD(M)s = 16,1%. Chociaż D(M) jest praktycznie równe SD(M)s, to pamiętajmy, że nie oznacza to symetryczności rozkładu. Popatrzmy zresztą na histogram stóp zwrotu:

Mamy tu lewostronną skośność - oznacza to, że semi-wariancja lewostronna jest większa od semi-wariancji prawostronnej. Jednak straty nie są wcale większe od zysków - zauważmy, że dominanta wynosi 13,7% (częstość = 19). Czyli większa masa kumuluje się po stronie zysków. Istnieje wprawdzie gruby ogon na stratach, ok -38%, ale występuje więcej obserwacji powyżej 0.

Paradoksalnie więc możemy stosować zwykłe odchylenie standardowe, które okazuje się zbliżone do średniej straty. Czyli wiemy, co podstawić pod Rm i SD(M)s. Ale pytanie co podstawić pod Rf? Zwracam uwagę, że Rm = 8,7% to średnia arytmetyczna. Z poprzedniego artykułu wiemy, że trzeba w takiej sytuacji stosować krótkoterminowe stopy zwrotu, a więc także krótkoterminową rentowność obligacji skarbowych, a ściślej mówiąc 1-roczną. Na podstawie http://www.multpl.com/1-year-treasury-rate/ możemy uzyskać dokładne dane statystyczne. Obecnie 1-roczna stopa z obligacji skarbowych USA wynosi 2,24%. Jednakże operujemy średnimi i sztucznie byłoby zastosować bieżącą rentowność - mimo iż stosowane stopy do CAPM powinny określać przyszłość a nie przeszłość. W dodatku stopy rentowności okazują się niestacjonarne, co dodatkowo komplikuje analizę. Nie bądźmy jednak zbyt pedantyczni. Portal Shillera stwierdza, że średnia rentowność to 3,08%, więc przyjmijmy 2,5% oraz 3%. Dlaczego 2,5%? Pamiętajmy, że skoro operujemy krótkoterminową roczną średnią, to znaczy, że są to oczekiwania na rok naprzód - a przecież rentowność nie wzrośnie w ciągu roku o nie wiadomo ile. Dlatego przyjmiemy te dwa przykładowe poziomy.

W sumie podstawimy do rozwiązania na x1 i x2 następujące dane:
Rm = 8,7%
SD(M) = 16,1%
Rf = 2,5% lub 3%

Dostaniemy:
*Dla Rf = 2,5%:
x1 = 0,76
x2 = 11,56

x2 odrzucamy, czyli właściwy udział portfela rynkowego w całym portfelu to 1-x = 1-0,76 = 24%.

*Dla Rf = 3%:
x1 = 0,73
x2 = 13,13

Ponownie przyjmujemy x1, czyli udział portfela rynkowego w portfelu to 1-x = 1-0,73 = 27%.

Łącznie dostajemy przedział 25-30% minimalnego udziału portfela rynkowego w portfelu.
W kolejnych przykładach będę odrzucał błędne rozwiązania.


Przykład 2. WIG: 1997-2017.
Średnia stopa zwrotu WIG wyniosła 10,6%, odchylenie standardowe 25,4%, a SDs = 27,5%. Ponieważ:
a) można powiedzieć, że również dla polskiego indeksu odchylenie standardowe jest zbliżone do średniej straty,
b) dla Polski całkowita liczba danych to 21, a do obliczenia SD(M)s posłużyło zaledwie 6 danych (bo tylko 6 lat w ciągu tych 21 było ujemnych...),
to rozsądne jest zastąpić tutaj SD(M)s samym odchyleniem standardowym, D(M).

Teraz kwestia Rf. Krótkoterminowe obligacje skarbowe obecnie są nieopłacalne, skoro proponują ledwo ponad 2%. Banki proponują 2,5-3%. Ponieważ średnia jest większa, przyjmę dla Polski Rf = 3% i 3,5%.

W sumie podstawiamy:
Rm = 10,6%
SD(M) = 25,4%
Rf = 3% lub 3,5%

Dostaniemy:
*Dla Rf = 3%:
x = 0,84

*Dla Rf = 3,5%:
x = 0,82

Zatem dla pierwszego przypadku udział indeksu w portfelu powinien wynieść 1-0,84 = 16%, a dla drugiego przypadku 1-0,82 = 18%.

Z tego przykładu wynika, że powinniśmy trzymać WIG w proporcji 15-20% w stosunku do aktywów bez ryzyka rynkowego.


Przykład 3. Teoretyczny portfel akcji.
Model można uogólnić w ten sposób, że zamiast indeksu, przyjmiemy własny portfel akcji, który uważamy za lepszy od samego indeksu. Wtedy za Rm i SD(M) podstawiamy Rw i SD(W) - odpowiednio oczekiwaną stopę zwrotu z portfela akcji (albo innych ryzykownych aktywów) i średnią potencjalną stratę z tego portfela. Te wielkości podstawiamy do wzoru na x.

Powiedzmy, że znaleźliśmy portfel akcji, który daje Rw = 15% i SD(W) = 20%. Wtedy, przy założeniu Rf = 3%, uzyskamy x = 68%, czyli posiadając tak dobre akcje, powinniśmy je trzymać w udziale co najmniej 32%. Z kolei dla Rw = 15% i SD(W) = 25%, poziom ten spada do 1-x = 21%.

Gdyby natomiast Rw = SD(W), tj. oczekiwany zysk portfela akcji zrównałby się ze średnią stratą z tego portfela, oraz
* Rw = 10%, to 1-x = 78%,
* Rw = 15%, to 1-x = 65%,
* Rw = 20%, to 1-x = 55%, 
* Rw = 25%, to 1-x = 47%.

Podsumowanie:
Z teorii finansów wynika, że portfel rynkowy jest najbardziej zdywersyfikowanym portfelem wśród portfeli ryzykownych, tzn. ma najniższe ryzyko przy danym poziomie oczekiwanego zysku. Portfel rynkowy przybliżamy najczęściej indeksem giełdowym. Stąd inwestor posiada początkowo dwie skrajne możliwości: inwestowanie bez ryzyka albo w indeks giełdowy. Spośród tych dwóch skrajności może wybrać koszyk pośredni. Jeśli będzie chciał trzymać portfel akcji tylko w takiej proporcji, aby potencjalna strata została skompensowana przez oczekiwany zysk, to uzyska pożądany udział portfela, stosując przedstawiony wzór na x.
Jeśli za portfel rynkowy uzna indeks USA, to powinien trzymać 25-30% tego indeksu. Jeśli przyjmie WIG, to powinien go trzymać w udziale 15-20%.
Wiemy jednak obecnie, że klasyczna teoria finansów nie wystarcza. Dlatego inwestor ma szansę znaleźć lepsze, choć bardziej skomplikowane portfele akcji niż indeks. Gdyby znalazł taki, co ma odchylenie standardowe takie samo jak WIG (tj. 25%), ale oczekiwaną stopę zwrotu nie 11, a 15%, to jego udział powinien wynieść 20%. Gdyby udało mu się zmniejszyć jeszcze to odchylenie do 20%, to udział powinien wzrosnąć do 32% (przy Rf = 3%.). W sumie można więc powiedzieć, że minimalny udział akcji w portfelu inwestora powinien się mieścić między 15 a 30%.


P. S. Zasada Pareto 20:80? Do przemyślenia...

Jak prawidłowo obliczać procenty składane dla niepewnych aktywów?

Różni analitycy kuszą ludzi inwestowaniem na giełdzie, przedstawiając im zasadę działania procentu składanego. Najnowszy wpis z tej serii pojawił się dziś na blogu https://pokonacgielde.blogspot.com/2018/04/efekty-procentu-skadanego-w-dugim.html. W tym przypadku autor dodatkowo błędnie przypisuje siłę inflacji do napędzania giełdy. W artykule Czy inflacja jest dobra dla akcji?  podałem dowody empiryczne, że stopy zwrotu są ujemnie skorelowane z inflacją. Ale to akurat osobny temat.

Zastanawialiście się kiedyś czy do procentu składanego wyznaczającego przyszły zysk brać średnią arytmetyczną czy geometryczną? Intuicyjnie wydaje się, że geometryczna jest poprawniejsza. Nie jest to do końca prawda. Gdyby oczekiwana stopa zwrotu była znana (a stopy zwrotu niezależne od siebie), to powinniśmy stosować średnią arytmetyczną. Gdy mamy do czynienia z lokatami, to średnia arytmetyczna staje się równa średniej geometrycznej i dlatego obydwa podejścia są tożsame. Sytuacja się zmienia na instrumentach ryzykownych. W tym przypadku oczekiwana stopa zwrotu może być znana albo nieznana. Jeśli jest znana, to, jak wyżej napisałem, stosujemy średnią arytmetyczną. Jeśli jest nieznana - jak to ma miejsce najczęściej na rynkach - sytuacja się komplikuje. W uproszczeniu, gdy mamy do czynienia z niepewnością, porada jest następująca:
* jeśli interesuje nas krótki okres czasu, to nadal stosujemy średnią arytmetyczną,
* jeśli interesuje nas średni okres czasu, to stosujemy średnią ważoną ze średniej arytmetycznej i geometrycznej,
* jeśli interesuje nas długi okres czasu, to stosujemy średnią geometryczną,
* jeśli interesuje nas bardzo długi okres czasu, tak długi, że przekracza długość próby historycznej, to stosujemy "ukaraną średnią geometryczną" z powodu niepewności co do przyszłości.

Przypomnę, że w artykule W poszukiwaniu nieznanej wartości oczekiwanej - część 1 przeprowadziłem cały dowód (na podstawie rozumowania Blume'a), że w przypadku, gdy nie znamy krótkookresowej oczekiwanej stopy zwrotu, długookresowa oczekiwana stopa zwrotu brutto (tj. zwykła, netto, po powiększeniu o 1) w przybliżeniu będzie dana wzorem:

(1)

gdzie:
T - okres przeszłości; liczba obserwacji do próby
N - okres przyszłości
A - średnia arytmetyczna stopa brutto (liczona dla danych z okresu T). Zapisalibyśmy ją A = 1 + a, gdzie a to średnia arytmetyczna netto, czyli zwykła średnia średnia arytmetyczna.
G - średnia geometryczna stopa brutto (liczona dla danych z okresu T). Zapisalibyśmy ją G = 1 + g, gdzie g to średnia geometryczna netto, czyli zwykła średnia średnia geometryczna.


Przykład: PEKAO SA (PEO).
Okres: od końca 2007 do końca 2017 r., czyli T = 10. Dane roczne ze stooq.pl, który uwzględnia dywidendy, tzn. stopy zwrotu są powiększone o dywidendy brutto. Uzyskane parametry to:
a = 1,08%
A = 1,0108
g = -0,68%
G = 1-0,0068 = 0,9932

* Jeżeli interesuje nas krótki okres, to N = 1 i wtedy wzór (1) sprowadza się do M = A. Czyli rzeczywiście dostajemy średnią arytmetyczną, tj. m = a = 1,08% rocznie.

* Jeżeli interesuje nas średni okres, np. N = 5, wtedy wzór (1) daje M^5 = 1,0157, czyli roczna oczekiwana stopa netto wynosi m = 1,0157^(1/5) - 1 = 0,3% średniorocznie.

* Jeżeli interesuje nas długi okres, np. N = 10 i wtedy wzór (1) sprowadza się do M = G. Czyli rzeczywiście dostajemy średnią geometryczną, tj. m = g = -0,68% rocznie.

* Jeżeli interesuje nas bardzo długi okres, np. N = 20, wtedy wzór (1) daje M^20 = 0,46, czyli roczna oczekiwana stopa netto wynosi m = 0,46^(1/20) - 1 = -3,8% średniorocznie.

Ogólnie biorąc N > T powoduje, że stopa zwrotu jest coraz mniejsza w sposób sztuczny, bo zostaje ukarana za to, że chcemy szacować przyszłość, nie mając wystarczającej liczby danych. Dlatego zalecałbym, aby maksymalnie N = T. Co de facto oznacza, że dla długich okresów czasu stosujemy rzeczywiście średnią geometryczną.

Gdyby występowało ryzyko inwestycji, ale ogólnie roczna oczekiwana stopa zwrotu byłaby znana, to wzór (1) sprowadziłby się do M = A.
(Łatwo zauważymy, że tak będzie, gdy spojrzymy na formułę nr (4) z artykułu, gdzie wyprowadzałem ten wzór - losowy czynnik e(t) wyniesie 0, więc M musi sprowadzić się do średniej arytmetycznej).

I teraz powrócę do tego wpisu bloga, gdzie autor propaguje rachunek procentu składanego. Autorowi wyszła roczna oczekiwana stopa zwrotu PEO równa 6,7% w przeciągu 30 kolejnych lat. Ogólnie teraz widać, gdzie popełnia on błąd (zakłada, że prawdziwa oczekiwana stopa M jest znana) ale zwrócę uwagę na dodatkowy aspekt. Otóż popełnił teoretyczny błąd polegający na włączeniu inflacji do geometrycznej stopy zwrotu. Stopa inflacji to średni wzrost cen z roku na rok. Czyli z punktu widzenia wzoru (1) jest to wzrost 1 rok naprzód. Jeśli podstawimy N = 1, to dostaniemy M = A. Oznacza to, że stopa inflacji wyraża średnią arytmetyczną stopę wzrostu. Ale w takim razie, aby obliczyć M dla PEO autor nie mógł szacować 30 lat naprzód, tj. nie mógł użyć N = 30, a tylko 1. Przypominam, że użycie średniej arytmetycznej jako składanej oczekiwanej stopy zwrotu jest możliwe tylko w trzech sytuacjach:
- oczekiwana stopa zwrotu jest znana,
- N = 1
- T jest bardzo duże, a N niewielkie w stosunku do T. Np. jeśli T = 1000, a N = 10, to z (1) wynika, że M będzie praktycznie równe A.

Nawet jeśli przyjmiemy, że oczekiwana stopa inflacji jest znana (ok. 2%) i wówczas moglibyśmy obliczyć długookresową oczekiwaną stopę inflacji za pomocą średniej arytmetycznej, to już oczekiwana stopa zwrotu z akcji jest nieznana, więc nie możemy połączyć tych dwóch stóp ze sobą. To są po prostu dwie różne kategorie.

Z drugiej strony ktoś zapyta tak, dlaczego nie można uwzględnić inflacji, przecież jeśli przyjmiemy równowagową wersję stopy zwrotu, tj. CAPM, to właśnie powinniśmy ująć inflację, która zawiera się w stopie wolnej od ryzyka, a ta z kolei siedzi w CAPM. To prawda, możemy przyjąć dwa modele jednocześnie: formułę (1) oraz CAPM. One się nie kłócą. Tylko że aby się one ze sobą zgadzały, to CAPM musi także stanowić nieznaną oczekiwaną stopę zwrotu, a skoro powiedzieliśmy, że inflacja siedzi w CAPM, to ta inflacja musi zostać przekształcona w nieznaną oczekiwaną inflację. Ponieważ nieznaną wartość oczekiwaną wyraża wzór (1), to znaczy, że inflacja także musi jemu podlegać. W sumie musimy posiadać dwa rodzaje stóp inflacji: krótkookresową - arytmetyczną oraz długoookresową - geometryczną. Obie byłyby potrzebne do użycia modelu (1). W tym sensie CAPM zostaje podzielony na dwie części: krótkookresową i długookresową. Część krótkookresowa dotyczy średniej arytmetycznej, a długookresowa - geometrycznej.

Nie zawsze da się prosto wyliczyć średnią geometryczną. Normalnie, gdy mamy same stopy, jak w przypadku inflacji, to dodajemy do każdej wartości 1, aby uzyskać stopy brutto, a następnie używamy np. formuły Excela na średnią geometryczną. Sprawa się komplikuje w przypadku zysków, które nie rzadko stają się ujemne. Wtedy nie możemy obliczyć średniej geometrycznej w taki sposób.  Zamiast tego możemy wykorzystać przybliżenie na geometryczną stopę zwrotu, które tutaj wyprowadziłem (nie mylić oznaczeń: w tamtym A to tutaj a). Wzór (1) będzie poprawny dla rozkładu normalnego, toteż ze 4-ch wyprowadzonych przybliżeń, G2 powinien być najlepszy. Przy założeniu normalności rozkładu:

(2)

gdzie V - wariancja.
Częściej interesuje nas odchylenie standardowe, stąd (2) zapiszemy:

(3)

gdzie S - odchylenie standardowe z próby.

Aby wstawić tę formułę do (1), zapiszemy:

(4)

Wstawimy (4) do (1):

(5)

W ostatnich 10 latach (T = 10) średnia inflacja (a) wyniosła 2,02%, tj. A = 1,0202, a odchylenie standardowe (S), 2,03% (Bank Światowy). Podstawmy te dane dla różnych N, aby uzyskać wgląd w oczekiwania na temat inflacji:
* dla N = 1, m = 2,02% = średnia arytmetyczna inflacji,
* dla N = 5, m = 2,01%,
*dla N = 10, m = 2% -> jest to przybliżona średnia geometryczna inflacja,
*dla N = 20, m = 1,98%
*dla N = 30, m = 1,95%.

Jedynie krótkookresowy wzrost, dla N = 1, pozwala na zastosowanie zwykłej średniej stopy inflacji. Dla dłuższych okresów, musi ona zostać odpowiednio pomniejszona. W tym przypadku akurat różnica nie jest duża, ciągle to ok. 2%. Jednak w ogólnym przypadku, gdybyśmy chcieli dodać wzrost zysków, proste łączenie arytmetycznego z geometrycznym tempem wzrostu, okazuje się błędne.

Dowód, że wynagrodzenie netto to ok. 70% wynagrodzenia brutto (ciekawostka)

W ramach ciekawostki pokażę, że wynagrodzenie netto to rzeczywiście ok. 70% wynagrodzenia brutto. Chociaż powszechną praktyką jest szacowanie pensji netto na tym poziomie, to jednak z żadnych znanych mi materiałów nie wyczytamy, że jest to prawidłowe podejście. Powiedzmy, że wynagrodzenie brutto pracownika wynosi 4500 zł. Wg kalkulatora Gofin ( https://kalkulatory.gofin.pl/Kalkulator-wynagrodzen,12.html ) wynagrodzenie netto wyniesie wówczas 3201,58 zł. Kalkulator ten przeprowadza następującą analizę:

Na rysunku pogrubione są 3 rodzaje "kosztów": składki na ubezpieczenia społeczne, składka na ubezpieczenie zdrowotne i zaliczka na podatek dochodowy. Aby uzyskać wynagrodzenie netto, odejmujemy te 3 rodzaje obciążeń:

WN = WB - US - UZ - ZP

gdzie:
WN - wynagrodzenie netto,
WB - wynagrodzenie brutto,
US - składka na ubezpieczenie społeczne. Zgodnie z obowiązującymi obecnie przepisami: US = 13,71%*WB
UZ - składka na ubezpieczenie zdrowotne. UZ = 9%*(WB - US) = 9%*WB*(1 - 13,71%) = 9%*86,29%*WB = 7,77%*WB.
ZP - zaliczka na podatek dochodowy. Ogólnie ZP = PD - UP - OUZ.

gdzie:
PD - podatek dochodowy od osób fizycznych. PD = s*(WB - US - KP),
gdzie
s - stawka podatkowa. Obecnie s = 18%,
KP - koszty uzyskania przychodów. Obecnie miesięczne KP = 111,25 zł.

UP - ulga podatkowa. Obecnie miesięczna UP = 46,33 zł.
OUZ - składka na ubezpieczenie zdrowotne podlegająca odliczeniu od podatku. Zgodnie z przepisami OUZ = 7,75%*(WB - US) = 7,75%*WB*(1 - 13,71%) = 7,75%*86,29%*WB = 6,69%*WB.
Jednakże powyższe formuły na ZP i PD nie są precyzyjne. ZP oraz podstawa opodatkowania (WB - US - KP) muszą być zaokrąglone do liczby całkowitej. Czyli w formułach Excela, zapisalibyśmy
ZP = Zaokr(PD - UP - OUZ; 0). Tj. obecnie ZP = Zaokr(PD - 46,33 - 6,69%*WB; 0),
PD = s*Zaokr(WB - US - KP; 0). Obecnie PD = 18%*Zaokr(WB - 13,71%*WB - 111,25; 0) = 18%*Zaokr(WB*(1 - 13,71%) - 111,25; 0) = 18%*Zaokr(WB*86,29% - 111,25; 0).

Czyli:
WN = WB - US - UZ - ZP = WB - 13,71%*WB - 7,77%*WB - ZP = WB*(1 - 13,71% - 7,77%) - ZP = 78,52%*WB - ZP.

Mamy więc dwie części składające się na WN: 78,52% WB oraz ZP.

Ponieważ, jak wyżej wskazałem, ZP powinno być zaokrąglane, to podzielę teraz materiał na dwie części: dokładną (bez przybliżeń) oraz z przybliżeniami.

A) Dokładna:
Na podstawie powyższych wzorów, można zapisać:
ZP = Zaokr(18%*Zaokr(WB*86,29% - 111,25; 0) - 46,33 - 6,69%*WB); 0)

Stąd:
WN = 78,52%*WB - Zaokr(18%*Zaokr(WB*86,29% - 111,25; 0) - 46,33 - 6,69%*WB; 0)

Możemy w Excelu wstawić tę formułę i zastąpić WB = 4500. Powinniśmy otrzymać WN = 3201,4 zł. W stosunku do prawidłowego wyniku 3201,58 zł, jest 18 gr różnicy, co wynika z zaokrągleń na danych. Przedstawione przekształcenia nie uwzględniają koniecznych zaokrągleń do drugiego miejsca po przecinku przy obliczaniu procentu dla każdego elementu.

B) Z przybliżeniami:
Teraz usuńmy zaokrąglenia dla ZP:

ZP = 18%*(WB*86,29% - 111,25) - 46,33 - 6,69%*WB = WB*18%*86,29% - 18%*111,25 - 46,33 - 6,69%*WB = WB(15,53% - 6,69%) - 18%*111,25 - 46,33 = 8,84%*WB - 18%*111,25 - 46,33

Stąd:
WN =  78,52%*WB - (8,84%*WB - 18%*111,25 - 46,33) =  
= 69,68%*WB + 18%*111,25 + 46,33
 
Wynagrodzenie netto stanowi więc niecałe 70% WB plus 66 zł (18%*111,25 + 46,33 = 66,4). Pamiętajmy, że jest to przybliżenie prawidłowego WN, które wynosi 3201,58 zł, podczas gdy po wstawieniu 4500 do przedstawionego wzoru WN wyniósłby teraz 3201,96 . Jednak to przybliżenie jest nieporównywalnie lepsze niż standardowe, uproszczone podejście:
70%*4500 = 3150,
71%*4500 = 3195,
72%*4500 = 3240.

Ponieważ koszty uzyskania przychodów (KP) oraz ulga podatkowa (UP) dość często się zmieniają, to ogólniej, możemy zamiast 70% WB stosować następujący wzór:

WN = 69,68%*WB + 18%*KP + UP. 

Wzór ten jest możliwy, bo nigdzie w przekształceniach nie używałem KP i UP poza tymi miejscami.
Wzór się jednak nieco zmieni, jeśli stawka s będzie inna. Jeśli wrócilibyśmy do starej s = 19%, wtedy nowy wzór wyglądałby tak:
WN = 68,81%*WB + 19%*KP + UP. Dla WB = 4500, KP = 111,25 i UP = 46,33, WN = 3163,92. Faktyczna WN wyniosłaby 3164,58. Oczywiście ciągle stosując 70%, dostalibyśmy zawsze to samo, czyli 3150. Podejście 70% staje się teraz "bardziej prawidłowe" niż 71%, bo pierwsza część (68,81%*WB) została trochę obniżona. W każdym razie pokazałem, że choć zasada 70% nie jest idealna, to ma ona swoje uzasadnienie matematyczne.

Analiza techniczna pokonuje strategię pasywną tylko na niedojrzałych rynkach

Do tytułowego wniosku można dojść po przeczytaniu kilku prac naukowych. Hsu i Kuan [2] skupili się na zbadaniu wielu narzędzi analizy technicznej na DJIA, S&P 500, NASDAQ oraz Russell 2000. Dane objęły okres 1989-2002, z podziałem na in-sample (1990-2000) i out-of-sample. Sprawdzono wiele strategii: reguły filtra (filter rules, FR), średnich ruchomych (moving average, MA), wsparcie i opór (support and resistance, SR), przełamanie kanału / wybicie z kanału (channel break-outs, CB), wskaźnik wolumenu (on-balance volume averages, OBV), strategie momentum w cenie (momentum strategies in price, MSP), momentum wolumenu (momentum strategies in volume MSV), głowę z ramionami (head-and-shoulders, HS), trójkąt (triangle, TA), prostokąt (rectangle, RA), podwójne szczyty i dna (double tops and bottoms, DTB), a także trójkąt rozszerzający (broadening tops and bottoms, BTB). Przetestowano dzienne stopy zwrotu w porównaniu z metodą pasywną (kup i trzymaj). Uwzględniono w tym koszty transakcyjne i usunięto zjawisko "podkradania danych" (data-snooping), które polega na zniekształcaniu wyników, gdy testuje się ciągle kolejne reguły dla tej samej próby (bo dla każdej losowej próbki możemy sztucznie szukać dowolnej reguły tylko po to, aby dopasować ją do danych).  Wyniki badania:

Jedynie AT zastosowana na NASDAQ i Russel 2000 przyniosła ponadprzeciętne stopy zwrotu. Najlepszą metodą dla obydwu rynków okazała się prosta MA(2) z niewielkim filtrem 0,001, tzn. kurs kupna/sprzedaży został przemnożony przez 1,001. Taka strategia przyniosła Nasdaq 38% rocznej stopy zwrotu, miała także wysoki współczynnik Sharpe'a. Dla DJIA i SP 500 wyniki okazały się nieistotne statystycznie (na poziomie ist. 1%).

Ponieważ na tle DJIA i S&P 500, Nasdaq i Russel 2000 były młodymi giełdami, to autorzy konkludują, że efektywność rynku została zachowana na dojrzałych rynkach, natomiast młode giełdy nie zostały jeszcze odpowiednio zdyskontowane.

Kolejni naukowcy potwierdzili powyższe wnioski. Scaillet i Bajgrowicz [5] przetestowali niektóre techniki co [2]: FR, MA, SR, CB, OBV - na danych DJIA na ogromnej przestrzeni czasu 1897-2011. Podzielili ten zakres na kilka podokresów. Po usunięciu data-snooping  i kosztów transakcyjnych, otrzymano wyniki poniżej:

Najważniejsze jest tu spojrzenie na BRC p-value (obliczone na podst testu  Bootstrap reality check White'a, BRC, który uwzględnia data-snooping). Widzimy, że do 1986 r. techniki AT pozwalały skutecznie zarabiać, a po tym roku, wraz z ich rozpowszechnieniem i rozwojem komputerów, straciły całkowicie skuteczność.

Hsu, Hsu i Kuan [3] przetestowali z kolei dwie techniki: MA oraz reguły filtrów dla podobnych giełd co [2]: SmallCap 600 Growth Index Fund (IJT), Russell 2000 Index Fund (IWM), NASDAQ Composite Index Tracking Fund (ONEQ), ale dodatkowo sprawdzono giełdy krajów rozwijających się: MSCI Emerging Market s Index, MSCI Brazil Index, MSCI South Korea Index, MSCI Malaysia Index, MSCI Mexico Index, and MSCI Taiwan Index.
Autorzy podzielili okresy na okres przed wprowadzeniem ETF-ów i po wprowadzeniu ETF-ów na te indeksy. Okresy przed i po wprowadzeniu ETF-ów dla każdej giełdy, prezentuje poniższa tabela:

Okazało się, że po wprowadzeniu ETF-ów AT straciła moc istotności na wszystkich giełdach USA, a więc także NASDAQ (ETF na niego to ONEQ) i Russel 2000 (IWM), które w badaniu [2] wykazały istotność. Natomiast w zagranicznych giełdach okres po wprowadzeniu ETF, spowodował, że tylko 2 z 6 testowanych giełd wykazywało istotne prawidłowości w badanych strategiach AT: MSCI Malaysia Index Fund (EWM) oraz MSCI Mexico Index Fund (EWW). Przed okresem ETF-ów, 4 z 6 indeksów podlegały istotnie sprawdzanym technikom. Wyniki zbiorcze poniżej:

Poza tym z punktu widzenia wskaźnika Sharpe'a zaledwie jeden rynek (EWW) charakteryzuje się ponadprzeciętnością, tzn. stosując AT ryzyko zostało istotnie obniżone w stosunku oczekiwanego zysku tylko na tym jednym rynku. Sugeruje to, że gdy giełda staje się dojrzała, AT przestaje działać, a wprowadzenie ETF-ów niemal całkowicie usuwa jej ponadprzeciętny wpływ na zyski. Ja bym dodał, że chodzi tu także o coraz większe zautomatyzowanie transakcji, które powoduje, że automaty zaczynają ze sobą konkurować.

Czy w polskich warunkach AT działa? Czekaj, Woś i Żarnowski [1] przeprowadzili szerokie badania na 32 polskich spółkach notowanych od 3 kw 1994 do 3 kw 2000, czyli na stosunkowo małej próbie. Sprawdzali najróżniejsze techniki (na danych dziennych), w tym średnie kroczące, filtry i oscylatory. Ustalili, że ogólnie rzecz biorąc, wiele znanych technik zwiększa średnią stopę zwrotu, ale - po odjęciu kosztów transakcyjnych - w sposób nieistotny statystycznie. W przypadku średniej kroczącej najlepszym parametrem było 72 dni (tj. MA(72)), a średnia miesięczna stopa zwrotu wyniosła - po odjęciu prowizji 0,3% - 1,21%. Nieco lepszym okazał się MA(3) z filtrem 2,5% - średnia miesięczna stopa zwrotu to 1,49%. Jednocześnie metoda "kup i trzymaj" przyniosła miesięcznie 0,8%. Ale żadna spółka nie zwiększyła zysku istotnie dla tych reguł. Zdarzyły się natomiast pojedyncze przypadki spółek, które dla innych technik odnotowały ponadprzeciętne zyski. Najlepszym oscylatorem okazał się ROC(2), dla którego przeciętna miesięczna stopa wyniosła 1,52% (przy 0,3% prowizji), podczas gdy metoda kup i trzymaj 0,8%. Dla tej metody 2 spółki dały istotnie ponadprzeciętne zyski. Jednak 2/32 to zaledwie 6%. Z kolei momentum(105) dał najwyższy spośród wszystkich technik miesięczny zwrot 1,7% (po odjęciu prowizji), ale żadna spółka nie wykazała się tutaj istotną poprawą w stosunku do kup i trzymaj (0,8%).

Znalazłem też pracę [6], w której testowano następujące reguły AT dla polskiej giełdy: formację głowy i ramion, odwróconą formację głowy i ramion, formacje podwójnego szczytu („M”) i dna („W”) oraz formacje potrójnego szczytu i dna - dla WIG20 z lat 1999–2005, oraz akcji wybranych spółek, z lat 2000-2005. Należy tu podkreślić, że autor uwzględnił (chyba?) tak samo jak poprzedni autorzy zjawisko podkradania danych, bo wspomina o nim, nazywając je "nadmierną analizą danych". Autor tak podsumowuje wyniki:
"(...) należy stwierdzić, że czynniki, które według analityków technicznych determinują wiarygodność formacji technicznych, albo nie wpływają w istotny sposób na prawdopodobieństwa odwrócenia trendu i wypełnienia prognozy wybicia z formacji, albo efekt ich oddziaływania jest przeciwny do postulowanego w podręcznikach analizy technicznej. Wydaje się więc, że analiza formacji w postaci rekomendowanej przez zwolenników analizy technicznej ma małą wartość prognostyczną."

Ostatnio także Hsu, Taylor i Wang przebadali w szerokim zakresie rynki walutowe, także usuwając zjawisko podkradania danych [4]. Testowano oscylatory, filtry, MA, SR, kanały. Okazało się, że choć wiele technik AT odgrywało na początku pewną rolę, to z czasem nastąpił jej zanik. Przebadano kurs USD vs 30 różnych walut, w tym polski złoty. Całkowity okres badawczy: 1971-2015. Poniższa tabela przedstawia liczbę technicznych reguł z istotną statystycznie nadwyżkową stopą zwrotu, z podziałem na okresy:

Im późniejsze okresy, tym skuteczność AT słabła. Od 2008 r. tylko dwa rynki walutowe wykazywały rzeczywistą nadwyżkę zysku. Rynek USD/PLN okazał się informacyjnie efektywny, tzn. AT została tam zdemaskowana.

Przypomnę, że robiłem także swego rodzaju test wybić z trendów (zob. tutaj) i w prawie wszystkich przypadkach okazały się nieistotne statystycznie, niemniej na pojedynczych spółkach same wybicia miały prawdopodobieństwa empiryczne powyżej 50%.

Z tych wszystkich badań wynika, że analiza techniczna powinna być traktowana z dużą rezerwą.


Literatura:
[1] Czekaj, J., Woś, M., Żarnowski, J., Efektywność giełdowego rynku akcji w Polsce, PWN W-wa 2001;
[2]  Hsu, PH; Kuan, CM, Reexamining the profitability of technical analysis with data snooping checks, 2005;
[3] Hsu, PH; Hsu, YC; Kuan, CM, Testing the predictive ability of technical analysis using a new stepwise test without data snooping bias, 2010;
[4] Hsu, PH, Taylor, M. P., Wang, Z., Technical Trading: Is it Still Beating the Foreign Exchange Market?, 2016;
[5] Scaillet, O., Bajgrowicz, P., Technical trading revisited: false discoveries, persistence tests, and transaction costs, 2012;
[6] Grotowski, M., Zastosowanie modelu logitowego do weryfikacji skuteczności analizy formacji cenowych, 2009.

Krótki komentarz na temat podnoszenia wynagrodzeń polityków, w tym ministrów

W związku z ostatnią aferą nagrodową PIS coraz częściej pojawiają się sugestie, że wynagrodzenia polityków, zarówno wyższego jak i niższego szczebla, powinny być proporcjonalne do średniego wynagrodzenia brutto. Otóż - jeśli chodzi o zwykłych posłów, senatorów itp. - jest niemal dokładnie na odwrót: ich wynagrodzenie powinno być niezmienne w czasie, a co najwyżej korygowane o inflację. Dlaczego? A dlaczego miałoby rosnąć wraz z realnym wynagrodzeniem? Jeśli od stopy wzrostu wynagrodzeń odejmiemy inflację, to dostaniemy wzrost wynikający z produktywności pracy. Czyli wyższe realne wynagrodzenie wynika tylko ze wzrostu produktywności pracy.
Weźmy firmę prywatną: jeśli przedsiębiorca znajdzie sposób na obniżenie kosztów bez obniżania przychodów, to wzrośnie mu zysk i produktywność. Analogicznie, żeby polityk mógł sprawiedliwie dostawać większą pensję, to powinien być w stanie zwiększyć produktywność państwa, w ten sposób, że obniżyłby na stałe ponoszone koszty bez uszczerbku dla państwa. Podkreśliłem "bez uszczerbku dla państwa", bo nie chodzi przecież o zwykłe cięcie budżetu, ale o wartość dodaną. Jednakże aparat państwowy immanentnie charakteryzuje się biurokracją, która blokuje innowacyjność zarządzania jego strukturami.

Nieco inaczej wygląda sytuacja z ministrami. Oni podejmują istotne decyzje, które mogą poprawić lub pogorszyć budżet państwa. Przykładowo mogą ograniczyć przestępczość gospodarczą, zwiększając dzięki temu wpływy budżetowe. Część z tych wpływów może zostać przeznaczona na zwiększenie wynagrodzenia dla ministrów w wyniku zwiększenia produktywności gospodarki. Tutaj traktuje się państwo jak firmę. Można spojrzeć mniej abstrakcyjnie i potraktować urząd sprawowany przez ministra jako zarządzaną przez niego firmę. Skoro zwiększył "zysk", to rozsądne jest (proporcjonalne) zwiększenie pensji.

Wnioski z tego płyną następujące:
1. Podnoszenie płacy minimalnej, aby wyrównać do wzrostu średniego wynagrodzenia jest błędem, bo na wyższe wynagrodzenie należy sobie zasłużyć. Przedsiębiorcy nie będą skłonni płacić ludziom więcej niż na to zasłużyli. Ekonomia nie znosi próżni i dlatego firmy zaczną podnosić ceny, czyli efektem będzie inflacja. Jeżeli z kolei firma funkcjonuje w wysoko konkurencyjnym środowisku i nie będzie mogła sobie pozwolić na podwyższenie cen, to zacznie szukać oszczędności. Sklepy zaczną zwalniać ludzi i zastąpią ich kasami samoobsługowymi, a w przyszłości robotami. Innym, prostszym sposobem, będzie "wyciskanie pracowników jak cytryny". Skoro bowiem mają zasłużyć sobie na wyższą pensję, to muszą wykonać więcej pracy w danym przedziale czasu. Tak czy inaczej, doprowadzi to do wzrostu bezrobocia.
2. Oznacza to, że płaca minimalna powinna być tylko korygowana o inflację. Oznacza to, że dysproporcja między średnim a minimalnym wynagrodzeniem powinna rosnąć i nie powinno się ich wyrównywać.
3. Dwa powyższe punkty odnoszą się analogicznie do wynagrodzenia szeregowych urzędników państwowych. Ich realne wynagrodzenie powinno być stałe w czasie, bo nie zwiększają oni w żaden sposób produktywności gospodarki.
4. Ministrowie mają mniejszy lub większy wpływ na gospodarkę i zostaje to uwidocznione w budżecie państwa. Jeśli swoimi decyzjami, doprowadzili do tego, że różnica pomiędzy wpływami do budżetu a wydatkami z niego, zwiększyła się, np. o x% to ich wynagrodzenie powinno wzrosnąć także o ok. x%. Ale - uwaga - to działa w dwie strony. Jeśli pogorszyliby budżet o x%, to powinni też stracić x% pensji. Taki mechanizm byłby z jednej strony motywujący do pracy dla ministrów, z drugiej nikt nie miałby pretensji co do wzrostu wynagrodzeń.
Zauważmy, że zaproponowany system premii nie będzie odpowiadać ani wzrostowi PKB, ani wzrostowi wynagrodzeń w gospodarce. Gospodarka może radzić sobie bardzo dobrze, a budżet źle. Minister nie powinien zarabiać więcej tylko dlatego, że "gospodarka kwitnie".

Jak rzetelnie sprawdzić czy dana strategia działa?

Ostatnio napotkałem taki artykuł na bossafx.pl: Czy analiza techniczna może być skuteczna?, który tematycznie przypomina mój artykuł z 2011 Czy analiza techniczna działa? . Chociaż to tylko dwa przykłady, to ilustrują one niespójność podejść do tego samego problemu. O ile bossa zastosowała test serii, który testuje po prostu niezależność kolejnych obserwacji, to ja użyłem schematu Bernoulliego, który pozwala wykryć systematyczność powtarzania się danego zjawiska. Niestety czytelnik w ten sposób traci jasność, który sposób jest poprawniejszy. Odpowiedź jest prosta: moje podejście jest poprawne, natomiast bossy błędne. Jeśli mówimy akurat o analizie technicznej, to liniowa autokorelacja czy to stóp zwrotu czy to samych ich znaków, nie jest istotna dla AT. Przykładowo: wsparcia, opory, punkty odbicia lub formacje w ogóle nie pociągają za sobą konieczności jakichkolwiek autokorelacji. Mogą się pojawić spontanicznie pomiędzy przypadkowymi ruchami, a gdy się pojawią, to ich natura jest nieliniowa. Dlaczego więc bossa stosuje niewłaściwy test dla AT? Wydaje mi się, że to wynika z takiego prostackiego rozumowania:
1) test serii to test na sprawdzanie losowości procesu,
2) jeśli AT działa to znaczy, że zmiany są nielosowe.
Wniosek: jeśli test serii nie wykrywa zależności, to AT nie działa, a jeśli wykrywa, to działa. Oczywiście to jest kompletny nonsens i pomieszanie z poplątaniem. Nielosowość ma różne wymiary, a test serii wykrywa tylko ten najprostszy, podobny do zwykłej autokorelacji. Test serii wykrywa czy powtarzających się serii nie jest za dużo albo za mało w stosunku do rozkładu normalnego czy dwumianowego.

Jeżeli formacje AT nie są zwykłym złudzeniem, to odkryć je mogą tylko zaawansowane metody, jak np. sieci neuronowe, które są w stanie wychwycić nietrywialne wzory. Prostszym i bardziej dostępnym narzędziem jest także regresja nieparametryczna.

Ale chciałem mówić nie o samej AT, ale szerzej o tym jak wszystkie strategie oceniać w kontekście skuteczności. Oczywiście jest to tylko mały wycinek problemu selekcji, ale warto go poruszyć. Otóż wspomniałem na początku o schemacie Bernoulliego. Schemat ten to po prostu taka zbiorcza statystyka sukcesów i porażek danej strategii. Głównym pomysłem, od którego zaczynamy, jest początkowe (racjonalne) założenie, że wyniki sprawdzanej strategii są czysto przypadkowe, tzn. prawdopodobieństwo jej sukcesu jest równe prawdopodobieństwu porażki, a więc wynosi 50%. Ten pomysł przenosimy do rzeczywistości empirycznej w taki sposób: przetestowaliśmy naszą strategię na jakimś walorze i okazało się, że na 27 przypadków wystąpienia reguły (strategii), 19 z nich sprawdziło się. Przykładowo, nasza strategia to kupienie waloru, gdy zostanie przebita linia trendu spadkowego. Sukces to sytuacja, gdy po przebiciu kurs dalej rośnie. Porażka to sytuacja, gdy linia została przebita, ale kurs za chwilę się cofnął i dalej zaczął spadać. W naszym teście wystąpiło 27 linii trendu spadkowego (np. o długości co najmniej 2 miesiące jak w moim teście), która została w końcu przebita. Sukcesem było to, że 19 razy kurs przebił tę linię i dalej rósł. W pozostałych przypadkach po przebiciu wrócił do spadków. Przypominam, że zakładamy od początku, iż wszystkie sukcesy i porażki są tu przypadkowe, tzn. każde zdarzenie ma szansę 50%.
Kolejnym ważnym punktem jest pytanie, ile wynosi prawdopodobieństwo, że wystąpi dokładnie 19 przypadkowych sukcesów na 27 prób. Aby je obliczyć należy zastosować wzór Bernoulliego (funkcję  prawdopodobieństwa rozkładu dwumianowego):

(1)

W naszym przypadku p = 1/2, k = 19, n = 27. Po podstawieniu dostaniemy P(27) = 1,65%.

Na 27 prób 19 przypadkowych sukcesów (tj. 19/27 = 70% obserwacji) może się udać z prawdopodobieństwem 1,65%. Kolejnym krokiem jest sprawdzenie hipotezy zerowej czy ta szansa jest rzeczywiście przypadkowa, jak to od początku zakładamy. Musimy podjąć decyzję czy 1,65%  to dużo czy mało. Jak? Porównujemy uzyskane p-value, tj. wartość dystrybuanty rozkładu dwumianowego, z założonym poziomem istotności. Ilustrując prosto sprawę, zacznę od rozkładu Gaussa. Wiadomo, że w rozkładzie normalnym ponad 95% obserwacji znajduje się w zakresie średnia + 2 odchylenia standardowe. Jest to z pewnością powód, dla którego poziom istotności określa się na 5% jako względnie bezpieczne przybliżenie błędu 1 rodzaju, tj. odrzucenia hipotezy zerowej, która jest prawdziwa (w naszym przypadku odrzucono by losowość). Innymi słowy zakres (średnia plus 2 odchylenia standardowe) uznajemy za wystarczający do przybliżenia pełnej losowej zbiorowości (95% przybliża 100%), a to oczywiście  oznacza, że to co leży poza tym zakresem musi stanowić akceptowalny błąd (nieuwzględnienia możliwości wystąpienia pewnych skrajnych, czysto losowych zdarzeń). To znaczy, 5 na 100 zdarzeń czysto losowych będzie na tyle nietypowych, że wydawać się będą nielosowe i dlatego za takie je uznamy - to jest właśnie błąd pierwszego rodzaju.

Rozkład dwumianowy bardzo szybko przekształca się w rozkład normalny, więc 5% istotności jest dla niego też odpowiednie. Czyli 5% jest pewnym punktem odniesienia do porównania przypadkowości sukcesów. Ale nie możemy porównywać poprzednio obliczonego 1,65% do 5%, bo ta pierwsza wielkość to prawdopodobieństwo tylko konkretnej liczby 19 sukcesów, podczas gdy poziom 5% odnosi się do wszystkich teoretycznych, mało prawdopodobnych sukcesów (skoro wszystko poza główną masą 95%, to wszystko). Stąd musimy dostosować nasze obliczenia do tej kumulacji. Wyobrażamy sobie, że nasz test powtarzamy wielokrotnie w innych wymiarach przy ciągle zmieniających się danych giełdowych. Liczba sukcesów będzie się wtedy zmieniać, czasem będzie więcej sukcesów, czasem mniej - ułoży się to losowo. W ten sposób uzyskamy rozkład częstości, czyli empiryczny rozkład prawdopodobieństwa. Rozkładu tego oczywiście nie znamy i nie widzimy, chyba że podzielimy całą próbę n na mniejsze próbki i dla każdej z nich obliczylibyśmy liczbę sukcesów. W ten sposób dałoby się otrzymać rozkład empiryczny. Wtedy jednak powstaje pytanie, w jaki sposób podzielić próbę na podpróby? Tak więc ten problem zostawiamy i umawiamy się, że mamy tylko jedną próbę, którą chcemy porównać z teoretycznym - rozkładem dwumianowym. Mając strukturę tego rozkładu, zadajemy pytanie jakie jest prawdopodobieństwo, że co najmniej 19 sukcesów będzie czysto przypadkowych. Aby odpowiedzieć, należy zsumować wszystkie prawdopodobieństwa wystąpienia k, k+1, k+2, .... n sukcesów, tzn. od 19 do 27. W ten sposób uzyskamy dystrybuantę rozkładu dwumianowego. Najłatwiej to zrozumieć porównując dwa grafy poniżej. Pierwszy to "efekt reguły 2 sigm"* z poziomem 5% istotności na krańcach:

Powyższy wykres to rozkład Gaussa, do którego rozkład dwumianowy dąży wraz ze wzrostem liczby prób, n. Oczywiście ze względu na to, że argumenty są w tym drugim zawsze liczbami całkowitymi (jako liczba sukcesów), to będzie to siłą rzeczy tylko przybliżenie. Drugi wykres to sam rozkład dwumianowy - prawdopodobieństwa dla kolejnej k-tej liczby sukcesów. Im większe k, tym szansa na sukces spada, bo po prostu większa liczba sukcesów staje się mniej prawdopodobna.

Wzór (1) stosujemy dla k = 19... 27 i sumujemy:

Suma to właśnie p-value. Jak powiedziałem wyżej, porównujemy p-wartość z poziomem istotności 5%, tj. 0,0261 < 0,05. Ale co to własciwie oznacza? Na grafie poniżej obydwie wielkości możemy przeanalizować:

5% to teoretyczne (przyjęte) ryzyko odrzucenia "hipotezy przypadkowości" w sytuacji, gdyby była ona prawdziwa. W konsekwencji prowadziłoby to przyjęcia hipotezy alternatywnej, tzn. przyjęcia testowanej strategii, która w rzeczywistości byłaby nieskuteczna. Ale empiryczne ryzyko tego błędu okazuje się niższe od 5%: szansa, że hipoteza zerowa jest prawdziwa wynosi tylko 2,6% - odrzucamy hipotezę, że 19 sukcesów to tylko przypadek. Jest to w zasadzie najważniejsza konkluzja z tej analizy.

Na koniec - w Gretlu całą opisaną procedurę możemy wykonać bardzo szybko. Aby wyznaczyć p-wartość, wchodzimy w Narzędzia -> 'Wyznaczanie wartości p' i wybieramy rozkład dwumianowy. Mamy 3 pola do wpisania. W pierwszym, Prob, wpiszemy dla naszego przykładu 0,5, bo to jest pr-stwo sukcesu dla hipotezy zerowej (czyli losowości). Liczba (wszystkich) doświadczeń = 27. Za wartość wpiszemy liczbę sukcesów danej strategii, tj. 19:

Po akceptacji dostaniemy:

Szybko zauważymy, że wystarczy dodać pierwsze i ostatnie Prob(x): 0,00957865 + 0,0165408 = 0,02611945. To jest dokładnie nasza p-value, które wcześniej ręcznie obliczyłem. Czyli tak samo jak wcześniej ją porównujemy z poziomem istotności i dochodzimy do wniosku, że hipotezę zerową należy odrzucić i przyjąć hipotezę o "zyskowności" strategii.

* To nie do końca jest efekt reguły 2 sigm, bo zauważmy, że zgodnie z tą regułą 5% obserwacji musi rozkładać się na obydwa ogony rozkładu, a nie tylko prawy. W rzeczywistości więc mamy poziom istotności 2,5% po lewej (obszar, gdzie liczba sukcesów jest mniejsza niż przypadek) i po prawej stronie rozkładu (obszar, gdzie liczba sukcesów jest większa niż przypadek). Oznacza to, że powinniśmy zastosować 2,5% zamiast 5% istotności, jeśli badamy hipotezę tylko prawego ogona (test jednostronny). Mimo to używamy 5% na pojedynczym ogonie.

3-miesięczna cykliczność (sezonowość?) WIG

Mimo iż takie testy jak X-12-ARIMA czy TRAMO-SEATS nie wykazują sezonowości w miesięcznych szeregach stóp zwrotu WIGu, to zauważyłem, że analiza spektralna wychwytuje pewną cykliczność, ściślej 3-miesięczną. Wziąłem do sprawdzianu miesięczne dane WIG w okresie 01.2010-03.2018 (stooq.pl):

Stopy zwrotu na pierwszy rzut oka wydają się czysto przypadkowe:

Co więcej, w stopach tych nie występuje w ogóle autokorelacja:

Może trochę zaskakującym być, że test ADF-GLS wskazał niestacjonarność stóp, podczas gdy KPSS czystą stacjonarność. Możliwe, że chodzi tu nie tyle o zmienność średniej, ale wariancji - w artykule Czy oczekiwane stopy zwrotu w ogóle się zmieniają? doszedłem do wniosku, że ADF-GLS wykrywa zmienność (niewarunkowej) wariancji w czasie oraz średniej, podczas gdy KPSS i ADF nadają się wykrywania zmian tylko w wartości oczekiwanej. Wariancja jest jednak kwestią odrębną i nie zajmuję się nią teraz.

Poddałem następnie stopy zwrotu analizie spektralnej. Oto wyniki:

Wyraźnie wybija się tu zaznaczona długość okresu = 2,65 m-cy, ok. 3 miesięcy. Tak wybijająca się wartość wydaje się świadczyć o występowaniu jakiegoś cyklu raz na kwartał. Oczywiście może być to przypadek, bo gretl nie wykonuje testu na istotność statystyczną tej cykliczności. Ale dodatkowo poddałem analizie spektralnej stopy zmian wolumenu WIG, który towarzyszył tym stopom zwrotu. Same stopy zmian wolumenu tak przebiegały:

Zarówno KPSS jak i ADF-GLS wskazał stacjonarność tej zmiennej. Można więc wykonać analizę spektralną. Oto jej wyniki:

W tym przypadku jeszcze wyraźniej wybija się jedna wartość świadcząca o cykliczności w obrotach giełdowych. I gdy spojrzymy na długość cyklu, to okazuje się ona być równa 2,88, czyli znów prawie 3 miesiące. Trudno uwierzyć, żeby to był przypadek.

Same zwroty nie korelują ze zmianami wolumenu. Ale sytuacja się zmienia, gdy porównamy siłę zmian, tzn. wartość bezwzględną albo kwadrat zmiennej. Na przykład kwadrat stopy zwrotu koreluje już z samymi stopami zmian wolumenu na poziomie 26,5% (i jest to istotne stat. przy p-value 1%). Korelacja ta jeszcze się zwiększa, gdy porównamy kwadraty stopy zwrotu z kwadratami zmian wolumenu - wzrasta do 30%.

Tak więc, pomimo iż na WIGu nie występuje miesięczna autokorelacja, to ukrywa się w nim kwartalna cykliczność powiązana z obrotami.

Dość naturalnym staje się pytanie w tym momencie o sezonowość kalendarzową. Sprawdziłem więc strukturę stóp zwrotu w każdym miesiącu oddzielnie. Wyniki zbiorcze można podsumować takim histogramem:

Pamiętajmy, że jest to niewielka liczba danych (poniżej 10-ciu obserwacji dla każdego miesiąca). Najgorszym kwartałem w tym zestawieniu są maj, czerwiec i lipiec (wszystkie ujemne), co chyba nie jest specjalnym zaskoczeniem. Zaznaczyłem w tej "grupie złych" także kwiecień, bo zaskakująco słabo wypadł w badanym okresie. Dodanie tego czwartego miesiąca zostaje jakby skompensowane poprzez odjęcie jednego miesiąca w ostatniej, także słabszej grupie, w której występują tylko 2 miesiące: listopad i grudzień.

P.S. W przedostatnim poście prognozowałem lekką poprawę na WIGu w marcu. Prognoza ta się nie sprawdziła, bo WIG znacząco spadł, niewiele mniej niż w lutym. Dlatego widać, że takie granie pod "sezon" obarczone jest ryzykiem.

Dolnostronna korelacja

Dodatnia korelacja z rynkiem stanowi jeden z czynników ryzyka inwestycyjnego. Możemy mieć super-tanie akcje, które będą spadać tylko dlatego, że cały rynek spada. Albo na odwrót, drogie akcje mogą rosnąć tylko dlatego, że rynek rośnie. Standardowa analiza zakłada, że korelacja z rynkiem jest stabilna i nie zależy od tego czy panuje rynek byka czy niedźwiedzia. Takie podejście okazuje się zbyt uproszczone, wręcz błędne. Bardzo często akcje korelują znacznie silniej podczas bessy niż podczas hossy. Np. Erb et al. [1] przedstawili następujące wyniki korelacji miesięcznych stóp zwrotu między różnymi krajami, z podziałem na korelacje, gdy rynek kapitałowy rośnie w obydwu krajach i spada w obydwu krajach:

Są to dane objęte okresem styczeń 1970-grudzień 1993. W nawiasach kwadratowych podano korelacje bez wyjątkowego października 1987. Przykładowo między rynkiem USA a Niemiec całkowita korelacja wyniosła 0,348. Ale gdy obydwa rynki rosły, korelacja (Up-Up) wyniosła zaledwie 0,086, natomiast gdy oba rynki spadały (Down-Down), korelacja podniosła się do 0,52 (a bez 10.1987 - 0,41).

Powyższe badanie traktowało rynki na równi, co ma znaczenie dla zbudowania odpowiednio zdywersyfikowanego portfela. Bo załóżmy, że mamy możliwość zainwestowania w jakieś kraje. Zamiast brać do analizy całkowitą korelację, moglibyśmy wziąć korelację Down-Down. Wtedy budowa portfela Markowitza wyglądałaby tak samo jak klasyczna, ale zamiast zwykłych średnich stóp zwrotu, użylibyśmy stopy zwrotu Down-Down (tj. ujemnych stóp zwrotu, które odpowiadałyby tym korelacjom) oraz odchylenie standardowe Down-Down. Zauważmy, że w takim podejściu minimalizowalibyśmy nie tylko ryzyko w sensie semiwariancji (Down-Down), ale także wartość bezwzględną z oczekiwanej stopy zwrotu, która byłaby przecież ujemna. Chociaż musiałbym to sam dokładnie sprawdzić, to wydaje mi się, że analiza portfela stałaby się praktyczniejsza, bo nie musielibyśmy wybierać oczekiwanej stopy zwrotu portfela, ale szukalibyśmy największej możliwej, czyli blisko zera. Ale to na inny temat.

Powiedzmy, że w uproszczeniu analizujemy samą korelację, zakładając, że inne zmienne są takie same dla różnych krajów. Na przykład zastanawiamy się czy zainwestować w USA i Niemcy czy też w USA i Francję. Całkowita korelacja jest mniejsza dla pary USA-Niemcy, więc wydaje się ona lepszym wyborem. Ale przecież tylko dla okresu Down-Down niższa korelacja jest korzystniejsza, a już dla Up-Up jest na odwrót (bo mówimy o pozycji długiej). Gdy przyjrzymy się podziałowi korelacji, zauważymy, że para USA-Francja ma większą korelację w okresie Up-Up (0,266) oraz mniejszą w okresie Down-Down (0,483) w porównaniu do USA-Niemcy. Czyli para USA-Francja stałaby się portfelem efektywnym, a para USA-Niemcy nieefektywnym, odwrotnie niż początkowo stwierdziliśmy.

Dla inwestora aktywnego, poszukującego najlepszych inwestycji, ważniejsze od precyzyjnej dywersyfikacji staje się porównanie jego portfela (akcji) z indeksem giełdowym. W takiej sytuacji jego portfel nie będzie traktowany na równi z indeksem / portfelem rynkowym. Trzeba założyć, że aktywa będą podlegały rynkowi w jakimś stopniu. Pytanie brzmi w jakim stopniu? Aby znaleźć odpowiedź, musimy zbadać korelację tego aktywa z indeksem pod warunkiem, że indeks rośnie albo spada. Innymi słowy mamy tu pojedynczą korelację-Up i korelację-Down. Korelację-Down będę nazywał korelacją dolnostronną, a korelację-Up korelacją górnostronną. Najczęściej to korelacja dolnostronna stanowi czynnik ryzyka.

Ang et al. [2] zdefiniowali obydwa rodzaje korelacji następująco:

gdzie pierwsza z minusem to korelacja-Down i druga z plusem to korelacja-Up. Stopa r(i, t) to stopa zwrotu z i-tego aktywa. MKT(t) - market, czyli stopa zwrotu z portfela rynkowego albo indeksu giełdowego. Stopa MKT ma korelować z r(i, t) pod warunkiem, że jest mniejsza (większa) od pewnej wartości, która dla nas będzie równa zero.

Obliczmy całkowitą, dolnostronną i górnostronną korelację dla polskiego rynku. (W Excelu można to zrobić na dwa sposoby. Pierwszy to zapisać w dwóch kolumnach odpowiednio funkcje, wykorzystując funkcję Jeżeli stopa zwrotu z indeksu mniejsza od 0, to odpowiednia stopa zwrotu, w przeciwnym wypadku pusty znak. Z tego wyznaczamy współczynnik korelacji. Drugi sposób to formuła tablicowa).

Test: miesięczne stopy zwrotu w okresie luty 2000 - luty 2018:
1. WIG jako zwykły portfel akcji vs. S&P500 jako portfel rynkowy (MKT):
a) całkowita korelacja = 0,62
b) korelacja-down = 0,6.
c) korelacja-up = 0,28

Jak widać w miesiącach rosnących WIG zachowywał się "słabiej", a w spadkowych mocno korelował z indeksem USA.

Następnie sprawdziłem kilka spółek na tle WIG (jako MKT):.

2. KGHM vs. WIG
a) całkowita korelacja = 0,7
b) korelacja-down = 0,47.
c) korelacja-up = 0,55

3. Amica vs. WIG:
a) całkowita korelacja = 0,5
b) korelacja-down = 0,51
c) korelacja-up = 0,3

4. Budimex vs. WIG:
a) całkowita korelacja = 0,41
b) korelacja-down = 0,33
c) korelacja-up = 0,35

5. Stalexport vs. WIG:
a) całkowita korelacja = 0,38
b) korelacja-down = 0,4
c) korelacja-up = 0,17

6. Lubawa vs. WIG:
a) całkowita korelacja = 0,4
b) korelacja-down = 0,12
c) korelacja-up = 0,31

7. Elzab vs. WIG:
a) całkowita korelacja = 0,37
b) korelacja-down = 0,29
c) korelacja-up = 0,2

Ta pobieżna analiza wskazuje, że spadkom WIGu nie zawsze towarzyszyła większa korelacja z poszczególnymi akcjami, w przypadku Lubawy i KGHM rosnący rynek im sprzyjał. Dodatkowo LBW wydaje się być odporna na spadki rynkowe.

Jednak powyższa analiza to bardzo długi okres czasu. Korelacja może się przecież zmieniać w czasie. Wykonałem te same obliczenia, ale tym razem od 2010 r.

II) Test: miesięczne stopy zwrotu w okresie styczeń 2010 - luty 2018:

1. WIG jako zwykły portfel akcji vs. S&P500 (jako MKT):
a) całkowita korelacja = 0,6
b) korelacja-down = 0,5
c) korelacja-up = 0,47

Całkowita korelacja między WIG a indeksem USA pozostała stabilna, ale dolnostronna nieco spadła, a górnostronna znacznie wzrosła.

2. KGHM vs. WIG
a) całkowita korelacja = 0,66
b) korelacja-down = 0,46
c) korelacja-up = 0,4

3. Amica vs. WIG:
a) całkowita korelacja = 0,38
b) korelacja-down = 0,39
c) korelacja-up = 0,19

4. Budimex vs. WIG:
a) całkowita korelacja = 0,39
b) korelacja-down = 0,09
c) korelacja-up = 0,31

5. Stalexport vs. WIG:
a) całkowita korelacja = 0,29
b) korelacja-down = -0,06
c) korelacja-up = 0,32

6. Lubawa vs. WIG:
a) całkowita korelacja = 0,46
b) korelacja-down = 0,31
c) korelacja-up = 0,2

7. Elzab vs. WIG:
a) całkowita korelacja = 0,33
b) korelacja-down = 0,23
c) korelacja-up = 0,14

Nasuwają się tutaj 2 wnioski. Po pierwsze struktura zmieniła się, tak, że 4 z 6 spółek posiadają teraz większą korelację-down niż korelację-up. Po drugie, zastanawiające są statystyki STX i BDX. Korelacja-down dla STX odwróciła się niemal o 180 stopni, spadając z 0,4 do -0,06, co w istocie znaczy brak korelacji z WIG w okresach spadków. W dodatku korelacja-up znacząco wzrosła. Sugeruje to, że te akcje można trzymać w większym udziale niż inne. Natomiast w przypadku BDX korelacja-up prawie się nie zmieniła, natomiast bardzo spadła korelacja-down. Gdy WIG spadał, BDX prawie nie reagował. Innymi słowy, niezależnie od kierunku indeksu, był to dobry okres dla tej spółki.

Niestety problem, jak widać, polega na tym, że korelacja zmienia się w czasie, co zresztą wykrywały już liczne badania zagraniczne [1, 2, 3, 4, 5] i nie możemy mieć pewności co do tego samego poziomu korelacji w przyszłości. Możemy jednak posłużyć się nowoczesnymi, dynamicznymi modelami, jak np. modelem Engle'a [3], które prognozują ten poziom.

Literatura:
[1] Erb, C. B., Harvey, C. R., Viskanta, T. E., Forecasting International Equity Correlations, Dec. 1994;
[2] Ang, A., Chen, J., Xing, Y., Downside Correlation and Expected Stock Returns, Mar 2002;
[3] Engle, R. F., Shephard, K., Theoretical and Empirical properties of Dynamic Conditional Correlation Multivariate GARCH, Dec 2001;
[4] Wong, A. S. K., Vlaar, P. J. G., Modelling time-varying correlations of financial markets, Sep 2003;
[5] Solnik, B., Boucrelle, C., Fur, Y. L., International Market Correlation and Volatility, Sep. - Oct., 1996.