Krótkookresowa prognoza WIG - na marzec 2018

WIG zaliczył w lutym solidny spadek wartości - niecałe 7%. Jest to powyżej odchylenia standardowego miesięcznej stopy zwrotu 5,8% (w okresie 2006-2017). Może to oznaczać, że indeks powróci do średniej w marcu i kwietniu - są to zresztą statystycznie dobre miesiące dla giełdy. Przeprowadziłem krótką analizę w gretlu w oparciu X-13-ARIMA (zob. Usuwanie sezowości i prognozowanie przy pomocy X-13-ARIMA i TRAMO/SEATS) oraz ARIMAX z inflacją w przemyśle jako zmienną egzogeniczną.

1) X-13-ARIMA dla miesięcznej stopy zwrotu WIG: automatycznie uzyskany trend wygląda następująco:

Wykres sugeruje, że stopa WIG znajduje się poniżej trendu, a sam trend wyprostował się. Dokładna prognoza wg X-13-ARIMA na marzec 2018 to +0,13%.

2) ARMAX dla miesięcznej stopy zwrotu WIG z inflacją w przemyśle m/m jako zmienną egzogeniczną: aby wykonać taką prognozę, należy wykonać trochę więcej obliczeń. Najpierw bierzemy inflację w przemyśle z GUSu (dla okresu 01.2006-01.2018). Dlaczego akurat inflacja w przemyśle? Okazuje się ona ujemnie skorelowana ze stopą zwrotu WIG. Od 2006 r. korelacja między miesięcznym tempem WIG a inflacją przemysłu m/m wyniosła -0,26 (por. z art. Czy inflacja jest dobra dla akcji?). Jest to korelacja istotna stat. na p = 0,01. Oznacza to, że WIG zachowuje się średnio biorąc odwrotnie do inflacji w przemyśle.

Następnie także za pomocą dodatku armax szukam optymalnego ARMA dla samej inflacji przemysłu. AIC wskazał ARMA(2,3), a HQC ARMA(0,1). Który bierzemy pod uwagę? Wg Venus Liew HQC przewyższa wszystkie kryteria, gdy próba jest stosunkowo duża i wynosi co najmniej 120 (dla modelu ARMA) [1]. Przy mniejszej próbie lepszy jest AIC. W naszym przypadku jest ponad 140 danych, czyli korzystamy z HQC. Stąd można wyznaczyć prognozę tej inflacji na luty, marzec:

Teraz możemy wstawić prognozę z lutego i marca do danych, a dodatkowo ustawić zakres próby na 01.2006 - 02.2018, po to, aby gretl uznał marzec za prognozę.

Przedostatnim krokiem będzie optymalizacja modelu stopy zwrotu WIG za pomocą dodatku armax. Poszukujemy modelu ARMAX(p, q) z inflacją przemysłu w roli zmiennej egzogenicznej. Dodatek wskazał optimum dla ARMAX(6, 6) - zarówno dla AIC jak i HQC. Uzyskujemy parametry:

 Ostatni krok to prognoza na marzec:

Stopa w marcu może być więc ciągle ujemna. Ale gdybyśmy wybrali model tylko minimalnie gorszy ARMAX(8, 2):

gdzie HQC jest praktycznie identyczny, to dostalibyśmy prognozę w marcu na plus:

Literatura:
[1] Liew, Venus Khim−Sen,  Which Lag Length Selection Criteria Should We Employ?, May 2004.

Podaż pieniądza a stopy zwrotu z akcji

Podaż pieniądza (M) jest drugą obok PKB wielkością makroekonomiczną, która może oddziaływać na rynek akcji. O ile sprawa z PKB jest oczywista (poprawa koniunktury poprawia zyski firm), o tyle M staje się bardziej tajemnicza. Wiadomo, że zbyt duża podaż pieniądza powoduje inflację, a z kolei inflacja wydaje się być ujemnie skorelowana ze stopami zwrotu (zob. Czy inflacja jest dobra dla akcji?) natomiast zbyt mała podaż wywoła stagnację, tj. spadek aktywności gospodarczej, gdyż brakuje "narzędzia" do wymiany jakim jest pieniądz, np. banki nie udzielają kredytów na inwestycje. Większa ilość pieniędzy może pobudzić płynność na rynkach, powodować, że ludzie będą chcieli zwiększać portfel akcji.

Jak więc wygląda sytuacja u nas? Testy przeprowadziłem w gretlu. Sprawdziłem zależność pomiędzy zmianami procentowymi podaży pieniędzy a stopami zwrotu WIG. Dane (z GUS i stooq.pl) objęły kwartały w okresie 1 kw 2000 - 4 kw 2017. Pokażę najpierw korelogram dla WIG i różnych opóźnień podaży pieniądza:

Zacznijmy od punktu zero: jest to korelacja stóp WIG i M z równoległych okresów, kwartał do kwartału i wyniosła -0,22, co sugeruje delikatną ujemną zależność. Ale popatrzmy co się dzieje dla opóźnień ujemnych od -6 do -10, czyli przyspieszeń M: korelacja staje się silnie dodania. Można na to zjawisko spojrzeć z dwóch perspektyw. Z jednej strony wzrost (spadek) WIG w danym kwartale powoduje, że M wzrośnie (spadnie) po kolejnych 6-10 kwartałach. Wyjaśnienie byłoby takie, że wycena giełdowa  uwzględnia zyski memoriałowe, które przekształcają się po pewnym czasie w żywy pieniądz. Z drugiej strony może być też tak, że WIG antycypuje wzrost podaży pieniądza za 6-10 kwartałów (czyli powiedzmy za 2 lata). Ta druga perspektywa odpowiada idei, że rynek przewiduje większą (mniejszą) aktywność ekonomiczną i dlatego już wcześniej - zgodnie z teorią efektywnego rynku -  podwyższa (obniża) ceny akcji.

Skoro tak, to zoptymalizujmy model ARMA dla podaży pieniądza, aby ewentualnie przewidzieć jej kolejne zmiany. Przeprowadzę następnie prognozę M na kolejne 2 lata, tj. 8 kwartałów, bo to średnia (z 6-10 kwartałów), która powinna wskazać obecny ruch WIG.  Ponieważ jest to prognoza długoterminowa, to przeprowadzę ją dwiema metodami: właściwą metodą największej wiarygodności (MNW) oraz warunkową metodą największej wiarygodności (CMNW) . W artykule
Czy ARMA estymować warunkową metodą największej wiarygodności? argumentowałem, że dla długoterminowej prognozy optymalną metodą może okazać się CMNW. Optymalne modele uzyskałem za pomocą dodatku armax.

 - MNW: optimum to ARMA(0, 8):

- CMNW: optimum to ARMA(1, 4):

Wyniki obydwu metod nieco się różnią. MNW wskazuje, że po dwóch latach nastąpi dość gwałtowny wzrost M. Z kolei CMNW sygnalizuje, że wzrost M wyhamuje (widać, że będzie szczyt w cyklu - analiza spektralna to potwierdza zresztą). Gdyby faktycznie CMNW był poprawniejszy dla długoterminowych prognoz, to WIG może się poddać siłom spadkowym. Siła ta może się wzmocnić w 2019, jeśli po dwóch latach M wejdzie w spadkową falę własnego cyklu. Jeżeli dodatkowo wierzyć, że korelacja rzędu 0 między WIG a M jest naprawdę ujemna, to spadkowa prognoza WIG na 2018 po raz kolejny zostałaby potwierdzona. Osobiście liczę na to, że WIG sumarycznie spadnie w tym roku niewiele, a większy bessowy zjazd objawi się w 2019.

Równanie wymiany Fishera, czyli pieniężne spojrzenie na gospodarkę

Równanie wymiany Fishera określa związek pomiędzy PKB a ilością pieniądza w gospodarce. Jego poznanie pozwala szerzej spojrzeć na gospodarkę - nie tylko przez pryzmat sfery realnej (PKB), ale także pieniężnej. W Internecie raczej ciężko znaleźć wyprowadzenie tego równania, więc wypełnię tę lukę. W rzeczywistości jest to tautologia, ale interpretacja oraz konsekwencje tego równania nie są już oczywiste.

Na poziomie makro przychody, wydatki i dochody to właściwie to samo. Wydatek jest czyimś przychodem. A skoro wydatek staje się przychodem, to sumarycznie koszty nie występują. A skoro tak, to znaczy, że przychody muszą być równe dochodom. Jednocześnie przychody oznaczają jakieś produkty lub usługi, a więc możemy zapisać tożsamość:

Produkty i Usługi = Przychody = Wydatki = Dochody.

Przychody, czyli sprzedaż - oznaczmy s, stanowi iloczyn ceny (p) i liczby sprzedanych produktów (q):
(1)

Dla wszystkich dóbr będzie to zapis sumy:

(2)

gdzie T - liczba wszystkich transakcji kupna/sprzedaży.

Lewą stronę podzielimy i pomnożymy przez podaż pieniądza, którą oznaczamy M, natomiast prawą stronę podzielimy i pomnożymy przez całkowitą ilość (wolumen) produkcji, Q.

(3)

Zapiszmy to w postaci:

(4)

gdzie:

(5)

Wielkość V nazywana jest szybkością obiegu pieniądza. Później wyjaśnię dlaczego to się tak nazywa. Natomiast P jest to po prostu średnia ważona cena w gospodarce.

Równanie (4) to równanie wymiany. Niby banał. Jednakże podstawową ideą nie jest samo jego wyprowadzenie, ale zrozumienie wielkości V w tym równaniu. Z definicji jest to iloraz sprzedaży i podaży pieniądza. Ale co to znaczy? Tutaj musimy sięgnąć do poprzedniego spostrzeżenia, że przychody, czyli sprzedaż równa się wydatkom. Bo teraz możemy spojrzeć tak: posiadamy pewną kwotę pieniędzy (którą reprezentuje podaż pieniądza), którą następnie wydajemy na kupno pewnego dobra. W takim razie podaż pieniądza = wydatki, a wtedy V = 1. Ale jeśli V = 1, to M = P*Q. Czy rzeczywiście jest tak zawsze? Nie. Dochód nie musi opierać się tylko na pieniądzu, dobro może być kupione za inne dobro. Podobnie podaż pieniądza czy ilość pieniądza nie musi automatycznie przekładać się na dochody. Załóżmy, że gospodarka zwiększa ilość pieniędzy, np. Kowalski przyjeżdża do kraju z oszczędnościami z zagranicy. Zwiększa się więc ilość pieniędzy w gospodarce, ale jeszcze nie powstaje dochód. Za pieniądze Kowalski kupuje od Iksińskiego jakieś dobro. Powstaje wydatek u Kowalskiego i przychód u Iksińskiego. Ale powiedziałem wyżej, że wszystkie wydatki w gospodarce tworzą dochód oraz że wszystkie przychody tworzą dochód. A więc w tym momencie powstaje dochód krajowy i ilość pieniędzy faktycznie równa się temu dochodowi. Oznacza to, że pieniądz staje się dochodem dopiero wtedy, gdy nastąpi transakcja. Musi nastąpić wymiana: pieniądz za produkt. Czy w takim razie warunkiem do tego, aby V = 1, jest sytuacja, że każda jednostka pieniężna zostanie wymieniona w transakcji? Odpowiedź jest negatywna.

Przyjrzyjmy się takiemu przykładowi. Kontynuujemy wymianę handlową między Kowalskim a Iksińskim. Po tym jak Kowalski kupił dobro od Iksińskiego, teraz Iksiński chce kupić inne dobro od Kowalskiego - za te same pieniądze, które wcześniej otrzymał ze sprzedaży. Znów więc powstaje wydatek - tym razem dla Iksińskiego oraz przychód dla Kowalskiego. A skoro powstał znowu wydatek i przychód, to musiał powstać znowu dochód! Dochód dosłownie się podwoił. Obie osoby w ogóle nie zwiększyły bogactwa w postaci większej ilości pieniędzy (mają ich tyle ile na początku), ale dochód narodowy się zwiększył. Ta druga transakcja podwoiła dochód z tych samych pieniędzy. Czy nie jest to kuriozalne? Jak to racjonalnie wyjaśnić? Kowalski kupił produkt lub usługę od Iksińskiego, a następnie Iksiński kupił produkt lub usługę od Kowalskiego i w ten sposób wytworzono więcej dóbr. Jeżeli Kowalski kupił np. usługę naprawy traktora, to "naprawa" powstaje dopiero dzięki transakcji jako akt działalności/twórczości ludzkiej. Naprawa niejako zasysa potrzebę gospodarki czy po prostu zaspokaja jej zapotrzebowanie. Następnie, jeśli Iksiński kupuje od Kowalskiego produkt rolniczy, np. kukurydzę, którą ten drugi hoduje, to kukurydza już jako wcześniejszy efekt sadzenia, tj. jako akt pracy ludzkiej, również staje się produktem, który zaspokaja potrzeby gospodarki. Powstały dwa produkty o tej samej wartości rynkowej, dlatego dochód stanowi suma tych wartości rynkowych. Dlatego dochód się podwoił mimo iż pieniędzy jest tyle samo.

---------------------------------------
ROZWINIĘCIE TEMATU:
Teraz ciekawska osoba spytałaby co by się stało, gdyby Kowalski najpierw kupił od Iksińskiego jakiś produkt, a następnie Kowalski chciałby sprzedać Wiśniewskiemu ten sam produkt po wyższej cenie? Przecież zgodnie z powyższym schematem, znowu powstają dwie transakcje, pieniądz również dwukrotnie przechodzi z rąk do rąk, ale przecież nie wytworzono nowego produktu. Gdyby dochód miał się podwoić w wyniku sprzedania tego samego dobra dwukrotnie, to nie miałoby to najmniejszego sensu i mielibyśmy do czynienia ze zwykłym oszustwem księgowym. Ekonomiści rozwiązali ten problem w ten sposób, że odejmują od przychodów przedsiębiorstwa te wydatki, które musi ono ponieść na użycie dóbr pośrednich (tj. tych dóbr, które są przetwarzane na dobra finalne). W ten sposób oblicza się tzw. wartość dodaną. PKB tworzony jest właśnie przez wartość dodaną (powiększoną o podatki od produktów i pomniejszoną o dotacje od produktów - zob. GUS, metodologia obliczeń, np. w Rocznikach Statystycznych). Pokażmy to na przykładzie w etapach:

1. Kowalski kupuje dobro po x zł od Iksińskiego: na tym etapie wartość dodana = x. Wyjaśnienie: powstaje przychód, który stanowi jednocześnie koszt równy x. Nie ma tu jeszcze dobra pośredniego.

2. Wiśniewski kupuje od Kowalskiego to samo dobro po (x+r) zł: wartość dodana na tym etapie wynosi: x + (x+r) - x = x + r. Wyjaśnienie: pierwszy element wartości dodanej x zł powstał w pierwotnej transakcji z pktu 1. W drugiej transakcji powstaje przychód dla Kowalskiego, który stanowi jednocześnie koszt Wiśniewskiego, x+r. Ale skoro Kowalski sprzedaje dobro, to jest to dobro finalne. Ale skoro powstało dobro finalne, to trzeba uwzględnić dobro pośrednie - Kowalski poniósł koszt dobra pośredniego w wys. x zł (nieważne, że to jest to samo dobro). To znaczy, że powstaje koszt pośredni x zł, który musimy dodatkowo odjąć. I dlatego sumarycznie wartość dodana wynosi x+r. Jest to sumaryczna wartość produktów finalnych w gospodarce i kreuje PKB po pewnych korektach.
---------------------------------------

Dochód powstaje poprzez stworzenie produktu, a produkt powstaje dzięki kapitałowi ludzkiemu, tj. zdolności do wykonania pracy. W fizyce energię definiuje się właśnie w ten sposób. Oznacza to, że kapitał to energia. Kapitał w danej jednostce czasu staje się dochodem (PKB). A ponieważ dochód równa się ilości pieniędzy (M) pomnożonej przez V, a w fizyce zgodnie ze wzorem Einsteina energia równa się masie pomnożonej przez prędkość światła w próżni, to znaczy, że podaż pieniądza razy V możemy utożsamić z masą pomnożoną przez prędkość światła. W sumie dostajemy taką analogię:

E = mc^2
PKB = MV

Stąd domyślamy się, że M to masa, a V staje się analogią do c^2. Rzeczywiście V została nazwana szybkością obiegu pieniądza. Interpretuje się ją jako liczbę transakcji, w których wzięła udział jedna jednostka pieniężna w danym okresie. Czyli ile razy pieniądz został wymieniony w jednostce czasu.

Powyższa analogia to mój pomysł, nie ma to związku z prawdziwą historią ekonomii. Fisher pokazał swoje równanie znacznie wcześniej niż Einstein, więc to nie tak, że nazwał V szybkością, aby zachować tu specjalnie analogię. Ale to podobieństwo formuł pozwala lepiej przyswoić równanie wymiany.

Wracając do ekonomii, właściwie dlaczego tak naprawdę V interpretuje się jako szybkość obiegu pieniądza? Z matematycznej definicji V (wzór 5) to nie wynika. Podałem wcześniej prostą ilustrację, w jaki sposób dochód przekracza podaż pieniądza, gdy tylko wzrasta liczba transakcji, którym towarzyszy rosnąca ilość produktów lub usług. Mieliśmy 2 transakcje. Po pierwszej V = p*q / M. Po drugiej V = (p*q + p*q)/M. Ale w naszym przykładzie q = 1, tj. jeden produkt. Czyli V = (p + p) / M = 2p/M. Ale przecież M w naszym przykładzie równa się p. Czyli V = 2p / p = 2.

Powiedzmy teraz, że q > 1. Czy to coś zmienia? Przecież początkowo Kowalski wydał p*q pieniędzy, a to znaczy, że M = p*q. Powiedzmy, że Kowalski kupił od Iksińskiego q1 dóbr po p1. Następnie Iksiński kupił od Kowalskiego q2 dóbr po p2. Ale założyliśmy przecież wcześniej, że Iksiński wydaje te same pieniądze, co zarobił. Oznacza to, że p1q1 = p2q2. Czyli możemy znów obliczyć:

I to jest właśnie szybkość obiegu pieniądza: 2 transakcje w danym okresie czasu.

Przytoczony przykład jest trochę mylący, bo T = V = 2. Sugeruje on, że liczba transakcji T (albo dóbr, Q) jest zawsze równa V. Kolejny przykład pozwoli już nam zauważyć, że tak być nie musi. Pozwoli też w pełni zrozumieć czym jest szybkość obiegu pieniądza. Pochodzi on z angielskiej Wikipedii  (Velocity of money):

Przykładowo, w bardzo małej gospodarce, farmer i mechanik, mając zaledwie 50 USD, kupują od siebie nowe towary i usługi w zaledwie trzech transakcjach w ciągu roku:

     Farmer wydaje 50 dolarów na naprawę ciągnika od mechanika.
     Mechanik kupuje od rolnika kukurydzę za 40 dolarów.
     Mechanik kupuje od rolnika sałatę za 10 dolarów.
 
Najpierw policzmy z definicji V:
M = 50 $. Mamy 3 dobra, czyli T = Q = 3. Pierwsze dobro zostało kupione po 50 $, drugie po 40 $ i trzecie po 10 $. Czyli ze wzoru (5) mamy V = (1*50$ + 1*40$ + 1*10$) / 50$ = 2.

A zatem w tym przypadku T = 3, a V = 2. I teraz pewne spostrzeżenie, które pozwoli nam łatwo zrozumieć definicję "szybkości obiegu pieniądza". Zamiast początkowych 50 USD, moglibyśmy użyć 2 USD, bo wtedy nie zmieni się V. A wtedy możemy krok po kroku przestudiować co się dzieje z każdą jednostką dolara. Popatrzmy na ten schemat:

Od razu widać, że 1 dolar musi przejść dokładnie 2 razy z rąk do rąk mimo iż występują 3 transakcje. Jeden dolar przechodzi najpierw do mechanika (1 transakcja), a potem wraca do farmera (2-ga transakcja). W 3-ciej transakcji, gdy dolar wraca od mechanika do farmera, bierze udział już inna jednostka dolara.
Im większa będzie całkowita kwota, tym więcej będzie transakcji (mechanik kupi więcej dóbr), natomiast szybkość obiegu pieniądza pozostanie stała - jeden dolar będzie brał udział ciągle w dwóch transakcjach, bo przecież nie może się rozdzielić na ułamki. 

Zatem szybkość obiegu pieniądza V mówi w ilu transakcjach jedna jednostka pieniężna została użyta w danym okresie. Czyli ile razy pieniądz został wymieniony w jednostce czasu.

Wydaje się to wszystko jasne. Ale w sumie taka prosta analiza doprowadziłaby do konkluzji, że V zawsze równa się 2. Bo popatrzmy: dla naszego przykładu V zdefiniowalibyśmy następująco:

V = (p1*q1 + p2*q2 + p3*q3) / M

Jednocześnie wiadomo, że M = p1*q1, bo wydane na początku pieniądze, które się pojawiają w gospodarce nie zmieniają się. Czyli:

V = (p1*q1 + p2*q2 + p3*q3) / (p1*q1).

Dalej, wiadomo, że nie powstają tutaj w ogóle oszczędności, tj, wszystko co zarobione na sprzedaży jest wydawane. Czyli p1*q1 = p2*q2 + p3*q3. Stąd:

V = (p1*q1 + p1*q1) / (p1*q1) = 2p1*q1 / (p1*q1) = 2.

Szybko zauważymy, że nie ma znaczenia ile mechanik by kupił dóbr od rolnika, zawsze wyjdzie tutaj V = 2.

Faktycznie, ale tylko dlatego, że w gospodarce są tylko dwie osoby i na dodatek nie handlują już niczym innym. Wystarczy, że farmer znów kupi jakąś usługę u mechanika za te same pieniądze, wówczas T = 4, a V = 3. Tak samo jak wcześniej p2*q2 + p3*q3 = p1*q1. Ale już p4*q4 to kwota, która powróciła do farmera, czyli jest równa p1*q1. Ponieważ M nie zmienia się, to wynosi ciągle p1*q1. Czyli dostajemy:

V = (p1*q1 + [p2*q2 + p3*q3] + p4*q4) / M = (p1*q1 + p1*q1 + p1*q1) / p1*q1 = 3.

Wtedy pieniądz rzeczywiście zaczyna szybciej krążyć. Równie dobrze może się pojawić na rynku szewc. Jeśli farmer właśnie "zarobił" (tak naprawdę nie zarobił, tylko dostał z powrotem) 2 dolary, to może od szewca kupić buty (czy może raczej sznurówki). Automatycznie powstałaby czwarta transakcja oraz V = 3. Gdyby następnie szewc kupił od farmera sałatę, to T = 5 i V = 4. Ale ponieważ ilość pieniędzy się nie zmieniła, a każda transakcja wymiany oznacza powstanie dochodu, to znaczy, że dochód zwiększył się 4-krotnie w stosunku do podaży pieniądza.
Teraz czujemy na czym to polega. Podaż pieniądza stanowi punkt zaczepienia dla PKB na początku okresu.

To teraz wróćmy do skali makro. Przecież powiedzieliśmy, że przychody = dochody = PKB. Oznacza to, że (4) możemy w formie:

(6)

Nominalny PKB jest równy podaży pieniądza przemnożonej przez szybkość obiegu pieniądza. Popatrzmy na poniższy wykres PKB nominalnego i całkowitej podaży pieniądza w okresie 1 kw 2002-3 kw 2017:

Źródło: GUS.

 Wówczas całkowita szybkość obiegu pieniądza, V = PKB / M kształtuje się następująco:

 

Źródło: GUS.

Czyli V jest ułamkiem i w dodatku spada. Dlaczego? Są tu dwa aspekty. Po pierwsze  są dwa rodzaje podaży pieniądza: pieniądz gotówkowy w obiegu oraz pieniądz depozytowy. W gospodarce oczekiwalibyśmy, żeby V > 1, bo każda jednostka pieniężna powinna obsłużyć wiele transakcji wymiany. Jednak w systemie depozytowym mamy do czynienia z dwoma efektami. Jeden - będą tworzone duże rezerwy oszczędności. Drugi - pieniądz może być jak gdyby kreowany przez bank. Osoba A lokuje pieniądze w banku, a bank, wierząc, że ta osoba nie wycofa szybko pieniędzy, może pożyczyć osobie B te same pieniądze. Osoba B kupuje za kredyt jakieś dobro od osoby C, a osoba C znów lokuje zarobione pieniądze w banku. W ten sposób bank niejako wykreował pieniądze dla osoby C i ten mechanizm nazywa się kreacją pieniądza.

Jeśli weźmiemy tylko gotówkę w obiegu, to PKB > M i V > 1:

Źródło: GUS.

Wtedy V = PKB nom / (M gotówkowy) ma przebieg:

 Źródło: GUS.

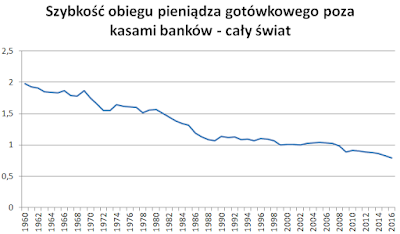
Mimo iż V > 1, to może zdziwić, że V spada niezależnie od tego, którą wielkość przeanalizujemy. Jeśli chodzi o szybkość obiegu pieniądza gotówkowego, to z pewnością znaczenie ma tu wypieranie zwykłego pieniądza przez pieniądz elektroniczny. Ale ogólnie chodzi tu jeszcze o coś innego, bo tendencja spadkowa V dotyczy całego świata -od dziesięcioleci. Popatrzmy:

Źródło: Bank Światowy

Odpowiedź leży w drugim aspekcie, który zasygnalizowałem. PKB jest przecież miarą dochodu uzyskanego w danym okresie, czyli w ciągu roku. Natomiast podaż pieniądza dotyczy całej masy pieniądza w gospodarce. Innymi słowy, podaż pieniądza należałoby prędzej porównywać z aktywami albo kapitałami własnymi. 

Niemniej spadek PKB w stosunku do M oznacza, że masa pieniężna jest za duża w stosunku do wytwarzanego produktu i tym samym kreowana jest inflacja.


Literatura:
Fisher, I., The Role of Capital in Economic Theory, Dec., 1897.

ARMAX opóźnionego WIG z PKB UE - lecimy w dół?

Warto przyjrzeć się jeszcze raz macierzy korelacji między zmianami procentowymi indeksu giełdowego a gospodarką. Tym razem jednak zostawimy już ANNI w spokoju, a zamiast tego dodamy opóźnienie o 1 rok WIG. Pozwoli to przeanalizować dane roczne dla lat 1995-2016 (z Banku Światowego). Wyniki:

Korelacja między WIG(-1) a PKB Polski = 0,41.
Korelacja między WIG(-1) a PKB UE = 0,52.
Korelacja między WIG(-1) a PKB USA = 0,47. 

Ponadto widzimy, że między gospodarkami występuje podobnie silna korelacja. Rozsądne więc - chwytając się brzytwy Okhama - wybrać tylko jedną parę o najsilniejszej korelacji w procesie prognozy. W sumie wystarczy, że do prognozy WIGu weźmiemy o jeden rok przyspieszone PKB UE. Jeśli potrafimy prognozować gospodarkę rok naprzód, to powinniśmy także umieć prognozować WIG.

Dla jasności - podane dane dotyczą realnego PKB na osobę w dolarach US.

Przed prognozą musimy jeszcze spojrzeć na autokorelacje WIGu. Zgodnie z macierzą korelacji, można by przypuszczać, że występuje bardzo słaba ujemna korelacja między kolejnymi latami na giełdzie. Do myślenia daje fakt, że dla zmian opóźnionych o 2 lata wynosi aż -0,35:

Zgodnie z takim schematem indeks po 2 latach zmienia niejako kierunek - odpowiadałoby to długości cyklu: 2 lata w górę, 2 lata w dół.

Wobec powyższego stworzymy 3 modele prognozy i wybierzemy najlepszy z nich. Specyfikacja w programie gretl.

1. AR(2) dla zmian proc. WIG. Tylko rzędu 2-go:

2. Sama regresja ze zmienną objaśniającą w postaci zmian proc. PKB UE(+1), tj. PKB przyspieszony o rok (model ARMAX(0, 0, GDP_UE(+1)):

3. Połączenie modelu (1) z (2): AR(2) + regresor w postaci zmian PKB UE(+1); AR tylko rzędu 2-go (model ARMAX(2, 0, GDP_UE(+1)):

Uwaga: Nie użyłem bezpośrednio obserwacji GDP_UE(+1) tylko posłużyłem się opóźnionym o rok WIG.

Jak widać wszystkie kryteria: AIC, BIC i HQC jednoznacznie wskazują, że model nr 3 jest najlepszy. Graficznie, model dobrze się jak dotąd spisywał:

Rok 2018 będzie raczej na giełdzie spadkowylub neutralny ze względu na zakończenie cyklu WIG (zob. Prognoza WIG dwiema metodami ), natomiast jeszcze pozostała kwestia kierunku PKB UE. Najłatwiej i najszybciej posłużyć filtrem Hodricka-Prescotta. Zgodnie z opisaną formułą w artykule Filtr Hodricka-Prescotta dla rocznych danych należy przyjąć lambdę na poziomie 6,25. W gretlu jedynie można wstawiać liczby całkowite, tzn. że lambda = 6. Uzyskałem w ten sposób nieliniowy trend gospodarki europejskiej:

Pamiętajmy, że ostatni rok to 2016, należy więc odpowiednio zrobić korektę dla 2017. Później pokażę prognozę z tą korektą.

W każdym razie składnik cykliczny bezwzględnie sygnalizuje, że wchodzimy w fazę stagnacji w UE. Trzeba przy tym pamiętać, że będzie to stagnacja wokół trendu rosnącego, tj. długoterminowej ekspansji.
Możemy nawet precyzyjnie przewidzieć zmiany składnika cyklicznego H-P. Za pomocą dodatku armax sprawdzamy najlepiej dopasowaną liczbę parametrów ARMA(p, q) modelu. Armax dał nam pewną zagwozdkę, bo AIC i HQC wybrały ARMA(0, 4), czyli czysty model średniej ruchomej 4-okresowej, natomiast BIC wybrał ARMA(2, 1). Chociaż najlepiej lubię posługiwać się HQC, bo jest swego rodzaju balansem między AIC a BIC (jego formuła to właśnie coś pomiędzy AIC i BIC), to ogólnie rzecz biorąc, gdy mamy do czynienia z niewielką liczbą danych albo procesem bardzo skomplikowanym (w tym sensie, że liczba parametrów prawdziwego modelu przekracza długość próby), to powinniśmy posługiwać się zawsze AIC. Z kolei BIC jest lepszy wtedy, gdy proces nie jest tak skomplikowany i wiemy z góry, że liczba parametrów prawdziwego modelu jest mniejsza od długości próby - zob. [1]. A w tym przypadku dodatkowo AIC pokrywa się z HQC. Nie ma wątpliwości: wybieramy model ARMA(0,4). Uzyskujemy prognozę:

W przypadku ostatniej analizy polskiego PKB ( zob. Prognoza PKB na 2018 czterema metodami ) prognoza była negatywna. Omawiana sytuacja sugeruje stabilizację, neutralność na bieżący rok i kontrakcję na kolejne lata.

----------------------------------------------------------------------------------
Zwiększenie jakości prognozy:
Jakość prognozy może zostać zmaksymalizowana dzięki uwzględnieniu najnowszych danych. Rok 2017 już za nami i można z dużą pewnością podać PKB na ten rok. Niedawno, w styczniu 2018 Bank Światowy zaktualizował prognozę różnych regionów na świecie [2]:

Podane stopy to "aggregate growth rates calculated using constant 2010 U.S. dollar GDP weights", tj. realne stopy wzrostu w dolarach amerykańskich, czyli te same miary, których dotychczas używałem. UE będziemy aproksymować poprzez strefę Euro.*

Zwróćmy uwagę, że Bank przewiduje osłabienie wzrostu gosp strefy euro w kolejnych latach. Do tego pesymistycznego wniosku sami dotarlibyśmy stosując filtr H-P. Poniższy wykres składnika cyklicznego tego filtru uwzględnia rok 2017:

Podsumowanie: Mimo iż WIG nie koreluje silnie z bieżącym PKB, to okazuje się, że silnie korelować z przyszłością gospodarczą, wyprzedzając ją o 1 rok. Zbudowany model prognozuje spadek WIG na 2018-2019.


* Poniższa grafika (która pochodzi z [3]) ilustruje, że strefa Euro praktycznie niczym się nie różni od UE:

Literatura:
[1]  Aho, K., Derryberry, D., Peterson, T., Model selection for ecologists: the worldviews of AIC and BIC, March 2014;
[2] https://data.worldbank.org/data-catalog/global-economic-prospect;
[3] Eurostat, "GDP up by 0.6% in both the euro area and the EU28", 20/2018 - 30 January 2018, http://ec.europa.eu/eurostat/news/news-releases

WIG dyskontuje prędzej Zagranicę niż Polskę

Dla zwykłego inwestora Skorygowany narodowy dochód netto (Adjusted net national income, ANNI), opisany ostatnio, jest co najwyżej tylko ciekawostką. Podaje się go z dużym opóźnieniem w stosunku do PKB i mniejszą częstotliwością. Mimo wszystko jego "czystość" może doprowadzić do ciekawych konkluzji. Zrobimy takie porównanie na trzy: między WIG, PKB, ANNI. Analizując te same roczne dane co poprzednio (1996-2015, 20 obs), przestudiujmy krótko w Gretlu wzajemne korelacje seryjne:

a) między tempem PKB Polski a różnymi opóźnieniami tempa WIG (korelogram wzajemny)

Liczbowo:

Co tu widzimy?
1) WIG już rok wcześniej przewiduje z siłą 0,6 jak zmieni się PKB i podąża w tym kierunku. Np. w 2008 r. spadł, bo przewidywał spadek wzrostu PKB w 2009 r. (istotnie wzrost gosp. spadł). Jest to zachowanie oczywiście zgodne z teorią efektywnego rynku.
2) Występują także inne korelacje w czasie, które zamazują ten obraz. Na przykład istnieje bardzo słaba korelacja PKB danego roku i WIG z tego samego roku (0,17). Nie jest jasne czy ta korelacja w ogóle jest prawdziwa. Dodatkowo pojawiają się też dość silne korelacje dalekich rzędów.

Poniżej dla porównania grafika relacji opóźnionego o 1 rok WIG z PKB:

 
Widać, że WIG przewiduje co się stanie z PKB już rok naprzód. A dodatkowo przecież dane o gospodarce udostępniane są z dużym opóźnieniem. Powoduje to, że znacznie trudniej jest przewidywać giełdę niż to sugerują analitycy, którzy dodają nawet wykresy tego "dowodzące". Co chwilę czytamy artykuły czy to na blogach czy serwisach, że WIG naśladuje krajową gospodarkę. Okazuje się to fałszem: jest wręcz na odwrót (dla jasności: chociaż to badanie jest tylko z lat 1996-2015, to dla lat 1995-2016 korelacja zmian WIG z PKB jest jeszcze mniejsza i wynosi zaledwie 0,128, a opóźnionego o 1 rok 0,4).

b) między tempem ANNI Polski a różnymi opóźnieniami tempa WIG

Liczbowo:

Z tej perspektywy obraz jest klarowniejszy. Indeks przewiduje zmiany ANNI 1-2 lata do przodu, a jednocześnie korelacje wsteczne (tzn. z ujemnymi opóźnieniami) są dużo słabsze. Ponadto nie występuje już żadna korelacja między PKB a indeksem okresu bieżącego. (Najprawdopodobniej wynika to z tego, że na ANNI ma miejsce silniejsza autokorelacja 1 rzędu niż PKB (0,51 vs. 0,36) właśnie dzięki temu, że jest oczyszczony z amortyzacji).
Ponieważ ANNI zawiera realne dochody ludności, to znaczy że zmiany WIG nie odzwierciedlają zmian dochodów z danego okresu, a jedynie przewidują przyszłe dochody. Tak więc tempo wzrostu polskiego PKB na 2018 nie będzie miało większego wpływu na giełdę w tym samym roku. 

Poniżej dla porównania grafika relacji opóźnionego o 1 rok WIG z ANNI:

Nieco gorsza korelacja ANNI niż w przypadku PKB wynika z tego, że ANNI Polski silniej naśladuje ANNI UE z rocznym opóźnieniem, a jednocześnie WIG także przewiduje ANNI UE rok naprzód (albo po prostu koreluje naprzód).


Powyższa analiza zakłada jednak, że pomiędzy PKB (lub ANNI) a WIG nie ma pośrednich zmiennych. Może być jednak tak, że PKB koreluje z pewnym opóźnieniem z gospodarkami zagranicznymi, a wtedy WIG przewiduje przyszłość gospodarczą poprzez naśladowanie koniunktury innych krajów. Porównajmy najpierw ze sobą takie kategorie jak WIG, PKB i ANNI dla Polski, UE i USA, tworząc macierz korelacji. Oto wyniki:

Rzeczywiście obraz się zmienia. Korelacja między bieżącymi WIG a ANNI_UE równa się 0,27. Co więcej jest znacznie większa niż między WIG a GDP_UE (0,19). Sprawdźmy teraz dokładniej te zmienne na korelogramie wzajemnym:

a) między tempem PKB UE a różnymi opóźnieniami tempa WIG

Wynik ten wskazywałby, że WIG koreluje słabo z bieżącym PKB UE, ale za to przewiduje co będzie rok później, silnie korelując z przyszłością gosp (0,51).

b)  między tempem ANNI UE a różnymi opóźnieniami tempa WIG

Przy niewielkiej liczbie danych korelacja jest nieistotna stat, ale widać, że dla opóźnienia = 0 i 1 jakaś występuje. ANNI dowodzi, że WIG koreluje z gospodarką europejską na bieżąco. Natomiast korelacja z przyszłym 1-szym okresem gospodarczym jest prawdopodobnie spowodowana faktem, że ANNI posiada autokorelacje 1 rzędu i tak naprawdę WIG raczej nie przewiduje przyszłości UE albo robi to w niewielkim stopniu.*
  
c) W takim razie sprawdźmy korelację między ANNI Polski na tle opóźnień ANNI UE:

I rzeczywiście polska gospodarka jest opóźniona w stosunku do UE o 1 rok, to znaczy reaguje z rocznym opóźnieniem, co potwierdza nasze sugestie co do WIG. Ewidentnie 0,27 jest nieprzypadkowo zbliżona do tej, którą zarejestrowaliśmy dla WIG-ANNI_UE, ale przesunięta o 1 okres do tyłu. 

Pomijam w tej analizie USA, żeby zachować jakąś przejrzystość, ale ogólnie wyniki są podobne, przy czym WIG nie reaguje na bieżącą koniunkturę USA, ale także wyprzedza ją o 1 rok.

Ok, to teraz najważniejszy element z całej tej układanki. Gdyby nie to, to cała analiza byłaby tylko ciekawostką bez większego znaczenia. Popatrzmy na:

d) relację między PKB Polski a PKB UE (na tle opóźnień PKB UE):

Zgodnie z tym schematem PKB Polski i UE koreluje z siłą 0,4, a dodatkowo PKB Polski reaguje z 1-rocznym opóźnieniem na to, co się dzieje w UE. Ale przecież zgodnie z ANNI korelacja gospodarek polskiej i UE o zerowym rzędzie opóźnienia praktycznie nie istnieje albo jest bardzo mała (0,13). A skoro wiemy, że ANNI jest bardziej obiektywne, to znaczy, że bieżące zmiany gospodarcze Polski nie odzwierciedlają bieżących zmian UE, tylko z opóźnieniem o 1 rok, natomiast to co pokazuje wzajemna korelacja PKB w pewnym sensie fałszuje rzeczywistość.
Dlatego właśnie WIG szybciej reaguje - po prostu patrzy na UE.

Wniosek końcowy: jeśli decydujemy się na inwestowanie aktywne, powinniśmy bardziej skupiać się zmianach w gospodarce europejskiej (i USA) niż polskiej. Nie znaczy to, że w ogóle należy pomijać Polskę, ale powinna ona stać na drugim planie, bo w dużej mierze reaguje z rocznym opóźnieniem na sygnały z zagranicy.


DODATEK:
* Tezę tę sprawdziłem. Ułożyłem dla zmiennej zależnej ANNI_UE model AR(1) wraz z opóźnioną stopą zwrotu o 1 rok WIG. Dostałem takie wyniki:

Wig opóźniony o 1, tj. wig_1 nie jest istotny. Po opuszczeniu tej zmiennej model się poprawił.
Sugeruje to, że WIG raczej nie przewiduje przyszłości ANNI_UE, który koreluje sam ze sobą. Przy okazji rysuje się pytanie czy model poprawi się gdy użyjemy nieopóźnionego WIG? Powinno tak być. Wyniki tego testu:

Mimo braku istotności, wszystkie kryteria (Akaike - AIC, Bayesa-Schwarza - BIC, Hannana-Quinna - HQC)  poprawiły się. A przecież korelacja pomiędzy (bieżącym) WIG a (bieżącym) ANNI była mniejsza niż pomiędzy opóźnionym WIG a (bieżącym) ANNI (0,27 vs 0,35). Mimo to, taki model jest lepszy, tzn. WIG reaguje bardziej na bieżącą koniunkturę UE.