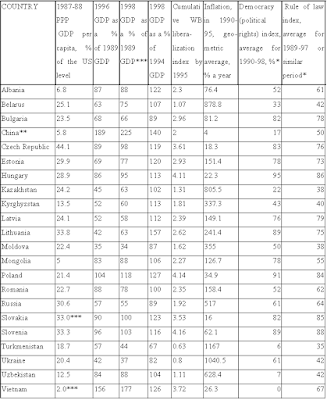
Wskaźnik ten wydaje się być podany jako niewyrównany sezonowo, co nawet GUS zaznacza w tabeli. Ale zarówno w "Uwagach ogólnych" jak i "Wyjaśnieniach metodycznych" GUS stwierdza, że dane dotyczące wskaźnika koniunktury zostały wyrównane sezonowo metodą TRAMO/SEATS. Skąd taka niekonsekwencja? Nie wiem. Powinny być to dane niewyrównane, bo występuje ewidentna cykliczność. Np. gdy powiększymy ten wykres dla lat 2014-2017 to zobaczymy idealnie ten sam wzór:
Obecnie mamy do czynienia ze szczytem cyklu, tzn. że trzeba spodziewać się pogorszenia nastrojów koniunkturalnych. Czy to oznacza, że giełda powinna reagować spadkiem? Oczywiście nie, bo efektywny rynek powinien dyskontować takie informacje o sezonowości, a więc racjonalny inwestor użyje narzędzia do wyrównania sezonowego.
Są dwie znane metody do tego: pierwsza to X-12-ARIMA, która niedawno została zastąpiona przez X-13-ARIMA-SEATS, a druga to TRAMO/SEATS. Obydwie bardzo łatwo użyć w Gretlu. Tutaj wyjaśniam skąd takie nazwy i co te programy robią, a także pokazuję jak wyciągnąć z nich prognozy.
Nie chcę się skupiać na teoretycznych aspektach tych metod, przejdę więc od razu do rzeczy, czyli do praktycznego zastosowania obydwu metod. Pakiety X-13-ARIMA i TRAMO/SEATS nie są automatycznie instalowane razem z Gretlem, dlatego musimy na stronie Gretla je najpierw ściągnąć i zainstalować, co nie jest żadnym problemem, bo po instalacji powinniśmy mieć te pakiety w Gretlu. Czasami mogą wystąpić problemy ze znalezieniem ścieżki. Żeby sprawdzić czy Gretl poprawnie łączy się z programem, wchodzimy w gretlu w: Narzędzia -> Ustawienia -> Ogólne -> Programy. Wyszukujemy tutaj "Ścieżka do programu X-12-ARIMA" (przynajmniej u mnie tak jest, że nie zaktualizowano nazwy na X-13-ARIMA) i "Ścieżka do programu TRAMO". Jeśli wyświetlona obok ścieżka jest błędna, to musimy ją poprawić.
Aby użyć metody, musimy mieć zaznaczoną naszą zmienną w oknie gretla,a sama zmienna musi być szeregiem czasowym o określonej wcześniej częstości, tutaj 12 miesięcy (jednak nie każda częstość jest dozwolona). Same programy działają po wejściu w Zmienna -> Analiza ... i w zależności od typu wybieramy program.
X-13-ARIMA-SEATS:
Przy standardowych opcjach, klikamy OK; wówczas GUS-owski Wskaźnik koniunktury budownictwa zostanie podzielony na 3 części: wyrównany sezonowo, trend/cykl oraz odchylenia przypadkowe:
Wyrównanie sezonowe nie jest filtrowaniem z odchyleń przypadkowych, a jedynie ze zmian sezonowych. Mówiąc prosto: zmienna 'wyrównany sezonowo' to zmienna złożona z dwóch części: 'trendu' oraz zmian przypadkowych.
Wynika z tego, że filtrowanie z danych sezonowych oraz ze zmian przypadkowych zawiera trend. Dlatego inwestor będzie najbardziej zainteresowany drugim wykresem, który wskazuje w jakiej fazie cyklu koniunkturalnego rzeczywiście się znajdujemy.
Oprócz wykresu dostajemy także bardzo duży zestaw statystyk, których ilość może zniechęcać do ich analizy. Ogólnie to interesuje nas tylko wybór modelu, jego parametry i istotność statystyczna. W zestawie otrzymanych danych szukamy terminu "Final automatic model choice". W tym przypadku dostajemy coś takiego:
Final automatic model choice : (0 1 1)(0 1 1)
Co oznacza, po kolei w 1 nawiasie:
AR(0) - czyli nie występuje autoregresja liniowa w oryginalnych danych (z miesiąca na miesiąc)
d = 1 - czyli oryginalne dane są niestacjonarne i trzeba je zamienić na zmiany pierwszego rzędu
MA(1) - występuje średnia ruchoma pierwszego rzędu (z miesiąca na miesiąc) w oryginalnych danych.
W 2 nawiasie:
SAR(0) - nie występuje sezonowa autoregresja
Sd = 1 - oryginalne dane są niestacjonarne i trzeba je zamienić na zmiany 12-miesięczne
SMA(1) - występuje sezonowa średnia ruchoma pierwszego rzędu w oryginalnych danych (nie mylić z Simple Moving Average z AT)
Trzeba pamiętać, że AR i MA odnoszą się do zmian z okresu na okres (tutaj z miesiąca na miesiąc). Natomiast SAR i SMA odnoszą się do zmian danego miesiąca w stosunku do zmian tego samego miesiąca z poprzedniego roku.
Istotność statystyczną sezonowości oceniamy szukając wyników do 3 testów:
- test na stabilność sezonowości: Test for the presence of seasonality assuming stability
Wynik:
Seasonality present at the 0.1 per cent level.
tj. sezonowość występuje poziomie istotności 0,1%.
- nieparametryczny test na stabilność sezonowości:Nonparametric Test for the Presence of Seasonality Assuming Stability.
Wynik:
Seasonality present at the one percent level.
- test na zmienność amplitudy sezonowości: Test na Moving Seasonality Test
Wynik:
Moving seasonality present at the one percent level
tj. wykryta sezonowość zmienia swoją wielkość (amplitudę) z okresu na okres przy 1% istotności.
Ta własność nie występowałaby gdyby np. w danym miesiącu zmiana byłaby zawsze taka sama.
Jak powiedziałem inwestor jest zainteresowany głównie trendem, a więc także jego prognozą. Jeżeli na początku zaznaczymy opcję 'Zapisywanie danych' - składnik trendowy, to możemy wykorzystać sam trend jako zmienną do prognozy. Jakie jednak przyjąć dla niej parametry? Skoro X-13-ARIMA poszukuje optymalnego modelu, to moglibyśmy ponownie wykonać całą procedurę już dla trendu - spodziewając się, że wskaże model bez sezonowości, np. (1, 1, 1)(0, 0, 0). Jak najbardziej jest to możliwe, jednak okazuje się, że gdy to zrobiłem, to dostałem:
Final automatic model choice : (3 2 1)(1 0 1) ,
co sugeruje, że sezonowość występuje także w trendzie!
Aby sprawdzić prognozę trendu, możemy wykorzystać zwykłą procedurę ARIMA (Model -> Modele szeregów czasowych -> model ARIMA) i zaznaczyć AR=3, d=2, MA=1, SAR=1, Sd=0, MA=1.
Wyniki:
Następnie sprawdzamy prognozę (Analiza -> Prognoza). Przy wyborze 12 miesięcy do przodu, można spodziewać się ożywienia w budownictwie:
Metoda ta ma ograniczenia w postaci maksymalnych rzędów części AR i MA. Jest też inna metoda. Instalujemy dodatek o nazwie armax (Narzędzia -> pakiety funkcji -> na serwerze gretla, tam wybieramy 'armax'). Dodatek ten jest fajny, bo szuka najlepszego możliwego modelu ARMAX (literka X oznacza tylko, że możemy dodać zmienną zewnętrzną do modelu) przy wybranym maksymalnym rzędzie AR i MA (nie ma tutaj ograniczeń). Ze względu na miesięczną częstotliwość, wybrałem max rząd 12 dla obydwu. I tu trzeba się zastanowić czy tak wysoki pułap chcemy sprawdzić, bo będziemy długo czekać zanim program przeliczy parametry AR i MA od 0 do 12. Jeśli zależy nam na tej liczbie, a chcemy przyspieszyć działanie, możemy zmienić metodę estymacji. Program używa dwóch metod: standardowa to dokładna metoda największej wiarogodności (exact ML), druga to metoda warunkowej wiarogodności (conditional ML).
Która metoda jest lepsza? Obydwa estymatory są zgodne, ale exact ML jest efektywniejsza od conditional ML w tym sensie, że jej wariancja jest najmniejsza [1], tzn. także lepsza od uogólnionej metody najmniejszych kwadratów - w sytuacji gdy występuje proces ARMA [2]. Ta druga jest jednak obliczeniowo bardzo szybka przy dużej liczbie parametrów.
Pamiętać należy o dwóch rzeczach: po pierwsze dodatek armax nie sprawdza sezonowości, co w naszym przypadku może być zaletą, bo już ją usunęliśmy; po drugie jeśli wiemy już, że nasz szereg jest niestacjonarną zmienną, to musimy przekształcić je w różnice (Dodawanie zmiennych -> pierwsze różnice), bo armax bada tylko model ARMAX, a nie ARIMAX.
Optimum zostaje osiągnięte, gdy kryteria AIC, BIC lub HQC osiągną najmniejszą wartość (tak jak entropia - im mniejsza, tym mniejsza niepewność co do modelu). Tutaj znów powstaje pytanie, które kryterium wybrać? Najczęściej wybierane jest AIC, jednak nie jest to wybór absolutny, co więcej nie jest optymalny w przypadku procesów ARMA. Hannan i Quinn [3] pokazali empirycznie, że ich kryterium, które potem zostało nazwane od ich nazwisk HQC, jest prawdopodobnie lepsze gdy proces jest autoregresyjny, a próba jest stosunkowo duża (np. powyżej 100). W przeciwnym wypadku AIC lub BIC może być lepsze. AIC minimalizuje błąd prognozy, a BIC razem z HQC dążą do wartości oczekiwanej prawdziwego modelu. Jeżeli wszystkie 3 kryteria wskazują najniższą wartość dla tego samego modelu, to nie mamy wątpliwości, że ten właśnie jest najlepszy z danego zestawu modeli. Dodatek armax umożliwia ocenę tych 3 kryteriów jednocześnie.
Najpierw użyłem metody exact ML, w której AIC, BIC i HQC wskazały jednoznacznie ten sam model: AR(4)-MA(2). Aby sprawdzić prognozę, robię to samo co poprzednio - używam standardowego modelu ARIMA, w której wpisuję odpowiednio rzędy parametrów (oczywiście bez sezonowości). Tym razem dostałem następujący wykres prognozy:
A więc zupełnie inna prognoza niż ta wzięta z X-13-ARIMA. Która jest bardziej prawdopodobna? Tutaj idealnie sprawdzą się kryteria AIC, BIC i HQC. Trzeba tylko wiedzieć, że:
AIC = Kryt. inform. Akaike'a
BIC = Kryt. bayes. Schwarza
HQC = Kryt. Hannana-Quinna
Zauważmy, że każdy z tych kryteriów jest niższy dla ostatniego modelu, co oznacza, że ożywienie w budownictwie nie jest wcale takie pewne.
Analogicznie sprawdźmy conditional ML. Wyniki tym razem nie są jednoznaczne, bo każde kryterium przynosi inne rezultaty. Biorąc pod uwagę, że mamy 199 obserwacji, wykorzystam wnioski Hannana i Quinna i skorzystam z HQC, które wskazało model AR(8)-MA(0). Użycie prognozy z tymi parametrami przyniosło bardzo podobną prognozę, co dla exact ML, tylko nieco bardziej stromą.
TRAMO/SEATS:
Drugą procedurą jest TRAMO/SEATS ("Time Series Regression with ARIMA Noise Missing Observations, and Outliers" / "Signal Extraction in ARIMA Time Series"). Przy standardowych opcjach, klikamy OK; GUS-owski Wskaźnik koniunktury budownictwa został podzielony na 3 części: wyrównany sezonowo, trend/cykl oraz odchylenia przypadkowe:
Znów dostaniemy skomplikowane statystyki, ale najbardziej interesuje nas to:
MODEL FITTED
NONSEASONAL P= 0 D= 1 Q= 1
SEASONAL BP= 0 BD= 1 BQ= 1
PERIODICITY MQ= 12
Przekładając na X13-ARIMA zapisalibyśmy to tak: (0, 1, 1)(0, 1, 1)
Czyli dostaliśmy ten sam schemat co w X-13-ARIMA. Nie zawsze jednak tak będzie.
Tutaj także możemy zapisać składnik trendowy (Wynik -> Zapisz...), który chcielibyśmy prognozować. Aby to zrobić możemy wybrać - tak jak poprzednio - jedną z dwóch metod. A więc pierwsza to zaznaczenie zmiennej trendu i użycie dla niej TRAMO-SEATS. Otrzymamy statystyki, wśród których szukamy:
MODEL FITTED
NONSEASONAL P= 3 D= 1 Q= 1
PERIODICITY MQ= 12
Zniknęła sezonowość (SEASONAL), co świadczy, że jesteśmy na dobrej drodze. Uzyskane parametry wykorzystujemy do prognozy, a więc znów wchodzimy w Modele szeregów czasowych -> ARIMA. Tam wpisujemy te parametry AR=3, I=1, MA=1. Wyniki:
I prognoza:
W przeciwieństwie do X-13-ARIMA, Tramo sygnalizuje szczyt.
Druga metoda to identycznie jak przy X-13-ARIMA użycie dodatku armax. Tworzymy więc pierwsze przyrosty zmiennej trendu, zaznaczamy tę nową zmienną i możemy porównać dwie pod-metody: exact ML i conditional ML. Wyniki dla exact ML nie są jednoznaczne. AIC wskazuje AR(6)-MA(10), BIC i HQC - AR(1)-MA(4). W dodatku conditional ML prowadzi do jeszcze innych wniosków: dla AIC AR(12)-MA(1), BIC AR(3)-MA(1) i HQC AR(6)-MA(1). Idąc tropem HQC, exact ML i conditional ML przynoszą podobną prognozę. Poniżej wykres dla pierwszej z nich.
Ta prognoza współgra z tą, przeprowadzoną na Tramo. Sugeruje stabilność w branży budowniczej, ale nie ożywienie. W sumie więc zaprzecza początkowej intuicji, że trend jest rosnący.
Uwaga na fałszywe trendy
Niedawno opisywałem filtr Hodrika-Prescotta. Przestrzegałem, że może być mylący, bo zawsze wskaże "trend" nawet, jeśli jest to tylko przypadek. Tutaj jest podobnie. Samą zmienną trendu nie można się sugerować. Może wspomagać, ale musi być powiązana z istotnością statystyczną modelowania pierwotnej zmiennej. Np. wygenerujmy 199 obserwacji procesu Browna i zastosujmy X-13-ARIMA. Dostaniemy:
Jaki otrzymałem model optymalny?
Final automatic model choice : (0 1 1)
Wprawdzie nie pokazał żadnej sezonowości, ale przecież powinniśmy mieć (0 1 0). Przekonamy się o tym dopiero gdy sprawdzimy istotność statystyczną takiego modelu; wtedy otrzymamy p = 0,63.
Tylko że ta wartość p dotyczy zmiennej ruchu Browna, a nie zmiennej "trendu". Ponieważ procedura filtruje dane, to zaczyna tworzyć sztuczny trend.
Dlatego nie można się sugerować tutaj nazwą "trend", bo prawidłowo powinno brzmieć po prostu "filtr". Dlatego zarówno X-13-ARIMA jak i TRAMO/SEATS wymagają dużej ostrożności przy wnioskowaniu co do przyszłości.
Literatura:
[1] Andersen, E. B., Asymptotic Properties of Conditional Maximum-Likelihood Estimators, 1970,[2] Beach, C. M., MacKinnon, J. G., A Maximum Likelihood Procedure for Regression with Autocorrelated Errors, Jan. 1978,
[3] Hannan, E. J., Quinn, B. G., The Determination of the Order of an Autoregression, 1979.
P. S. Więcej informacji na temat tych programów (m.in. ich historii) napisałem tutaj.