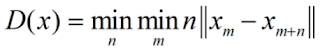Wpis chwilowy - "eksperci" nagle zdziwieni skalą inflacji

Kolejne rekordy inflacji "szokują". Jak żenujące są słowa tzw. ekspertów, którzy twierdzą, że nie dało się przewidzieć skali wzrostu cen. Za co oni biorą pieniądze? To ja zrobiłem darmowe analizy, które przewidywały, że do tego dojdzie, którymi nikt jak widać się nie zainteresował. Już w 2020 r. wskazałem na ryzyko 20% inflacji, najpierw na skutek zablokowania podaży towarów: Czy powinniśmy przygotować się na inflację rzędu 20%?, potem wskazałem na niebezpieczeństwo zbyt niskiej stopy (Inflacja a luka PKB) i w końcu ostrzegałem przed tym scenariuszem, który już praktycznie ma miejsce, a który wówczas wydawał się absurdalny: Widmo 20-procentowej inflacji powraca. I co, i dziś okazuje się, że inflacja PPI skoczyła w grudniu do 14,2%.  Brak realnej odpowiedzialności za sytuację dowodzi, że należy albo ograniczyć rolę NBP w niektórych obszarach, albo wprowadzić sankcje personalne, bo nie może być tak, że prezesi i ich doradcy biorą grube pieniądze za bezmyślne naśladowanie innych krajów (bo do tego nie są potrzebne żadne kwalifikacje) albo za zaklinanie rzeczywistości i udawanie, że w ogóle coś się robi.

Zniesienia Fibonacciego mogą być optymalne

Na swojej stronie znany wielu trader T. Bulkowski napisał, że zniesienia Fibonacciego przestały działać. Dokładniej przekierowuje czytelnika tutaj, gdzie czytamy: "I found that the three Fibonacci retrace values of 38%, 50%, and 62% were no more likely to appear than any other number from 1% to 100%." Należy dodać, że jego statystyki dotyczą wyłącznie giełdy w USA. I oczywiście nie można się było  spodziewać, że Fibo będą działać zgodnie z jakimś schematem, np. dominanta skumuluje się wokół wartości 38% i/lub 62%. Wręcz przeciwnie, należało się właśnie spodziewać, że nie będzie to działać w ten sposób, bo byłoby to za proste. Jeżeli przed 2009 r. taka technika działała, a po 2009 przestała, to zgodnie z teorią efektywnego rynku inwestorzy zaczęli ją maksymalnie wykorzystywać.

Mimo to okazuje się, że zastosowanie złotego podziału nie jest metodą ad-hoc czy rodzajem voodoo, jak by niektórzy chcieli. Należy ją traktować jako sposób optymalizacji poziomu stopy zwrotu przy danym horyzoncie czasu lub optymalizacji czasu trzymania ryzykownych aktywów przy założonej stopie zwrotu. Kiedyś już napisałem krótki artykuł o znaczeniu złotego podziału w przyrodzie i na rynkach - zob. O fraktalnej naturze liczby Phi. Dlaczego liczba ta jest lepsza niż inne? , jednak kontekst ograniczał się wtedy do znaczenia fraktalności Phi. 

Weźmy okrąg o obwodzie równym 1. Na obwodzie tym zaznaczamy sekwencję liczb od 0 do 1, którą oznaczymy x = (x1, x2, ...). Chung i Graham [1] dowiedli, że odchylenie 

(1)

gdzie n oraz m są większe lub równe 1, oraz

posiada maksimum w punkcie 0,381966011..., tzn. 

Zauważmy, że:

Najpierw jest minimalizowany iloczyn n i odległości między dwoma punktami na okręgu. Im większe n, to iloczyn rośnie, ale z drugiej strony liczba podziałów na okręgu też rośnie, a więc owa odległość jednego punktu od drugiego musi maleć. Jeżeli n utożsamimy ze zmienną czasu, to wspomniany iloczyn interpretować możemy jako średnią zmianę ceny w jednostce czasu (np. 1 dzień) przemnożoną przez określoną liczbę dni. Taką wielkość najpierw minimalizujemy, aby działać w jak najkrótszym horyzoncie czasowym. Ale to ciągle funkcja, a nie konkretna liczba. Dopiero w tym czasie poszukiwane jest maksimum, które wynosi 0,382.

Z kolei Glover et al. [2] pokazali dokładnie to, czego szukamy - że użycie zniesienia Fibonacciego 62% jest optymalne dla ruchu Browna. Właściwie chodzi o część radialną trójwymiarowego ruchu Browna, czyli przypomina to trochę to wcześniejsze twierdzenie na okręgu, z zaprzęgniętym dodatkowo procesem stochastycznym. Poza tym poprzednie twierdzenie dawało liczbę 0,38, podczas gdy teraz mowa o 0,62. Powiedzmy, że mamy całkowity ruch, który liczymy jako 100%. Teraz następuje zniesienie 62% ruchu - zostaje 38%. To nasza lokalna stopa zwrotu. Dlaczego rozumiemy ją jako optimum? Kluczowym założeniem jest to, co się dalej dzieje z aktywem. W przypadku zniesienia mamy założenie, że cena po wystąpieniu bańki będzie spadać do zera. Chociaż można by spojrzeć na to z perspektywy cyklu życia firmy / produktu, to w praktyce spekulacyjnej zamiast pełnej wartości bierze się raczej lokalne "cykle", w których teoretyczne zero stanowią lokalne dołki lub górki (w zależności od kierunku zniesienia). W pracy można też znaleźć nawiązanie do rozszerzenia (zasięgu) Fibonacciego, 162%. Autorzy wskazują możliwość wykorzystania go do sprzedaży aktywów podczas bańki spekulacyjnej. W tym przypadku założenie jest odwrotne - cena będzie rosnąć do nieskończoności. Ponieważ to założenie jest naturalne dla wielu instrumentów, to Fibo można wykorzystać w tym przypadku na dwa sposoby: w odniesieniu do lokalnych cykli (wtedy punkt zero jest bardzo umowny - można ustawić na dowolnie lokalnym dołku lub górce, niekoniecznie ostatnich) oraz do samej ceny (wtedy jednak cel ustalamy aż na 162% bieżącej ceny - szczyt bańki). Na pewno jest to temat jeszcze do przestudiowania, ale trzeba przyznać, że uzyskanie takiego rozwiązania jest niesamowite.

Literatura:

[1] Chung, F., Graham, R. On the discrepancy of circular sequences of reals, 2016;

[2] Glover, K., Hulley, H., Peskir, G.  Three-dimensional Brownian motion and the golden Ratio Rule, 2013.