Gdy nie znamy rzeczywistej oczekiwanej stopy zwrotu oraz stopy zwrotu posiadają rozkład zbliżony do normalnego, ale bez autokorelacji, wtedy możemy zastosować formułę Blume'a:
(1)
gdzie:
M^N - skumulowana długookresowa oczekiwana stopa zwrotu
T - okres przeszłości dla danych historycznych
N - okres przyszłości (horyzont inwestycyjny)
A - średnia arytmetyczna stopa brutto (liczona dla danych z okresu T)
G - średnia geometryczna stopa brutto (liczona dla danych z okresu T)
Jeżeli jednak stopy zwrotu posiadają rozkład log-normalny i także nie zawierają autokorelacji, wtedy powinniśmy użyć formuły Jacqiuera-Kane'a-Marcusa (JKM):
(2)
(3)
JKM podali także wzór w sytuacji, gdy dodatkowo występują autokorelacje [1]. Ponieważ w tej analizie mamy podział na dwa okresy: przeszłości (T) oraz przyszłości (N), to także autokorelacja formalnie powinna zostać podzielona na takie części. Ponadto jest jeszcze jedna kwestia komplikująca analizę: autokorelację zazwyczaj rozumiemy jako autokorelację pierwszego rzędu, ale ogólnie może być też drugiego, trzeciego itd. Powoduje to, że autokorelacja staje się wektorem a w zapisie macierzowym - macierzą. Taką notację na macierzach stosują JKM.
Macierz autokorelacji 1-go rzędu wygląda następująco:
(4)
gdzie a(1) to współczynnik autokorelacji 1-go rzędu.
Macierz autokorelacji T-go rzędu wygląda więc następująco:
(5)
Jedynki na głównej przekątnej są oczywiście wynikiem tego, że niektóre wiersze i kolumny mają ten sam numer, więc stopa zwrotu koreluje sama ze sobą.
Macierz C(T) przekształci się w liczbę, gdy przemnożymy ją z lewej strony przez wektor jednostkowy transponowany (oznaczony I "prim"), a z prawej przez wektor jednostkowy:
(6)
Gdy wszystkie współczynniki autokorelacji są równe 0, liczba z (6) będzie równa T.
Analogicznie sytuacja będzie wyglądać dla autokorelacji w przyszłości, czyli dla N: literka T zostaje zamieniona na N we wzorach (4)-(6).
JKM stosują następujący wzór:
(7)
który można zapisać w skrócie:
(8)
gdzie:
F(T) = I(T)' C(T) I(T) / T
F(N) = I(N)' C(N) I(N) / N
Zróbmy teraz 4 teoretyczne przykłady. We wszystkich T = 4 i N = 3.
1) Dla C(T) współczynnik autokorelacji 1-rzędu wynosi -0.4, a pozostałe 0. Oznacza to, że stopa zwrotu 0-wego rzędu będzie korelować ze stopą zwrotu 1-go rzędu tak samo jak 2-go rzędu z 1-m rzędem oraz 3-go z 2-m rzędem. Stąd:
Teraz obliczmy F(T) i F(N):
F(T) = 1,6 / 4 = 0,4
F(N) = 1,4 / 3 = 0,47
Uzyskujemy F(T)/F(N) = 0.86.
2) Dla C(T) współczynnik autokorelacji 1-rzędu wynosi -0.6. Otrzymamy:
Dla C(N) współczynnik autokorelacji 1-rzędu nie zmieni się. Dostaniemy:
Obliczmy F(T) i F(N):
F(T) = 0,4 / 4 = 0,1
F(N) = 0,6 / 3 = 0,2
Uzyskujemy F(T)/F(N) = 0.5.
3) Dla C(T) współczynnik autokorelacji 1-rzędu wynosi 0.4. Otrzymamy:
Dla C(N) współczynnik autokorelacji 1-rzędu nie zmieni się. Dostaniemy:
Ponownie obliczmy F(T) i F(N):
F(T) = 6,4 / 4 = 1,6
F(N) = 4,6 / 3 = 1,53
Uzyskujemy F(T)/F(N) = 1,04.
4) Dla C(T) współczynnik autokorelacji 1-rzędu wynosi 0.6. Otrzymamy:
Dla C(N) współczynnik autokorelacji 1-rzędu nie zmieni się. Dostaniemy:
Tak jak poprzednio obliczamy F(T) i F(N):
F(T) = 7,6 / 4 = 1,9
F(N) = 4,6 / 3 = 1,8
Uzyskujemy F(T)/F(N) = 1,06.
Wniosek: Z dodatnią autokorelacją stosunek F(T) / F(N) > 1, natomiast w ujemną autokorelacją F(T) / F(N) < 1.
W artykule Jak prawidłowo obliczać procenty składane dla niepewnych aktywów? twierdziłem, że raczej nie powinniśmy używać N > T, bo prowadzi to nadmiernego obniżania oczekiwanej długookresowej stopy zwrotu. Jeżeli N < T, wówczas formuła (8) będzie prowadzić do ważnej konkluzji. Tej konkluzji jednak jeszcze nie widać z następującego powodu. Chociaż zazwyczaj średnia arytmetyczna jest większa niż geometryczna, to ze wzoru (2) i (7) tak nie wynika. W praktyce może się zdarzyć, że G > A. Jednak wzór (2) powstał jak pamiętamy z założenia, że rozkład stóp zwrotu jest log-normalny. W rozkładzie log-normalnym G zawsze jest mniejsza od A. W artykule W poszukiwaniu nieznanej wartości oczekiwanej - część 2 są podane następujące dwa wzory (oznaczone tam odpowiednio numerami 4 i 7):
gdzie
g - średnia geometryczna stopa kapitalizacji ciągłej w rozkładzie lognormalnym, wyznaczona z okresu od 1 do T,
σ^2 - wariancja logarytmicznej stopy (z okresu od 1 do T),
co jednoznacznie wskazuje, że G < A.
W ten sposób ujawnia się następująca konkluzja. Dopóki N < T:
- jeśli autokorelacja jest dodatnia, to obniża ona (długookresową) oczekiwaną stopę zwrotu (stosunek F(T) / F(N) > 1, zatem G będzie mieć wyższy udział, natomiast A niższy, a G jest mniejsza od A);
- jeśli autokorelacja jest ujemna, to podwyższa ona (długookresową) oczekiwaną stopę zwrotu (stosunek F(T) / F(N) < 1, zatem G będzie mieć niższy udział, natomiast A wyższy, a G jest mniejsza od A) .
Przykład nr 1. Miesięczne stopy zwrotu sWIG80 luty 2007 - czerwiec 2018 (T = 137).
Korelogram stóp zwrotu ujawnia bardzo wysoką dodatnią autokorelację rzędu 1 (0,38), a wg PACF także delikatnie ujemną rzędu 12-tego (tj. rok do roku, -0,23):
Należy zwrócić uwagę, że to PACF jest ważniejsze w analizie autokorelacji konkretnych rzędów. ACF pokazuje siłę i kierunek całej drogi od 12-tego rzędu do 0-wego rzędu, a PACF siłę i kierunek samego 12-tego rzędu w stosunku do 0-wego rzędu. W naszym przypadku ACF pokazuje, że pomiędzy dzisiejszą zmianą a zmianą 12-tego rzędu jest linia płaska, brak zależności. Natomiast PACF pokazuje, że dzisiejsza zmiana korelowała ujemnie ze zmianą 12-tego rzędu. Dlatego ACF lepiej nadaje się do badania niestacjonarności niż autokorelacji.
Z drugiej strony JKM stosują jedynie ACF i nie wspominają o PACF. Dlatego użyjemy tej samej co oni metody. Stąd, aby uzyskać wartości teoretyczne, zastąpiłem wszystkie współczynniki autokorelacji, za wyjątkiem rzędu 1, zerami.
Średnia geometryczna netto, g = -0,09% oraz brutto, G = 0,9991. Średnia arytmetyczna netto, a = +0,09% oraz brutto, A = 1,0009. Gdyby autokorelacje nie występowały, wtedy użylibyśmy wzoru (1) lub (2). Zakładamy lognormalność, czyli wybieramy (2). Dostalibyśmy wtedy dla:
* 1 roku naprzód, tj. N = 12, M^12 = 1,0089, czyli netto 0,89%,
* 2 lata naprzód, tj. N = 24, M^24 = 1,0141, czyli netto 1,41%,
* 3 lata naprzód, tj. N = 36, M^36 = 1,0155, czyli netto 1,55%,
* 4 lata naprzód, tj. N = 48, M^48 = 1,013, czyli netto 1,3%,
* 5 lat naprzód, tj. N = 60, M^60 = 1,0067, czyli netto 0,67%,
* 6 lat naprzód, tj. N = 72, M^72 = 0,9967, czyli netto -0,33%.
Dane te przeniosłem na wykres:
Zatem 3-letnia inwestycja przynosi najwyższy oczekiwany profit. Dzieje się tak dlatego, że na początku ujawnia się mechanizm kapitalizacji, czyli procentu składanego - zyski się kumulują. Jednak ta kumulacja staje się coraz wolniejsza na skutek niepewności, która daje o sobie znać tym silniej, im dłużej aktywa są wystawiane na ryzyko. W pewnym momencie skumulowana oczekiwana stopa zwrotu "nie wytrzymuje presji niepewności" i zaczyna spadać. Należy tu jednak dodać, że nie dzieje się tak zawsze. Istotna jest wielkość G. Im jest ona mniejsza w stosunku do A, tym szybciej nastąpi maksimum.
Teraz uwzględnimy autokorelację, czyli podstawiamy dane do (8). Obliczamy więc najpierw F(T) i F(N). Wiemy, że T = 137, więc:
F(137) = I(137)'*C(137)*I(137) / 137 = 1,73.
Następnie obliczamy to samo, ale dla kolejnych N:
* 1 roku naprzód, tj. N = 12, F(12) = 1,67. Zatem F(137) / F(12) = 1,033. M^12 = 1,0089, czyli netto 0,89%,
* 2 lata naprzód, tj. N = 24, F(24) = 1,706. Zatem F(137) / F(24) = 1,0148. M^24 = 1,014, czyli netto 1,4%,
* 3 lata naprzód, tj. N = 36, F(137) / F(36) = 1,009. M^36 = 1,0153, czyli netto 1,53%,
* 4 lata naprzód, tj. N = 48, F(137) / F(48) = 1,006. M^48 = 1,013, czyli netto 1,3%,
* 5 lat naprzód, tj. N = 60, F(137) / F(60) = 1,004. M^60 = 1,0065, czyli netto 0,65%.
* 6 lat naprzód, tj. N = 72, F(137) / F(72) = 1,003. M^60 = 0,9964, czyli netto -0,36%.
Autokorelacja minimalnie obniżyła oczekiwaną stopę zwrotu. Jest to różnica nieistotna, więc wykres dla autokorelacji będzie identyczny z tym bez autokorelacji. Nadal 3 lata inwestycji pozostaje optymalnym horyzontem inwestycyjnym.
Przykład nr 2. Roczne stopy zwrotu S&P 500, 1981-2017 (T = 37).
Korelogram stóp zwrotu ujawnia istotną ujemną autokorelację rzędu 5-tego, C = -0,42:
Pozostałe parametry to A = 1,094 (a = 9,4%) i G = 1,082 (g = 8,2%). Zakładając lognormalność stóp i brak autokorelacji, użylibyśmy wzoru (2) i dostalibyśmy dla:
* 1 roku naprzód, tj. N = 1, M^1 = 1,094, czyli netto 9,4%,
* 5 lat naprzód, tj. N = 5, M^5 = 1,555, czyli netto 55,5%,
* N = 6, M^6 = 1,7, czyli netto 70%,
* N = 10, M^10 = 2,38, czyli netto 138%,
* N = 15, M^15 = 3,6, czyli netto 260%,
* N = 20, M^20 = 5,35, czyli netto 435%,
* N = 25, M^25 = 7,84, czyli netto 684%,
* N = 30, M^30 = 11,32, czyli netto 1032%,
* N = 35, M^35 = 16,11, czyli netto 1511%.
Przypomnijmy, że T = 37, więc nie powinniśmy już zwiększać N.
W przeciwieństwie do poprzedniego przykładu, M^N nie osiąga tym razem maksimum. Średnia geometryczna okazuje się zbyt bliska arytmetycznej , aby tak się stało. Z tej perspektywy nie istnieje optymalny horyzont inwestycyjny.
Następnie uwzględnimy autokorelację, czyli podstawmy dane do (8). Aby uzyskać wartości teoretyczne w macierzy autokorelacji, zastąpiłem wszystkie współczynniki autokorelacji zerami - za wyjątkiem rzędu 5-tego.
Poszukujemy najpierw F(T), a potem F(N). Ponieważ T = 37, to uzyskałem:
F(37) = I(37)'*C(37)*I(37) / 37 = 0,27.
Dostaniemy wtedy dla:
* 1 roku naprzód, tj. N = 1, F(1) = 0,27. Zatem F(37) / F(1) = 1. M^1 = 1,094, czyli netto 9,4%,
* N = 5, F(5) = 0,27. Zatem F(37) / F(5) = 1. M^5 = 1,555, czyli netto 55,5%,
* N = 6, F(6) = 0,86. Zatem F(37) / F(6) = 0,313. M^6= 1,71, czyli netto 71%,
* N = 10, F(10) = 0,58. Zatem F(37) / F(10) = 0,465. M^10= 2,42, czyli netto 142%,
* N = 15, F(37) / F(15) = 0,62. M^15= 3,69, czyli netto 269%,
* N = 20, F(37) / F(20) = 0,734. M^20 = 5,53, czyli netto 453%,
* N = 25, F(37) / F(25) = 0,83. M^25 = 8,1, czyli netto 710%,
* N = 30, F(37) / F(30) = 0,91. M^30 = 11,6, czyli netto 1061%,
* N = 35, F(37) / F(35) = 0,98. M^35 = 16,23, czyli netto 1523%,
W tym przypadku autokorelacje nieco zwiększyły oczekiwane zyski, a największą różnicę dostajemy dla 30 lat (ok. 30 pkt proc.). Zauważalna różnica pojawia się dopiero dla 10-letniej inwestycji, dla której nadwyżka zwrotu wynosi 4 pkty proc. Z długiej perspektywy obydwie formuły dają podobny obraz, a przebieg obu scenariuszy ilustrują poniższe wykresy:
Uzyskany poprzednio "optymalny" horyzont inwestycyjny za pomocą CAPM (4 lata), nie powinien być w takiej sytuacji w ogóle brany pod uwagę, bo formalnie odpowiadał on na pytanie jaki musi być minimalny udział aktywów ryzykownych w portfelu przy danym horyzoncie inwestycyjnym. Zakłada się więc wtedy, że minimum udziału to jakby optimum udziału, a więc że towarzyszący mu horyzont także jest optymalny.
Pozostaje w takim razie pytanie dlaczego uzyskane "optymalne" horyzonty inwestycyjne (3-4 lata) są tak bardzo zbliżone do siebie w obydwu podejściach, chociaż obydwa są niezależne od siebie? Być może to przypadek, jednak trzeba przyznać, że w pewnym sensie zgodny rezultat staje się bardziej wiarygodny, a dwie różne metody wzmacniają się nawzajem. Czy to oznacza, że powinniśmy naprawdę trzymać akcje najwyżej 4 lata? Oczywiście że nie, przedstawiona analiza jest tylko pewną symulacją opartą na ostatnich 10 latach giełdy. Możemy traktować to jako punkt zaczepienia, gdy z góry chcemy ustalić okres inwestycji.
Wnioski końcowe:
Okazuje się, że jeśli inwestujemy długoterminowo, to lepiej szukać aktywów, które posiadają ujemną autokorelację stóp zwrotu. Jednak zauważalna różnica pojawia się dopiero dla długich horyzontów, np. ok. 10-letniej inwestycji (w przypadku S&P 500 dostaliśmy +4 pkty proc.). Dla 15-letniej nadwyżka to już ok. 10 pktów proc.
Odwrotnych efektów możemy się spodziewać dla walorów o dodatniej autokorelacji. Można by więc powiedzieć, że lepiej unikać takich walorów na długi okres. Jednakże jeśli inwestujemy w takie walory do 5 lat, to nie odczujemy negatywnych skutków, gdyż ujemny wpływ będzie zaniedbywalny.
Z tej perspektywy dobrym pomysłem jest ustalanie horyzontów inwestycyjnych. Jeśli nasze akcje zachowują się tak jak sWIG80, czyli posiadają dużą pozytywną autokorelację, to wydaje się dobrym pomysłem trzymanie ich nie dłużej niż 4-5 lat, bo po pierwsze ostatnia historia wskazuje, że to optimum, a po drugie później zaczynają coraz silniej oddziaływać ujemne efekty dodatniej autokorelacji. Jeśli z kolei nasze walory zachowują się tak jak S&P 500, czyli posiadają ujemną autokorelację któregoś rzędu, to 10 lat może okazać się minimum, aby otrzymać "nagrodę za cierpliwość".
Literatura:
[1] E. Jacqiuer, A. Kane, A. Marcus, Optimal Forecasts of Long-Term Returns and Asset Allocation: Geometric, Arithmetic, or Other Means?, October 31, 2002.
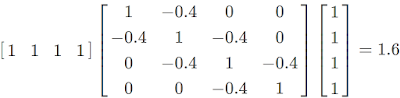
Brak komentarzy:
Prześlij komentarz