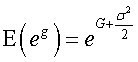Czy młodsze spółki mają większą stopę zwrotu?

Niewątpliwie inwestowanie w spółki, które stosunkowo niedawno pojawiły się na giełdzie, jest obarczone wyższym ryzykiem niż w spółki notowane od co najmniej paru lat. W dokumentach informacyjnych i prospektach emisyjnych nowe spółki prezentują często prognozy swoich wyników na następne lata. Takie dane mogą mieć różną wartość informacyjną, ale tak naprawdę największym ryzykiem dla inwestorów są zarządzający spółką ludzie: nie wiadomo czy można na nich polegać. Dopiero kolejne lata działalności spółki, ocena jej komunikatywności z rynkiem i zderzenie zapowiedzi z faktycznymi wynikami finansowymi, zmniejszają niepewność szacunków prognozowanych wyników.

Jednakże jak już wykazano w artykule Kiedy większa niepewność zwiększa wartość akcji? nie zawsze większe ryzyko oznacza, że inwestor może oczekiwać większych zwrotów. (pełne zwroty można uzyskać wykorzystując dywersyfikację ryzyka).

Pastor i Veronesi (PV) w [1] wyprowadzili model, w  którym rynek uczy się oceniać, czego może się po spółce spodziewać, stopniowo rozpoznając średnią ROE w czasie. W modelu wykazano, że oczekiwana stopa zwrotu z akcji jest niezależna od niepewności ROE. Ściślej, niepewność ROE została zdefiniowana jako wariancja warunkowa średniej w czasie (t) ROE i jest dana wzorem:

gdzie



- wariancja średniej ROE

 - szybkość powrotu ROE do średniej 

 - wariancja "niesystematyczna", tj. zmienność charakterystyczna dla danej spółki (zmienność "siły monopolistycznej", zmienność wyników ponadnormalnych).

Zauważmy, że niepewność ROE zależy tylko od jednej zmiennej w czasie: samego czasu (t). Wszystkie pozostałe składniki są to stałe. Wzrost t powoduje spadek niepewności, ponieważ rynek uczy się rozpoznawać średnią ROE. Należy się więc spodziewać, że w każdym kolejnym roku niepewność będzie spadać - oczywiście tak będzie tylko pod warunkiem, że "stałe" pozostaną stałe. Jednocześnie oczekiwana stopa zwrotu powinna pozostać na zbliżonym poziomie.

Przypomnijmy, że większa niepewność ROE podnosi wskaźnik P/BV. Ale teraz to oznacza, że im starsza spółka na giełdzie, tym P/BV powinien być niższy. PV zweryfikowali ten ciekawy wniosek empirycznie. Do badania użyli rocznych danych od 1962 do 2000 r. z CRSP/Compustat database. Poniżej widzimy w formie graficznej jak to twierdzenie spełniało się w rzeczywistości:

Rzeczywista zależność okazuje się zgodna z modelem PV. 

No i w końcu nasz ulubiony, czyli najbardziej skomplikowany temat - wzajemny związek z oczekiwaną stopą zwrotu. Mamy w modelu 2 zmienne objaśniające: oczekiwaną stopę zwrotu oraz zmienność średniej ROE (niepewność), i jedną zmienną objaśnianą: wskaźnik P/BV. Jak to zostało wcześniej dyskutowane, oczekiwana stopa zwrotu i niepewność ROE są nieskorelowane. Są to więc zmienne od siebie niezależne, czyli mogą niezależnie opisywać relację z P/BV. Większa oczekiwana stopa zwrotu zmniejsza P/BV. Pozornie to wydaje się oczywiste: większa stopa dyskontowa zmniejsza wartość akcji P, więc wskaźnik spada. Problem polega tylko na tym, że wycena kapitału własnego BV opiera się też na stopie dyskontowej: wartości poszczególnych składników majątkowych są obliczane na takiej samej zasadzie jak akcje (np. wycena nieruchomości metodą dochodową, czyli DCF). Wiadomo jednak, że księgowa aktualizacja wartości składnika majątkowego odbywa się nieporównywalnie rzadziej w stosunku do wartości rynkowej i na dodatek nie na zasadach rynkowych. Dlatego właśnie zmiana stopy dyskontowej będzie miała prawie zawsze tylko wpływ na licznik, czyli P. Stąd rzeczywiście powinniśmy zaobserwować ujemną korelację pomiędzy oczekiwaną stopą zwrotu a P/BV.

PV przetestowali hipotezę tej zależności empirycznie. Skoro P/BV spada w kolejnych okresach, to powinniśmy się spodziewać, że stopa zwrotu będzie rosnąć. Przybliżeniem dla oczekiwanej stopy zwrotu była więc stopa zwrotu w przyszłym roku. Należy tu zaznaczyć, że oczekiwana stopa zwrotu odnosi się do dziś, zaś sama stopa zwrotu do przyszłego okresu. Jeśli np. na koniec grudnia P/BV wynosi 2,25, to roczna stopa zwrotu w przyszłym roku wyniosła -2,7%. Na podstawie statystyk opracowanych przez PV we własnym zakresie przeprowadziłem graficzną zależność pomiędzy tymi dwiema zmiennymi (oś pozioma - AGE - to wiek uśrednionej w sensie pobytu na giełdzie):

Zaskakujące jest to, że średnie stopy zwrotu w początkowych latach są ujemne. To niewątpliwie zaprzecza tezie, że młodsza spółka powinna przynieść wyższą stopę zwrotu. Co ciekawe, relacja jest wręcz przeciwna: im młodsza spółka, tym mniejsza stopa zwrotu. Na rysunku tego nie widać, ale w rzeczywistości, w późniejszych latach życia, zarówno P/BV jak i stopa zwrotu się normują: stopa zwrotu będzie się zawierać w przedziale 9-11%, a P/BV trochę ponad 1 (księgowa wartość nie uwzględnia w pełni kapitału intelektualnego, a także synergii pomiędzy aktywami).

Zwróćmy jednak uwagę, że w takim razie istnieje empiryczna ujemna zależność pomiędzy niepewnością ROE a oczekiwaną stopą zwrotu: niepewność ROE spada wraz z czasem, a stopa zwrotu wzrasta. Jest więc możliwe, że omawiana ostatnio zagadkowa ujemna zależność pomiędzy niepewnością wyników finansowych a średnią stopą zwrotu została właśnie wyjaśniona. Trzeba jednak pamiętać, że w długim okresie ta zależność zanika, gdyż niepewność staje się minimalna, a zmiany w stopach zwrotu zależą od zupełnie innych czynników. Stąd ogólnie, ich wzajemna zależność nie występuje, choć w początkowych okresach jest taka możliwość (przynajmniej empirycznie).

Na koniec warto się zastanowić, jak te zależności prezentują się na polskiej giełdzie? Dobrze byłoby porównać młody rynek, jakim jest NewConnect ze starszym WIG20. Poniżej P/BV i roczne przyszłe stopy zwrotu dla NewConnect od końca grudnia 2007 do 7.12.2012:

P/BV zgodnie z modelem jest początkowo wysoki i spada w czasie. Ujemna zależność ze stopą zwrotu wydaje się bardzo słaba, ale jednak korelacja liniowa wynosi -0,75. Możemy spróbować zrobić uproszczoną prognozę stopy zwrotu w przyszłym okresie w oparciu o poprzedni P/BV. Otrzymałem następujące oceny parametrów regresji liniowej:

 Model         0.074    -0.0198*P/BV(NC)
 St. Error     (6.025)   (14.49)

R^2adj. = 40.7%,  R^2 = 55.6% 

Dopasowanie prognozy stopy zwrotu (linia zielona) do faktycznej stopy zwrotu (linia niebieska) jest następujące:

Jeśli potraktować wiarygodnie taki model, to jeśli pod koniec grudnia P/BV wyniesie tyle co na dzień dzisiejszy, czyli 1,9, to moglibyśmy się spodziewać stopy zwrotu 3,64% w 2013 r.

Następnie to samo dla WIG20 też od końca grudnia 2007 do 7.12.2012:

Ujemna korelacja okazuje się wręcz idealna. Korelacja liniowa wynosi -0,885 i jest istotna. Regresja liniowa, gdzie zmienną objaśnianą jest stopa zwrotu dała następujące wyniki:

Model         0.718    -0.433*P/BV(WIG20)
St. Error     (0.16)     (0.55) 

R^2adj. = 70.99% , R^2 = 78.24%  

Dla WIG20 parametry są nawet istotne statystycznie.

Dopasowanie prognozy stopy zwrotu (linia zielona) do faktycznej stopy zwrotu (linia niebieska) wygląda jak poniżej:

Na dzień dzisiejszy P/BV WIG20 wynosi 1,29. Jeśli pod koniec grudnia będzie podobna wartość, to możemy się spodziewać, że stopa zwrotu w 2013 r. wyniesie ok. 15,9%.
 
Oczywiście na spadek P/BV i wzrost stopy zwrotu w badanym okresie duży wpływ miała bessa od końca 2007, a to był akurat czas narodzin NewConnect. Trzeba jednak zaznaczyć, że P/BV NewConnect był na początku bardzo duży i spadał dużo szybciej niż WIG20: w końcu grudnia 2007 P/BV wyniósł ok. 40, podczas gdy rok później już 10 razy mniej. W tym czasie P/BV WIG20 spadł odpowiednio z 2,17 do 1,17, czyli do niecałe 2 razy mniejszej wartości. Można więc wnioskować, że wyższa niepewność i jej późniejszy spadek w przypadku Newconnect miały duże znaczenie dla spadku P/BV, niezależnie od bessy. 

Dlaczego ujemna zależność stopy zwrotu z P/BV jest dla WIG20 dużo silniejsza niż dla NC? Mam tutaj następujące wyjaśnienie. NC to mały rynek i nowe spółki zaburzają kapitalizację całego indeksu. Starsze spółki powinny mieć wyższą oczekiwaną stopę zwrotu, ale mogą być za małe w stosunku do nowych. W przypadku WIG20 nowe spółki są zbyt małe, by dostać się do pierwszej 20-tki. Im więcej będzie się pojawiało nowych spółek na NC, tym większy będzie hamulec dla większej stopy zwrotu dla tego indeksu.


Literatura:

[1] Pastor, L., and P. Veronesi. "Stock Valuation and Learning about Profitability." Journal of Finance, 58 (2003), 1749-1789.

Dane potrzebne dla sporządzenia statystyk do Newconnect i WIG20 zostały pobrane ze stooq.pl.

Czy większa niepewność zmniejsza stopę dyskontową?

Wnikliwy Czytelnik, który przeczytał dwa poprzednie artykuły, mógł zauważyć wzajemną ich sprzeczność.  W artykule Czy model Millera działa? Część 2  padł taki fragment:

"(...) na efektywnym rynku zwiększona niepewność prognozy zysku podnosi paradoksalnie wartość akcji (dokładniej zwiększa wskaźnik cena/wartość księgowa), a tym samym zmniejsza stopę zwrotu." 

Z kolei w Kiedy większa niepewność zwiększa wartość akcji? powiedziano, że większa niepewność (średniej) ROE podnosi wartość akcji pod warunkiem, że stopa dyskontowa jest niezależna od niepewności (średniej) ROE. Oczywiście niepewność prognozy zysku ściśle wiąże się z ROE. Czyli rzeczywiście to jest sprzeczność.   Dlatego poprawiłem tamto zdanie na:

"(...) na efektywnym rynku zwiększona niepewność prognozy zysku podnosi paradoksalnie wartość akcji (dokładniej zwiększa wskaźnik cena/wartość księgowa), a tym samym - zdaniem DKP - zmniejsza stopę zwrotu. (To czy DKP mają rację, należy omówić oddzielnie)."

Ale DKP, czyli Doukas, J.A., Kim C., Pantzalis [1] są w błędzie. Ironią losu jest to, że naukowcy mylą się w artykule, który wykazuje błędy innych naukowców. DKP albo nie mają dostatecznej wiedzy teoretycznej, albo bardzo powierzchownie przeczytali artykuł Pastora i Veronesiego (PV) [2]. Prawdopodobnie błędnie zasugerowali się innym twierdzeniem PV z tego samego artykułu, mianowicie, że stopa dyskontowa jest ujemnie skorelowana ze wskaźnikiem P/BV. Większa stopa dyskontowa może więc zmniejszyć P/BV, a mniejsza zwiększyć go. (Początkowo też sam błędnie napisałem w poprzednim artykule, że P/BV nie zmienia się wtedy - ten błąd też poprawiłem - tak już pisałem wcześniej w zagadnieniach teoretycznych ekonomii bardzo łatwo o błędy przez intuicję). Większa niepewność średniego ROE zwiększa P/BV, ale nie wpływa na stopę dyskontową. Oznacza to, że DKP nie wyjaśnili fenomenu polegającego na tym, że większa niepewność prognozy zysku zmniejsza stopę dyskontową (średnią stopę zwrotu). 

Przypomnijmy, że DKP wykryli najpierw błąd w hipotezie Millera [3], zgodnie z którą większa rozbieżność opinii o wartości akcji podnosi jej wartość. Miller przedstawił rysunek:




Gdy wszyscy się zgadzają co do wartości akcji (zysku), wartość wewnętrzna równa się G, czyli jest to linia prosta. Gdy rozbieżność opinii o wartości rośnie, krzywa popytu na akcje się wygina, tak że przy stałej podaży będącej liczbą akcji N, cena rynkowa wzrasta (M, R, Q). Bardziej optymistyczni w prognozach będą wyżej kupować akcje. Im większy optymizm, tym większa będzie sama cena akcji.

Miller założył, że inwestorzy posługują się ryzykiem subiektywnym, ale to sprawia, że są nieświadomi wyższej rozbieżności opinii. Większa rozbieżność  nie wpływa więc na postrzeganie ryzyka, tj.ryzyko nie zmienia się. Teraz przypomnijmy z poprzedniego artykułu zapis:





Zgodnie z teorią Millera pod wpływem większej bieżącej rozbieżności opinii zwiększy się wartość akcji P(0), ale ponieważ rozbieżność ta całkowicie zniknie w okresie T (bo firma zostanie zlikwidowana, a wtedy wartość akcji będzie się równać wartości księgowej - cały kapitał własny zostanie rozdzielony pomiędzy akcjonariuszy), to znaczy, że P(T) = BV(T) nie zmieni się. Ale skoro P(0) wzrasta, ale P(T) stoi w miejscu, to znaczy, że stopa dyskontowa r musi spaść! W ten sposób Miller chciał wykazać, że większa rozbieżność opinii zwiększa wartość akcji i jednocześnie zmniejsza stopę dyskontową, psując teorię CAPM.

Jednakże jeśli inwestorzy będą świadomi tej rozbieżności, to będzie ona stanowiła dodatkowe ryzyko systematyczne. To spowoduje, że stopa dyskontowa wzrośnie, a więc CAPM wcale się nie popsuje. Wzrost stopy dyskontowej powoduje spadek wartości akcji. 

Oba efekty (zmiana stopy dyskontowej i wpływ optymistów) zadziałają równocześnie przeciwko sobie, ale efekt stopy dyskontowej będzie silniejszy i wywoła spadek wartości akcji, a nie wzrost. Większa rozbieżność opinii zmniejsza więc wartość akcji i jednocześnie zwiększa stopę dyskontową. DKP w swoim badaniu empirycznym wykazali prawdziwość tej tezy.

Powyższą analizę przedstawiłem po to, aby uzmysłowić jaką logiką DKP prawdopodobnie się kierowali. Myśleli w ten sam sposób co Miller, tyle że zamienili "rozbieżność opinii" na "niepewność ROE". Myśleli, że dzisiejsza wartość akcji wzrośnie, ale w okresie T nie zmieni się. Ale w tym aspekcie to Miller miał rację, bo przyjął pewne założenia, których DKP nie dokonali (i nie mogli). Dziś już wiemy co się dzieje, gdy niepewność ROE (wariancja w zamieszczonym wyżej wzorze) rośnie: wzrasta przyszła wartość akcji, a ponieważ niepewność ROE nie wpływa w żaden sposób na stopę dyskontową r, bieżąca wartość akcji także wzrasta. 

Podsumowując, ciągle jeszcze nie wyjaśniliśmy fenomenu polegającego na tym, że mniej ryzykowne akcje (właściwie o mniejszej niepewności) generują (czy generowały) wyższe stopy zwrotu.


Literatura:

[1] Doukas, J.A., Kim C., Pantzalis C., "Divergence of Opinion and Equity Returns", 2006,
[2] Pastor, L., and P. Veronesi. "Stock Valuation and Learning about Profitability." Journal of Finance, 58 (2003), 1749-1789,
[3] Miller, E. - Risk, Uncertainty, and Divergence of Opinion, 1977.

Kiedy większa niepewność zwiększa wartość akcji?

Zazwyczaj uważa się, że wyższa niepewność na rynku obniża wartość rynkową akcji. Przyczyn tej obniżki dopatruje się we wzroście stopy dyskontowej oczekiwanych dywidend bądź przepływów pieniężnych. Tak jak zostało to pokazane w tym artykule model dyskontowy można powiązać z CAPM, zaś zgodnie z CAPM wyższe ryzyko systematyczne podnosi stopę dyskontową. Problem leży w tym, że niepewność to nie jest ryzyko systematyczne. Niepewność to nawet nie jest ryzyko. Ryzyko zazwyczaj utożsamiamy z odchyleniem standardowym stopy zwrotu. Ryzyko systematyczne akcji to ryzyko rynkowe, czyli jest to stosunek odchylenia standardowego stopy zwrotu z akcji do odchylenia standardowego stopy zwrotu z indeksu giełdowego razy współczynnik korelacji liniowej pomiędzy tą akcją a indeksem giełdowym. Jeśli odchylenie standardowe rośnie, to rośnie ryzyko systematyczne pod warunkiem, że korelacja z rynkiem się nie zmienia.

Z kolei niepewność to termin dość mglisty, bo niedookreślony. Zazwyczaj łączy się go z nieznanym rozkładem prawdopodobieństwa stopy zwrotu lub wskaźników finansowych. W tym miejscu powstaje wiele nieporozumień, bo trzeba dokładnie zdefiniować co rozumiemy przez niepewność, które dla inwestorów stało się słowem-wytrychem. Jeśli mówimy o niepewności stopy zwrotu, to musimy określić czy nieznana jest oczekiwana stopa stopa zwrotu czy nieznane jest ryzyko (odchylenie standardowe). Jednakże niepewność może też dotyczyć strony czysto fundamentalnej, jak np. rentowności kapitału własnego, tj. ROE. Wtedy musimy określić czy nieznane jest średnie ROE czy zmienność ROE.

Możemy więc wyróżnić 4 podstawowe przypadki wpływu parametrów na wartość akcji:
- od strony stopy zwrotu (przy innych czynnikach niezmienionych):
1. wzrost (spadek) oczekiwanej stopy zwrotu (stopy dyskontowej) -> spadek (wzrost) wartości akcji
2. wzrost (spadek) odchylenia standardowego (ryzyka) -> spadek (wzrost) wartości akcji

 - od strony ROE (przy innych czynnikach niezmienionych):
3. wzrost (spadek) oczekiwanego ROE -> wzrost (spadek) wartości akcji
4. wzrost (spadek) odchylenia standardowego ROE -> ???

Z tego wynika, że tylko wzrost lub spadek zmienności ROE ma niejasny wpływ na wartość akcji. Intuicyjnie może się wydawać, że wzrost zmienności ROE oznacza to samo co wzrost ryzyka stopy zwrotu, czyli spadek wartości akcji (przy ceteris paribus). Tyle że na intuicji nie zawsze można polegać.

L. Pastor i P. Veronesi w [1] wskazują, że dopóki zmienność ROE wynika z niesystematycznych, czyli nierynkowych przesłanek, wzrost (spadek) tej zmienności przynosi wzrost (spadek) wartości akcji. Wiadomo bowiem, że ROE składa się z dwóch części: systematycznej (czyli samej oczekiwanej stopy zwrotu) i niesystematycznej (czyli specyficznej dla danej spółki). Jeśli część niesystematyczna jest większa (mniejsza) od 0, to wartość akcji (P) jest większa (mniejsza) od wartości kapitału własnego na akcję (BV). Część niesystematyczna może składać się z premii za zmienność innowacyjnych przedsięwzięć. Nie chodzi tu tylko o premię za ryzyko niepowodzeń takich inwestycji, lecz także o fakt, że innowacje niosą ryzyko chwiejności wzrostu zysku - niektóre innowacje mogą przynosić większe, a inne mniejsze zyski. W każdym razie specyfika innowacji jest zupełnie niezależna od zachowania rynku jako całości. Oznacza to, że gdy rośnie ryzyko samych innowacji, stopa dyskontowa nie zmienia się.

Załóżmy, że spółka A zainwestowała w innowacje i generuje z niej zyski, a więc część niesystematyczna ROE jest większa od 0, co implikuje P(0) > BV(0). (Ponadto do okresu 0 do T spółka nie wypłaca dywidend). Jednakże w pewnym okresie T część niesystematyczna spada do 0, czyli spółka nie jest już w stanie generować innowacji, "premia za ryzyko innowacji" spada do 0, a więc P(T) = BV(T). Uzasadnić to można w ten sposób, że konkurencja rozwija własne pomysły, eliminując tym samym zyski nadzwyczajne firmy A. Od okresu 0 do T, BV(t) rośnie w pewnym stałym tempie g. Wartość g można potraktować jako wartość oczekiwaną stopy wzrostu, gdyż w rzeczywistości stopa wzrostu podlega różnym wahaniom, czyli jest zmienną losową. W okresie T BV(T) wynosi:

Ponieważ wzrost BV(t) jest średnio stały w czasie, nic nie stoi na przeszkodzie, by potraktować go jako proces ciągły w czasie. Najpierw każdy okres t podzielimy na n podokresów i każdy podokres będzie kapitalizowany. Stopę procentową g podzielimy także na n, po to aby otrzymać tempo wzrostu w danym podokresie. (Będzie to prawidłowe pod warunkiem, że g będzie logarytmiczną stopą wzrostu - to z kolei nie jest niczym nadzwyczajnym, gdyż pojęcie stóp procentowych jakie znamy odnosi się właśnie do logarytmicznych a nie arytmetycznych stóp wzrostu w celu umożliwienia szybkiego obliczania kapitalizacji półrocznej, kwartalnej, miesięcznej itd):

Jeśli liczba podokresów n dąży do nieskończoności:

to możemy skorzystać ze znanego wzoru:

I w ten sposób przechodzimy z kapitalizacji nieciągłej na ciągłą:

Choć g potraktowaliśmy jako wartość oczekiwaną tempa wzrostu, to w rzeczywistości wartość ta nie jest znana, czyli również jest zmienną losową. Od okresu 0 do T została "wylosowana" pewna wartość g. Możemy w uproszczeniu uznać g za zmienną o rozkładzie normalnym z wartością oczekiwaną G i wariancją σ^2. Czyli BV(T) staje się wartością oczekiwaną:

Ale jeśli g ma rozkład normalny, to exp(g) ma rozkład logarytmiczno-normalny . Z kolei wartość oczekiwana zmiennej o rozkładzie logarytmiczno-normalnym jest dana wzorem [2],[3]:

Czyli dostaniemy:

Zauważmy teraz, że jeśli zdyskontujemy wartość BV(T) T okresów za pomocą stopy dyskontowej r, to uzyskamy P(0). Wykorzystując analogiczne przekształcenia przejścia od kapitalizacji nieciągłej do ciągłej dla stopy dyskontowej, uzyskujemy wzór na wartość akcji P(0):

Możemy również przedstawić wskaźnik P/BV w następującej postaci:

Zwróćmy uwagę, że gdy wzrasta odchylenie standardowe g, to wzrasta P/BV. Co ciekawe, wtedy BV nie zmienia się. Ponieważ g stanowi nie tyle wartość oczekiwaną co zmienną losową (wartości oczekiwanej) tempa wzrostu o pewnych parametrach, to mówiąc o odchyleniu standardowym g jesteśmy już blisko tego co nazywamy właśnie "niepewnością". A więc możemy powiedzieć, że gdy rośnie niepewność zysków nadzwyczajnych (nadwyżkowych monopolistycznych), wzrasta wartość fundamentalna akcji, a wartość księgowa nie zmienia się.

Aby zrozumieć jaki mechanizm tutaj działa, zilustrujemy go następującym przykładem podanym przez Pastora i Veronesiego. Załóżmy, że firmy A i B różnią się tylko przyszłym tempem wzrostu ich wartości księgowej, której bieżąca wartość wynosi 1 mln zł. Gdy A zamierza wzrastać 10% na rok z prawdopodobieństwem 1, B wzrasta albo w tempie 5%, albo 15% na rok z równym prawdopodobieństwem. I tak w ciągu 10 lat 1 mln zł kumuluje się do 4,05 mln zł przy 15%, do 2,59 mln zł przy 10% i do 1,63 mln zł przy 5%. Wtedy firma B ma wyższą oczekiwaną przyszłą wartość księgową niż A, bo (4,05 + 1,63) / 2 = 2,84 > 2,59.

Należy tu ciągle pamiętać, że stopa dyskontowa r wyrażająca premię za ryzyko systematyczne pozostaje stała, bo zyski monopolistyczne-nadwyżkowe nie korelują z zyskami konkurencji rynkowej. Należy zauważyć, że g to nie jest nadwyżkowa stopa wzrostu, lecz całkowita. To oznacza, że niepewność σ^2 zawiera częściowo zarówno ryzyko systematyczne jak i niesystematyczne. Należy więc tutaj rozróżnić dwie sytuacje.
 Po pierwsze może wzrosnąć (spaść) tylko ryzyko systematyczne. Wpływ tego zdarzenia na P/BV wymaga oddzielnego komentarza i zastanowienia. Po drugie może wzrosnąć tylko ryzyko niesystematyczne (specyficzne). Ten przypadek został powyżej dokładnie omówiony.

Jak pamiętamy g ściśle wiąże się z ROE. Ponieważ g oznacza dokładnie stopę wzrostu wartości księgowej, a nie zysku, to znaczy, że g = k*ROE, gdzie
k - część zysku netto z okresu bieżącego zwiększająca kapitał własny z okresu poprzedniego..

Przypomnijmy może skąd ten wzór wynika:

BV(t) = BV(t-1) + k*ZYSK(t) =  BV(t-1)*(1+k*ZYSK(t) / BV(t-1)) = BV(t-1)*(1 + k*ROE) = BV(t-1)*(1 + g) => g = k*ROE.

Zmienność g będzie ściśle związana ze zmiennością ROE. Ale ponieważ g charakteryzuje się też niepewnością, to i ROE charakteryzuje się niepewnością. Ogólnie stwierdzamy, że zmienność czy niepewność o średniej ROE zwiększa P/BV.
Jednak błędem jest twierdzenie, że większa zmienność ROE zwiększa P/BV. Wcześniej zostało wskazane, że nie może to być ryzyko systematyczne. Dopiero wzrost ryzyka niesystematycznego wpłynie dodatnio. Zmiany średniej ROE mamy z kolei prawo uznać jako nieskorelowane z ryzykiem systematycznym.

Powyższa analiza stanowi jedynie wstęp do rozbudowanego modelu Pastora i Veronesiego, którzy dalej wprowadzają model, w którym rynek uczy się, czego należy się spodziewać po spółce. Z pomocą przychodzi wtedy warunkowa zmienna losowa, której parametry są zależne od przeszłych wartości. Prowadzi to do wniosku, że największa warunkowa niepewność (średniego) ROE występuje w początkowych fazach życia firmy, co prowadzi do wyższego P/BV w tym okresie (a więc w późniejszej fazie życia P/BV staje się niższy). Ponadto Autorzy rozróżniają sytuacje, gdy spółka wypłaca i nie wypłaca dywidend. Model zgodnie z intuicją wskazuje, że większa niepewność występuje w przypadku firm niepłacących dywidend, a więc te powinny mieć wyższe P/BV. Autorzy stawiają też sugestię, że duże wartości P/BV wielu spółek z giełdy w USA pod koniec lat 90-tych mogły wynikać z tej większej niepewności, zamiast braku racjonalności rynku.
Przykładowo poniższy wykres obrazuje modelową zależność pomiędzy niepewnością o średniej ROE (oś pozioma) a wskaźnikiem P/BV (oś pionowa):

Literka c oznacza część wartości księgowej (BV), którą spółka wypłaca akcjonariuszom w postaci dywidendy. Widać, że im mniejsza dywidenda, tym większe P/BV.

W końcu również empirycznie dowodzą oni swoich tez, wykorzystując regresję liniową. Do badania użyli rocznych danych od 1962 do 2000 r. z CRSP/Compustat database. Zbudowana regresja w dużym stopniu potwierdziła przewidywania modelu teoretycznego.


Literatura:
[1] Pastor, L., and P. Veronesi. "Stock Valuation and Learning about Profitability." Journal of Finance, 58 (2003), 1749-1789;
[2] http://en.wikipedia.org/wiki/Log-normal_distribution;
[3] Ossowski, J. C., "Rozkład logarytmiczno-normalny a względne i absolutne miary rozproszenia", Toruń 2003.

Czy model Millera działa? Część 2

W ekonomii, jak we wszystkich naukach ścisłych, należy uważać na każde słowo, a jeszcze bardziej na wypowiadane sądy. Nieuwzględnienie pewnych czynników, np. ukrytych założeń, prowadzi często do błędnego wnioskowania. Błędy mogą być dwojakiego rodzaju. Pierwszy błąd powstaje gdy dana teoria czegoś istotnego nie uwzględnia, a drugi błąd, gdy metody badawcze czegoś istotnego nie uwzględniają. Pierwszy błąd łatwo wykryć pod warunkiem, że nie występuje drugi błąd, gdyż wtedy teoria nie zgadza się z doświadczeniem. Gorzej jeśli drugi błąd nie został wykryty, bo wtedy teoria/teza może się wydawać prawdziwa, podczas gdy w rzeczywistości jest fałszywa. Tak więc weryfikacja teorii powinna zawsze zaczynać się od weryfikacji samych metod badawczych.

Weryfikacja modelu Millera stanowi właśnie przykład, gdzie mogą pojawić się błędy obydwu rodzajów. W pierwszej części artykułu poświęconemu weryfikacji teorii Millera, przedstawiłem wyniki badań Diether, Malloy i Scherbiny [1] (DMS), które potwierdziły ją empirycznie. Sytuacja jednak okazuje się dużo bardziej skomplikowana niż to na pierwszy rzut oka wygląda. Przypomnijmy, że teoria Millera przewiduje, że wyższa rozbieżność opinii na temat wartości akcji generuje wyższą wartość akcji, a co za tym idzie mniejsze oczekiwane stopy zwrotu w przyszłości. Ponieważ wartość akcji ściśle zależy od oczekiwanych zysków netto spółki, pośrednikiem rozbieżności opinii o wartości akcji może być rozbieżność opinii o oczekiwanych zyskach netto. Za pośredników inwestorów szacujących te zyski możemy uznać analityków giełdowych. Wydaje się prawidłowe, że rozbieżność taką można obliczyć jako odchylenie standardowe prognoz zysków (szacowanych przez analityków).

Jednak diabeł tkwi jak zawsze w szczegółach. Wahania wyników finansowych zależą w głównej mierze od branży w jakiej spółka funkcjonuje. Np. spółki farmaceutyczne będą niewątpliwie "bezpieczniejsze" od spółek, których wyniki zależą w dużym stopniu od cen surowców. Oznacza to, że sama natura spółek o mniejszym zakresie wahań wyników spowoduje, że oczekiwania wyników będą mniej "rozbieżne" (rozstrzelone). Ten fakt został pominięty przez DMS, na co zwracają uwagę Doukas, Kim i Pantzalis [2] (DKP).

Autorzy podają najpierw teoretyczne uzasadnienie tego błędu wprowadzone przez Barrona, Kima, Lima i Stevensa [3], którzy pokazują, że dyspersja (wariancja) prognoz może być wyrażona w postaci D = V(1-p), gdzie V to niepewność prognozy, a 1-p to rozbieżność opinii analityków, natomiast p to konsensus (stopień zbieżności opinii analityków), który stanowi współczynnik korelacji błędów prognozy wśród analityków. Należy zwrócić uwagę, że wzór został odpowiednio wyprowadzony.

Widzimy więc, że dyspersja prognoz analityków została rozbita na dwie części: zwyczajne ryzyko oraz stopień braku konsensusu prognozy. Jeśli dana branża będzie bardziej ryzykowna, będzie rosło V. Jeśli analitycy będą mniej zgodni w swoich przewidywaniach, wzrośnie 1-p. Jeśli wszyscy będą zgodni w 100%, czyli p = 1, to D = 0, a więc nie będzie istnieć zróżnicowanie prognoz. Jeśli analitycy będą mieć różne nieskorelowane zdania, to p = 0, a stąd D = V, a więc zróżnicowanie prognoz będzie równe zwykłej niepewności prognozy związanej ze zmiennością wyników danej spółki. Jeśli analitycy będą mieć ekstremalnie różne zdania, to p = -1, a stąd D = 2V, tj. zróżnicowanie prognoz podwaja się w stosunku do zwykłej niepewności. DMS posługiwali się całkowitą dyspersją D jako pośrednikiem rozbieżności opinii o wartości akcji, a więc można powiedzieć, że zakładali stałość V. Jednak V zmienia się w zależności od specyfiki branży czy samej spółki, zatem D raczej słabo odzwierciedla faktyczną rozbieżność opinii. DKP stwierdzają, że do testu modelu Millera należy użyć 1-p, gdyż jest to faktyczna miara rozbieżności prognoz zysku.

DKP pobierali, podobnie jak DMS, dane z Institutional Brokers Estimate System. Zakres badania zawiera się w podobnym przedziale co DMS, bo od lipca 1983 do grudnia 2001. Najpierw powtórzono metodę zastosowaną przez DMS. Tak więc dyspersja prognoz analityków została obliczona jako wyskalowane odchylenie standardowe prognoz zysków (tzn. odchylenie standardowe prognoz rocznego zysku podzielone przez moduł średniej prognozy). Następnie podzielono te dyspersje na 5 grup, według wielkości dyspersji: od najmniejszej do największej (kwintyle). Podobnie zostały uszeregowane akcje według wielkości kapitalizacji, dzięki czemu można ocenić wpływ dyspersji na stopy zwrotu dla różnych wielkości spółek. Wyniki zostały zaprezentowane w tabeli poniżej - średnie miesięczne stopy zwrotu w zależności od wielkości spółki (SIZE) oraz dyspersji prognoz zysków (D).

***, **, * oznacza odpowiednio istotność statystyczną na poziomie 1%, 5% i 10%.

Wyniki są zbieżne z otrzymanymi przez DMS. Po pierwsze większa dyspersja prognoz wiąże się z mniejszą stopą zwrotu, dla każdej grupy spółek. Jest to wynik nawet bardziej poprawny z punktu widzenia modelu Millera niż w badaniu DMS. Następnie przeprowadzono ten sam test, ale tym razem sprawdzono zachowanie stóp zwrotu w zależności od (1-p). Otrzymano następujące wyniki:

Rezultaty zmieniają się o 180 stopni. Większej rozbieżności prognoz towarzyszy istotnie większa średnia stopa stopa zwrotu, dla każdej grupy spółek. Wynika z tego, że cały efekt spadku stopy zwrotu wraz ze wzrostem dyspersji wynika z niepewności prognozy V, który kompensuje dodatni wpływ rozbieżności. Zatem większa niepewność prognozy prowadzi do spadku średniej stopy zwrotu, a większa rozbieżność opinii do wzrostu stopy zwrotu.

Rodzą się więc nowe pytania. Dlaczego rozbieżność opinii prowadzi do wzrostu stopy zwrotu? DKP stawiają hipotezę, że rozbieżność opinii stanowi jeden z czynników ryzyka systematycznego (rynkowego), a wyższe ryzyko systematyczne implikuje wyższą oczekiwaną stopę zwrotu. Swoją hipotezę weryfikują budując wieloczynnikowy model wyceny aktywów (rozbudowany model Famy-Frencha), będący modyfikacją CAPM. Hipoteza zdaje test, gdyż rozbieżność opinii okazuje się być istotnym czynnikiem w modelu, a więc prawdopodobnie stanowi czynnik ryzyka dla inwestora.

Kolejne pytanie jakie się nasuwa to: dlaczego wzrost niepewności prognozy prowadzi do spadku stopy zwrotu (wzrostu wartości akcji) i czy nie jest to anomalia sprzeczna z teorią efektywności rynku i CAPM? Na pierwszy rzut oka wydaje się to być faktycznie sprzeczne, gdyż niepewność to po prostu ryzyko, a przecież ryzyko w teorii portfela, CAPM i jego modyfikacji zawsze stanowi koszt inwestora, który w zamian wymaga wyższej stopy zwrotu. Ale samo ryzyko jest pojęciem względnym. W teorii portfela większa wariancja akcji nie implikuje wyższej stopy zwrotu. Dopiero wariancja portfela efektywnego implikuje wyższą oczekiwaną stopę zwrotu. Mówiąc ściślej tylko ryzyko systematyczne (rynkowe) kreuje wyższą oczekiwaną stopę zwrotu, ponieważ jest niedywersyfikowalne. Z kolei ryzyko specyficzne, czyli właśnie wariancja dowolnej akcji jest ryzykiem dywersyfikowalnym, a przez to nie generuje automatycznie oczekiwanej stopy zwrotu.

Jednak taka odpowiedź byłaby nieprzekonująca. W końcu rezultaty statystyczne wskazują na istotną ujemną korelację pomiędzy stopą zwrotu a niepewnością prognozy, a klasyczne teorie tego nie tłumaczą. DKP odpowiadają na to pytanie nawiązując do stosunkowo nowego artykułu Pastora i Veronesi'ego [4], którzy z kolei dowodzą, że na efektywnym rynku zwiększona niepewność prognozy zysku podnosi paradoksalnie wartość akcji (dokładniej zwiększa wskaźnik cena/wartość księgowa), a tym samym - zdaniem DKP - zmniejsza stopę zwrotu. (To czy DKP mają rację, należy omówić oddzielnie). DKP argumentują, że stanowisko DMS było błędne, bo ich badanie nie potwierdziło teorii Millera. Wszystkie wyniki statystyczne można ciągle wyjaśnić na gruncie teorii efektywnego rynku. Zdaje się, że model Millera trzeba odrzucić, bo wyższa wartość rynkowa akcji nie wynika z większej rozbieżności opinii o wartości wewnętrznej, lecz z większej niepewności prognozy - ale to jak niepewność może zwiększyć wartość akcji stanowi oddzielny temat.


Dodatek:

p i V zostały obliczone następująco:

gdzie

h jest to precyzja zwykłej, wspólnej informacji, s jest to precyzja prywatnej informacji (opinii)

gdzie
y - faktyczny prognozowany zysk (EPS),
u(i) - prognoza i-tego analityka
u - średnia prognoz wszystkich analityków
N - liczba analityków (prognoz).


Literatura:

[1] Diether, K, B; C, J, Malloy; A, Scherbina; "Differences of Opinion and the Cross Section of Stock Returns", 2002
[2] Doukas, J.A., Kim C., Pantzalis C., "Divergence of Opinion and Equity Returns", 2006
[3] Barron, O, E,; O, Kim; S, C, Lim; and D, E, Stevens, "Using Analysts' Forecasts to Measure Properties of Analysts' Information Environment," Accounting Review, 73 (1998), 421-433,
[4] Pastor, L., and P. Veronesi. "Stock Valuation and Learning about Profitability." Journal of Finance, 58 (2003), 1749-1789.

Czy model Millera działa? Część 1

Zgodnie z modelem Millera (który został opisany w artykule Rozbieżność opinii, nieefektywność rynku i trendy akcji, czyli model Millera) większa rozbieżność opinii na temat wartości akcji powoduje (przy założeniu, że krótka sprzedaż jest ograniczona) wzrost ceny rynkowej akcji, a co za tym idzie spadek stopy zwrotu.

Model Millera można starać się przeanalizować pod kątem formalnym, aby znaleźć jego słabe punkty. Ukryte założenia lub intuicje zawsze wychodzą na wierzch, jeśli zagadnienie bada się ścisłym językiem.

Na tym etapie skoncentrujmy się jednak na najważniejszej, czyli praktycznej stronie modelu Millera. Diether, Malloy i Scherbina (2002) testują go doświadczalnie. Początkowe pytanie przy jego testowaniu jest takie: jak w ogóle mierzyć rozbieżność opinii na temat wartości akcji? Wartość akcji jest to suma zdyskontowanych oczekiwanych dywidend. Jak już dowiedziono, wartość akcji jest to jednocześnie suma zdyskontowanych oczekiwanych przepływów pieniężnych: jest to Uogólniony model Grahama-Dodda , w skrócie UMGD. Zgodnie z UMGD na wartość akcji wpływają trzy zmienne: oczekiwane zyski netto firmy, oczekiwane inwestycje oraz koszt kapitału własnego. Decydującym i najbardziej zmiennym przy szacunkach czynnikiem są zyski. Zatem pośrednikiem rozbieżności opinii o wartości akcji jest rozbieżność opinii o prognozowanych zyskach firmy. Z kolei za pośredników inwestorów szacujących te zyski możemy uznać analityków giełdowych. Im większa będzie rozbieżność analityków w prognozach zysków, tym większa będzie rozbieżność w ocenie wartości akcji.

Autorzy omawianego artykułu pobierali miesięczne stopy zwrotu z Center for Research in Securities Prices (CRSP), który zawiera dane NYSE, AMEX i Nasdaq. Dane analityków o prognozach zysków zostały wzięte z Institutional Brokers Estimate System (IBES). Test został przeprowadzony dla okresu luty 1983 - grudzień 2000.

Dyspersja prognoz analityków została obliczona jako wyskalowane odchylenie standardowe prognoz zysków (tzn. odchylenie standardowe prognoz rocznego zysku podzielone przez moduł średniej prognozy). Następnie podzielono te dyspersje na 5 grup, według wielkości dyspersji: od najmniejszej do największej (kwintyle). Podobnie zostały uszeregowane akcje według wielkości kapitalizacji, dzięki czemu można także ocenić efekt małych czy dużych spółek. Wnioski zostały zaprezentowane w formie różnych tabel. Poniżej pierwsza z nich:



a, b - istotne statystycznie na poziomie odpowiednio 1 i 5%.

Najpierw przypatrzmy się prawej stronie tabeli, gdzie ujęte są wszystkie akcje (All stocks). Im większa dyspersja (D), tym mniejsza średnia stopa zwrotu (Mean Returns). Teraz możemy przejść do kolejnych grup według wielkości spółek. Najmniejsze spółki (Small) charakteryzują się bardzo silną ujemną korelacją pomiędzy dyspersją a stopą zwrotu. Największe spółki (Large) charakteryzują się już dużo mniejszą taką nagatywną relacją i jak widać jest już ona nieistotna statystycznie.

Dla pełniejszego obrazu Autorzy sporządzili ten sam test dla 3 podokresów.



Sytuacja tutaj bardziej się komplikuje. Efekt dla najmniejszych spółek S1 nadal jest silny, jednak już większe spółki stają się coraz bardziej odporne i tracą istotność. Możliwe, że dzieje się tak, ponieważ większe spółki są bardziej eksponowane i lepiej obserwowane, a więc inwestorzy mogli zacząć wykorzystywać zaobserwowane zależności. Być może jednak chodzi o to, że informacje zaczęły być w latach 80 i 90-tych coraz łatwiej dostępne, w szczególności dla większych spółek. To spowodowało, że inwestorzy lepiej szacowali przyszłe zyski, stąd rozbieżności tych prognoz stały się mniejsze, co z kolei musiało skutkować spadkiem stopy zwrotu (efekt rozbieżności stał się nieistotny).

Warto zasygnalizować, że Autorzy dodatkowo także dla pełniejszego obrazu zrobili test tylko dla spółek z NYSE. Efekt jest podobny, wyniki spółek o mniejszej kapitalizacji mają większą istotność stat.

Autorzy dodatkowo testują teorię Millera w kontekście efektu momentum. Dzielą spółki na małe, średnie i duże, a następnie wszystkie na 3 grupy o stopie zwrotu w ostatnim roku: o najniższej, średniej i najwyższej. "Przegrani" (Losers) stanowią grupę 33% najgorzej zachowujących się akcji, a "Wygrani" (Winners) grupę 33% najlepiej zachowujących się akcji. Oto wyniki:



Pomimo że Autorzy nie badają istotności statystycznej efektu momentum, możemy zauważyć "naocznie", że taki efekt występował. Zarówno małe, średnie, jak i duże spółki mają najniższe średnie stopy zwrotu gdy występują w grupie Losers i najwyższe gdy występują w grupie Winners. Oznacza to, że spółki które gorzej zachowywały się w ostatnim roku, będą również gorzej zachowywać się w kolejnym miesiącu. A spółki które lepiej zachowywały się w ostatnim roku, będą również lepiej zachowywać się w kolejnym miesiącu. Wszystko to dzieje się niezależnie od dyspersji prognoz.

Wpływ samej dyspersji na stopy zwrotu staje się bardziej skomplikowany. Istotna statystycznie ujemna korelacja występuje jedynie dla małych spółek, które nie należą do grupy Winners. Pomimo braku istotności dla Mid-Cap i Large-Cap, dla Losers i środkowej grupy nadal utrzymuje się ujemna zależność. Większa dyspersja ciągle wywołuje mniejszą stopę zwrotu. Ten efekt dopiero psuje się całkowicie dla Winners. Co więcej, dla Small-Cap negatywny wpływ dyspersji także jest tajemniczo słaby. Pytanie co może powodować usunięcie efektu dyspersji? Wprawdzie Autorzy podają różne rozwiązania i podpowiedzi, ale zamiast tego przypomnimy sobie jak wyjaśniłem ostatnio powstanie trendu, czyli właśnie efektu momentum na gruncie teorii Millera.

Wniosek z teorii był taki, że okres wzrastającej rozbieżności opinii podnosi natychmiastowo kurs, co powoduje, że późniejsza stopa zwrotu spada. Ale sam okres wzrostu rozbieżności opinii przynosi oczywiście wyższe stopy zwrotu.

Aby połączyć to z całością teorii, musimy rozbić sytuację na dwa efekty:

- rozbieżność opinii może być sama w sobie wyższa, jeśli informacje są mniej dostępne, jak w przypadku małych spółek. To sprawia, że kurs akcji jest wyższy, ale oczekiwana stopa zwrotu jako taka jest mniejsza,
- rozbieżność opinii może rosnąć lub spadać. Jeśli rośnie, to kurs podnosi się i wtedy dopiero w następnym okresie stopa zwrotu spada. Jeśli z kolei rozbieżność opinii spada, to kurs spada i wtedy dopiero w następnym okresie stopa zwrotu rośnie.

Oba efekty mogą się niwelować lub wzmacniać i tym samym wywoływać różne paradoksalne zjawiska.

W przypadku Losers dla małych spółek trend jest spadkowy lub słabo wzrostowy, bo np. rozbieżność opinii spada. Kurs spada (nie rośnie), oczekiwana stopa zwrotu w kolejnym okresie rośnie, ale jej wzrost jest hamowany przez większą ogólną rozbieżność opinii ze względu na to, że są to małe spółki. W konsekwencji średnia stopa zwrotu pozostaje niewielka (i efekt pozostaje bardzo istotny stat.).
Jednak dla większej spółki (większej kapitalizacji) rozbieżność opinii nie jest tak duża, co powoduje, że stopa zwrotu rośnie. Wtedy - pomimo słabości kursu waloru - przyszła stopa zwrotu może się utrzymywać na wyższym poziomie, powodując nieistotność ujemnej korelacji z rozbieżnością opinii.

W przypadku Winners dla małych spółek trend jest wyraźnie wzrostowy, bo np. rozbieżność opinii rośnie. Kurs rośnie, oczekiwana stopa zwrotu w kolejnym okresie spada, co zostaje wzmocnione przez fakt, iż dla małych spółek rozbieżność opinii jest większa. Ale ponieważ rozbieżność opinii ciągle rośnie, tak że trend wzrostowy się utrzymuje, spadek stopy zwrotu zostaje zahamowany. Stąd ujemna korelacja stopy zwrotu z rozbieżnością opinii staje się słabsza (przestaje być istotna stat).
W przypadku większych spółek rozbieżność opinii jest z natury mniejsza, a więc stopa zwrotu utrzymuje się na wyższym poziomie. Dodatkowo sam wzrost rozbieżności opinii wzmacnia stopę zwrotu w bieżącym okresie. To powoduje, że dla Winners (pozytywnego momentum) stopa zwrotu większych spółek nie koreluje z rozbieżnością opinii lub nawet korelacja ta wydaje się dodatnia.

Przypomnijmy obrazek ilustrujący ideę Millera:



Gdy wszyscy się zgadzają co do wartości akcji (zysku), wartość wewnętrzna równa się G, czyli jest to linia prosta. Gdy rozbieżność opinii o wartości rośnie, krzywa popytu na akcje się wygina, tak że przy stałej podaży będącej liczbą akcji N, cena rynkowa wzrasta (M, R, Q).

W ten sposób można wyjaśnić niejednoznaczne wyniki statystyczne badaczy przy diagnozie momentum.

Na postawione pytanie w tytule Autorzy odpowiadają oczywiście twierdząco, a więc teoria Millera sprawdza się w praktyce.

Na koniec tego artykułu należy zasygnalizować, że choć cała odkryta statystyczna strona modelu Millera wydaje się pociągająca, prawdziwa i niosąca pewne implikacje praktyczne, to inni Autorzy jak John A. Doukas, Chansog (Francis) Kim i Christos Pantzalis (2006) negują te wyniki, przedstawiają własne, które są przeciwne i argumentują, że model Millera wcale się nie sprawdza. I nie chodzi tu o błędy obliczeń. To odmienne stanowisko zostanie opisane w następnym artykule.


Literatura:

1. Diether, K, B; C, J, Malloy; A, Scherbina; "Differences of Opinion and the Cross Section of Stock Returns", 2002
2. Doukas, J.A., Kim C., Pantzalis C., "Divergence of Opinion and Equity Returns", 2006.

Rozbieżność opinii, nieefektywność rynku i trendy akcji, czyli model Millera

Czy rozbieżność oczekiwań wśród inwestorów na temat przyszłych zysków, dywidend, stóp zwrotu i ryzyka wiąże się w jakiś sposób z kształtowaniem się trendów kursów akcji? Wiadomo z poprzedniego artykułu Rozbieżność opinii w kontekście CAPM , że sama rozbieżność opinii niewiele zmienia i rynek może pozostać całkowicie efektywny. Wcześniej jednak powiedziałem, że asymetria informacji w połączeniu z rozbieżnością oczekiwań i ich wzajemne sprzężenia są w stanie wywołać trend, nawet długoterminowy. Oczywiście długość trendu będzie zależeć od czynników fundamentalnych.

Edward E. Miller w artykule z 1977 r. "Risk, Uncertainty, and Divergence of Opinion" zaproponował interesujący model wyjaśniający różnego rodzaju "dziwne" zachowania stóp zwrotu przeczące teorii efektywności rynku oraz CAPM związany z rozbieżnością opinii inwestorów.

Rozważmy uproszczony model, w którym spółka akcyjna organizuje projekt na jeden rok. Po roku spółka zostanie zlikwidowana, a jej aktywa zostaną podzielone pomiędzy inwestorów. Inwestorzy maksymalizują oczekiwaną stopę zwrotu przy danym ryzyku, estymują stopę zwrotu z inwestycji, ale z powodu niepewności różnią tymi estymacjami.

Poniższy wykres pokazuje skumulowany rozkład liczby inwestorów z estymacjami powyżej pewnej wartości otrzymanej przy likwidacji inwestycji. Może być on także interpretowany jako liczba akcji, którą chcą trzymać inwestorzy po danej cenie.



Załóżmy, że każdy inwestor jest w stanie trzymać tylko jedną akcję i jest N dostępnych akcji. Na krzywej ABC widać, że N inwestorów szacuje końcową wartość R lub wyższą. W sumie cena sprzedaży ustala się na poziomie R. Jeśli cena wyniesie mniej niż R, będzie więcej niż N inwestorów którzy chcą trzymać akcje, ale ponieważ akcji w obrocie jest tylko N, zaczną pomiędzy sobą rywalizować, podbijając maksymalnie cenę do R. Jeśli cena będzie powyżej R, wtedy będzie mniej niż N inwestorów, którzy chcą trzymać akcje, a ponieważ liczba akcji N jest większa, podaż będzie zmuszona do sprzedawania akcji, sprowadzając cenę do R.

Aby lepiej zrozumieć model, przypomnijmy sobie poprzedni artykuł, gdzie podałem wzór na oczekiwaną przyszłą cenę akcji. Mieliśmy cenę P(0) w momencie 0 i E(P(1)) w okresie 1. Jeśli więc zaczynamy od okresu 0, to oczywiście inwestorzy kupują akcje po P(0), w tym przypadku po jednej akcji. P(0) może się znajdować w dowolnym punkcie krzywej ABC. Ale każdy inwestor może szacować inny poziom E(P(1)). Jeśli P(0) znajduje się poniżej R, to będzie więcej niż N inwestorów (czyli więcej niż akcji w obrocie), którzy chcą teraz trzymać akcje, ponieważ uważają, że w okresie 1 cena wyniesie co najmniej R lub - co na jedno wychodzi - dostaną przy likwidacji wartość kapitału własnego na jedną akcję równą R lub wyższą, co że pozwoli im maksymalizować stopę zwrotu. Jeśli bieżąca cena P(0) okaże się równa bądź wyższa od R, to inwestycja przestanie być opłacalna dla części z tych inwestorów. Ta część "odpadnie", w tym sensie, że ci, którzy kupili akcje po niższej cenie, będą sprzedawać, a ci którzy nie kupili, nie będą chcieli już kupić. W ten sposób pozostanie mniejsza liczba inwestorów, która nadal uważa, że przy danej cenie inwestycja maksymalizuje ich stopę zwrotu. W tej mniejszej grupie ci, którzy już kupili akcje wcześniej, nadal trzymają, a ci którzy nie kupili, będą starać się ciągle kupić. Ta grupa nadal bowiem uważa, że w okresie 1 cena będzie zadowalająco wyższa. Ale wraz ze wzrostem bieżącej ceny P(0) liczba tych inwestorów będzie sukcesywnie spadać. Stąd przesuwając się z prawej do lewej liczba inwestorów spada, a cena rośnie.

Jeśli pominiemy inne spółki w analizie, możemy stwierdzić, że inwestorzy będą kupować akcje dopóki szacowana stopa zwrotu przewyższy stopę zwrotu z obligacji rządowych po uwzględnieniu ryzyka. Ponieważ każdy może inaczej oceniać ryzyko i oczekiwaną stopę zwrotu, to każdy może mieć inny poziom akceptowalnej ceny zakupu i sprzedaży. A więc na osi pionowej znajdują się jednocześnie ceny zakupu P(0) i ceny oczekiwane E(P(1)) różnych inwestorów. Oczywiście jeśli wartość E(P(1)) szacowana przez pewną grupę inwestorów zostanie osiągnięta przed okresem likwidacji, to będzie mogła już realizować zysk.

Na krzywą ABC można spojrzeć jak na krzywą popytu, gdzie dana liczba inwestorów odpowiada popytowi przy danej cenie. Krzywa podaży jest to linia pionowa N wyrażająca liczbę dostępnych akcji.

Oczywiście łatwo zauważyć, że w takim układzie przyszła cena R będzie musiała zostać bardzo szybko osiągnięta, ponieważ cena jest wynikiem sił popytu i podaży. Dzieje się tak dlatego, że pewna stosunkowo niewielka (jak widać na wykresie) grupa inwestorów, ale będąca jeszcze w stanie zaspokoić całkowitą podaż, ciągle uważa, że przy P(0) = R, inwestycja jest nadal opłacalna.

Ta niewielka grupa inwestorów dopóki będzie w stanie wchłonąć podaż, spowoduje, że cena rynkowa będzie wyższa niż średnia oczekiwana cena przez ogół inwestorów. (Przy czym oczekiwana cena R będzie nadal średnią ważoną udziałem akcji, a tym samym estymacji wielu inwestorów tak jak przedstawiono to w poprzednim artykule). Zatem najwięksi optymiści albo słabo lub lepiej poinformowani będą w stanie spowodować istotne zwyżki kursu.

Dopiero nowe informacje płynące z otoczenia rynkowego czy samej spółki wpłyną na zmiany jej wyceny. I wszystko zacznie się od nowa, aż do momentu likwidacji spółki.

Rozbieżność opinii może się zmieniać w czasie pod wpływem nowych informacji. Co więcej, jak Miller stwierdza, rozbieżność opinii na temat stopy zwrotu i ryzyko zmieniają się w tym samym kierunku. Znaczenie ma tutaj założenie, że rzeczywiste inwestycje charakteryzują się niepewnością, to znaczy rozkład prawdopodobieństwa zdarzeń jest nieznany. Skutkuje to tym, że decyzje opierają się na subiektywnych szacunkach przyszłych zdarzeń, na subiektywnych prawdopodobieństwach. W grach hazardowych jak kasyno można ściśle wyznaczyć ryzyko i rozkład prawdopodobieństwa, a więc nie istnieje niepewność, a tym samym nie istnieje rozbieżność opinii. Sytuacja na rynkach jest dużo bardziej skomplikowana i może generować subiektywność oszacowań, co implikuje niepewność, a więc i rozbieżność opinii. Stąd w ogólnym rozrachunku możemy utożsamiać ryzyko inwestycji z niepewnością.

Załóżmy więc, że przychodzi informacja, że spółka za część wyemitowanego kapitału podejmuje pewną dodatkową inwestycję mającą na celu obniżenie kosztów. Jednak inwestycja ta jest dość ryzykowna. A więc całkowite ryzyko inwestycji wzrasta, ale jednocześnie wywołuje to wzrost rozbieżności opinii. Krzywa ABC zostaje zastąpiona przez FBJ. Jak widać prowadzi to do wzrostu ceny rynkowej z R do Q. Załóżmy następnie, że ta dodatkowa inwestycja udaje się, tak że koszty zostaną rzeczywiście obniżone. To doprowadzi do tego, że część wypłaty pieniędzy w okresie likwidacji staje się bardziej pewna. Ryzyko więc spada, a to prowadzi do spadku rozbieżności opinii. Krzywa FBJ zostaje zastąpiona przez DBE. To jednak prowadzi do spadku wyceny rynkowej, z Q do M. W sytuacji gdy rozbieżność opinii nie występuje - ryzyko jest obiektywne - krzywa popytu staje się linią prostą GBH, a cena spada do G.

Model ten tłumaczy zaobserwowany przez naukowców (np. przez Haugena i Hinesa, a także przez Soldofsky'ego, Millera oraz Pratta) paradoks, że często średnia stopa zwrotu jest ujemnie skorelowana z odchyleniem standardowym. Bardziej ryzykowne walory (to znaczy o wyższym współczynniku beta) przynosiły średnio mniejszy zwrot niż mniej ryzykowne. Jest to oczywiście zjawisko niezgodne z CAPM. Model Millera pokazuje, że staje się to możliwe, gdyż bardziej ryzykowny walor podnosi rozbieżność opinii, a dopóki mniej liczna grupa inwestorów, która optymistycznie ocenia nową inwestycję, w pełni pokryje podaż, wycena rynkowa będzie mogła być odpowiednio wyższa.

No dobrze, ale czy wyższa oczekiwana stopa zwrotu nie podnosi właśnie ceny? Wyższa oczekiwana stopa zwrotu podnosi oczekiwaną cenę E(P(1)) lub obniża P(0). W modelu, który omawiamy występuje zarówno P(0) jak i E(P(1)), jednak wartość E(P(1)) jako wartość oczekiwana pojawia się już w okresie 0. Badanie stóp zwrotu natomiast analizuje dane ex-post, czyli po fakcie - wartość, która się pojawiła się w okresie 0 zaliczona zostaje jako P(0), a wartość w okresie 1 jako P(1). Wartość P(1) jest wartością ex-post dla E(P(1)) - czyli jest to faktyczna wartość, która się pojawiła w okresie 1. Mówiąc krótko - wartość oczekiwana pojawia się szybciej i dlatego staje się wartością bieżącą. A ponieważ wartość bieżąca rośnie, to średnia stopa zwrotu (albo inaczej oczekiwana ex-post stopa zwrotu) spada. Dlatego też - według Millera - badania wykazały ujemną korelację pomiędzy ryzykiem a średnią stopą zwrotu.

Możemy w końcu przejść do sprawy tworzenia się trendu. Jeśli informacje sygnalizujące zwiększenie niepewności będą się często powtarzać, to rozbieżność opinii będzie wzrastać i cena dzięki temu systematycznie wzrasta. Bardziej optymistycznie nastawieni inwestorzy lub też lepiej poinformowani będą traktować informacje jako pozytywną i dopóki wchłoną całą podaż będą "rządzić". Z drugiej strony, jeśli powtarzać się będą informacje sygnalizujące zmniejszenie niepewności, to rozbieżność opinii zacznie spadać i paradoksalnie cena też zacznie spadać. Bardziej optymistyczni i lepiej poinformowani inwestorzy nie będą się zbytnio różnić w ocenach od średniej populacji inwestorów; cena zbliży się do średniej.

Możemy sobie również wyobrazić sytuację, gdy krzywa popytu staje się asymetryczna, tak że górna część staje się silniej nachylona. Mógłby to być typowy przykład z zakresu asymetrii informacji. Pewna niewielka grupa inwestorów wie znacznie więcej od reszty i zaczyna stopniowo, bez hałasu podbijać cenę. Gdy informacja publicznie się ujawnia, cena zwiększa już swoją średnią oczekiwań. Kolejne informacje i kolejne sprzężenia z rozbieżnymi opiniami mogą doprowadzić do utworzenia się trendu.

Oczywiście wszystko zależy od położenia linii podaży N. Jeśli będzie ona przesunięta mocno w prawo w stosunku do krzywej popytu, to popatrzmy co się dzieje - cała analiza się odwraca. Duża liczba inwestorów będzie gorzej od średniej oceniać wartość akcji i każda dodatkowa informacja sygnalizująca wzrost niepewności obniży cenę. Odwrotnie stanie w przypadku informacji zmniejszającej ryzyko. Miller skłania się jednak ku tezie, że liczba inwestorów trzymających wszystkie akcje jest mała w stosunku do całego uniwersum inwestorów, a więc że spełnione są założenia, że to optymiści wyznaczają cenę rynkową. Jednak możemy sobie wyobrazić sytuację, że akcje są tak źle odbierane przez dużą część rynku, że krzywa popytu jest niemal pionowa, a oprócz tego może przecież mieć inny kształt, na przykład im niższa cena, tym mniejsze nachylenie, a nie większe.

Zwróćmy uwagę na fakt, że choć model jest bardzo prosty, bo np. zakłada, że każdy inwestor trzyma jedną akcję, to oczywiście sytuację tę można odpowiednio uogólnić. Każdy inwestor mógłby trzymać n akcji. Wtedy jeśli oś pozioma wyznacza skumulowaną liczbę inwestorów przy danej estymacji, a liczba wszystkich akcji równa się N, to w miejsce N na naszym wykresie wstawiamy N/n. Ponieważ N = M*n, gdzie M - maksymalna liczba inwestorów mogących trzymać wszystkie akcje na rynku, to M = N/n jest liczbą którą musimy wstawić za N.

Na koniec poruszę jeszcze krytykę modelu Millera zapoczątkowaną prawdopodobnie przez Jarrowa (1980). Jarrow zwraca uwagę, że model Millera zakłada heterogeniczność oszacowań oczekiwanej stopy zwrotu oraz homogeniczność oszacowań ryzyka pośród inwestorów. Jeśli inwestorzy oceniają ryzyko na tym samym poziomie, to model Millera może być prawidłowy, a więc rzeczywiście cena będzie rosła wraz ze wzrostem rozbieżności opinii. Jednak rezultat może się zmienić, jeśli ryzyko będzie także niejednorodnie szacowane. Przypomnijmy sobie model Lintnera z poprzedniego artykułu, który opisuje różne sytuacje rozbieżności opinii: zarówno dla oczekiwanej stopy zwrotu, jak i ryzyka. Wprawdzie Lintner nie rozważa w swoim modelu relacji pomiędzy rozbieżnością opinii a ryzykiem/niepewnością, która stanowi klucz do teorii Millera, jednak należy brać pod uwagę wszelkie możliwe przypadki rozbieżnych opinii. Optymiści przewidują wyższe zyski firmy (wyższe dywidendy) bez wzrostu ryzyka. Pesymiści przewidują gorsze wyniki (dywidendy) bez spadku ryzyka. Popatrzmy na wzór:



Jeśli ryzyko się nie zmienia, to jedynie oczekiwana cena E(P1) będzie się zmieniać w zależności od opinii o przyszłych zyskach. Oznacza to, że oczekiwana stopa zwrotu będzie się zmieniać pod wpływem opinii inwestorów o przyszłych zyskach, pomimo że ryzyko (lub opinia o nim) będzie niezmienne. W rzeczywistości jednak ryzyko i awersja do ryzyka może się dodatkowo zmieniać. Widać, że bieżąca cena P(0) będzie tym wyższa, im niższe będzie ryzyko (v) oraz niższa awersja do ryzyka (a).

Jeśli część (av) wzrośnie, wtedy P(0) może spaść. Wtedy oczekiwana stopa zwrotu może wzrosnąć, gdy wzrośnie ryzyko, a nie spaść, jak przewiduje model Millera. Model CAPM zostanie uratowany.


Literatura:

1. E. Miller - Risk, Uncertainty, and Divergence of Opinion, 1977,
2. R. Jarrow - Heterogeneous Expectations, Restrictions on Short Sales, and Equilibrium Asset Prices, 1980,
3. J. Lintner, "The Aggregation of Investor's Diverse Judgments and Preferences in Purely Competetive Security Markets", 1969.

Rozbieżność opinii w kontekście CAPM

Niedawno w poście Teoria portfela nie implikuje efektywnego rynku poruszyłem kwestię rozbieżności opinii na temat wartości akcji wśród inwestorów. Stwierdziłem, że zróżnicowanie oczekiwań sprawia, iż na wartość akcji można spojrzeć jak na przedział liczbowy. Pisałem także, że rozbieżność opinii stanowi jeden z możliwych warunków ukształtowania się trendu cen akcji. W tym artykule obalę mit, że sama rozbieżność opinii wywołuje trend. W tym celu posłużę się publikacją J. Lintnera "The Aggregation of Investor's Diverse Judgments and Preferences in Purely Competetive Security Markets" z 1969 r. podejmującą zagadnienie rozbieżności (niejednorodności) opinii pomiędzy inwestorami. Jest dużo więcej artykułów rozbudowujących tę tematykę, np.
- E. Miller - Risk, Uncertainty, and Divergence of Opinion, 1977
- R. Jarrow - Heterogeneous Expectations, Restrictions on Short Sales, and Equilibrium Asset Prices, 1980,
- C. Chiarella, R. Dieci, X-Z He - Aggregation of heterogeneous beliefs and Asset Pricing Theory: A mean-variance Analysis, 2007

Należy jednak zająć się podstawami.

Lintner w swoim artykule dowodzi, że niejednorodność opinii wśród inwestorów nadal pozwala zachować na rynku optimum Pareta (tzn. sytuację, gdy żadna strona nie jest w stanie poprawić swojej sytuacji bez pogorszenia drugiej strony, a więc rynek pozostaje efektywny), tak że teoria portfela wraz z CAPM może zostać odpowiednio uogólniona. Pomysł polega na zagregowaniu zróżnicowanych opinii inwestorów na temat przyszłej wartości akcji lub ryzyka (wariancji/kowariancji) w pewną uśrednioną opinię, będącą wynikiem sił popytu i podaży. Należy tu zwrócić uwagę, że Lintner zakłada, że obecna cena akcji jest prawidłowa, czyli rynek zachowuje efektywność - inwestorzy zgadzają się, że ich opinie zostaną odpowiednio uśrednione. Powstaje pytanie czy w takiej sytuacji nadal można rozważać wartość akcji przez pryzmat przedziału liczbowego. Można, tyle że musimy tu rozróżnić dwa kryteria: subiektywne i obiektywne. Każdy inwestor wycenia w ramach swoich możliwości jak najbardziej obiektywnie akcje. Zawsze jednak jego wycena będzie zawierać pewną dozę subiektywizmu. I to jest kryterium subiektywne. Rynek uśrednia wyceny wszystkich inwestorów w rynkową wycenę akcji. To jest kryterium obiektywne. Z punktu widzenia kryterium subiektywnego wartość akcji stanowi pewien przedział liczbowy. Z punktu widzenia kryterium obiektywnego wartość akcji stanowi konkretną liczbę, a subiektywna wycena jakiegoś inwestora jest po prostu losowym zakłóceniem prawidłowej wyceny.

Rozważając subiektywne wyceny, możemy stwierdzić, że inwestorzy posiadający identyczne preferencje ryzyka, będą trzymali akcje w portfelu w różnych proporcjach. Każdy z nich będzie stosował teorię portfela, ale może uzyskać inny skład portfela. Czyli mapa ryzyko-oczekiwana stopa zwrotu w teorii portfela będzie się przesuwać i zmieniać kształt w zależności od inwestora. Będzie również istnieć "rynkowa" mapa ryzyka i oczekiwanej stopy zwrotu, uśredniająca subiektywne mapy.

Należy zwrócić również uwagę, że decyzje inwestorów o skrajnie subiektywnych wycenach nie są błędne. Jeśli nazywać je już tak, to najwyżej można byłoby powiedzieć, że są to "wymuszone błędy".

Zakładamy dwa okresy: 0 i 1. Jest N walorów indeksowanych literką i oraz j. Jest także M inwestorów indeksowanych literką k. Lintner najpierw wyprowadza następujący wzór na oczekiwaną cenę akcji i-tego waloru k-tego inwestora w okresie 1:



Jeśli chodzi o v(i,k) to jest to jakby krańcowa wariancja portfela do i-tego waloru dla k-tego inwestora. Nie musimy tutaj się wgłębiać w znaczenie tej miary - najważniejsze, żeby zobaczyć, że jest proporcjonalna do kowariancji dla walorów i,j dla k-tego inwestora.

Można łatwo pokazać, że uśredniona (dla wszystkich inwestorów) oczekiwana cena akcji w okresie 1 jest równa:

Jeśli podzielimy obie strony przez P(0) i odejmiemy 1 z obu stron, to dostaniemy wzór na uśrednioną dla wszystkich M inwestorów oczekiwaną stopę wzrostu ceny i-tego waloru:

Załóżmy dla uproszczenia, że spółki nie wypłacają dywidend w okresie 1. Wówczas g(i) jest to oczekiwana stopa zwrotu i-tego waloru, co oznacza, że możemy to równanie potraktować jak uogólniony CAPM-SML dla rozbieżnych opinii. Model ten zapisywaliśmy w postaci:



W takim razie (uśredniona) i-ta cena ryzyka jest zależna od (uśrednionej) awersji do ryzyka oraz kowariancji cen i,j:

Wnioski są interesujące. Powyższy wzór jest na tyle ogólny, iż możemy stwierdzić, że nawet jeśli wszyscy inwestorzy mają takie same oczekiwania i opinie co do i-tej oczekiwanej stopy zwrotu, to i-ta cena ryzyka będzie zależeć nie tylko od kowariancji, ale także od awersji do ryzyka. A przecież awersja do ryzyka należy do dziedziny preferencji danego inwestora.

Załóżmy najpierw, że wszyscy mają identyczne oszacowania przyszłej ceny akcji (czyli także oczekiwanej stopy zwrotu) oraz ryzyka (wariancji/kowariancji cen, ale także stopy zwrotu). W takiej sytuacji, jeśli ktoś będzie miał wyższą awersję do ryzyka, to po prostu oczekiwana stopa zwrotu będzie musiała być mniejsza (inwestor chce mniej ryzykować). Ale ponieważ przyszła oczekiwana cena zależy dodatnio od awersji do ryzyka, to wariancja portfela będzie musiała odpowiednio mocniej spaść. Dostajemy więc klasyczny model - jeśli inwestor chce więcej (mniej) ryzykować, to posiada większe (mniejsze) ryzyko inwestycji, a wtedy oczekiwana stopa zwrotu rośnie (maleje).

Następnie uogólnimy ten przypadek. Załóżmy jeszcze raz, że wszyscy zgadzają się co do przyszłej ceny i-tej akcji. O ile aktualna cena akcji jest znana, to znów trzeba się zastanowić nad pozostałymi wyrazami: awersją do ryzyka i wariancją. Aby oczekiwana cena pozostała stała, to inwestorzy NIE MUSZĄ zgadzać się co do oszacowania wariancji, czyli ryzyka. Jeśli inwestor 1 uważa, że ryzyko jest wyższe niż inwestor 2, to aby ich oczekiwana cena pozostała identyczna, muszą się różnić awersją do ryzyka. Awersja do ryzyka inwestora 1 musi wtedy odpowiednio (stosunkowo) spaść.

Może się zdarzyć także sytuacja odwrotna. Inwestorzy mogą zgadzać się co do ryzyka, ale już nie oczekiwanej przyszłej ceny. Wówczas jeśli inwestor 1 ma wyższe oczekiwania ceny niż inwestor 2, to aby oszacowania ryzyka pozostały identyczne, awersja do ryzyka inwestora 1 musi stosunkowo wzrosnąć.

Inwestorzy mogą w końcu różnić się w ocenach zarówno przyszłej ceny, jak i ryzyka. W takiej sytuacji awersja do ryzyka przestaje mieć znaczenie "stabilizatora", bo każdy może mieć dowolne równanie oczekiwanej ceny. Stąd także każdy będzie posiadał swoje własne oszacowania SML. Oczywiście będzie podążał za racjonalnymi oczekiwaniami, lecz subiektywizmu w praktyce nie uda mu się ominąć. Oszacowania przyszłej oczekiwanej stopy zwrotu na podstawie średnich w przeszłości to duże uproszczenie zakładające, że przyszłość będzie taka jak przeszłość. Jednakże często to założenie nie jest uprawnione. Wykorzystywanie nowych, aktualnych informacji w sporządzaniu SML i wyceny dyskontowej rodzi duże pole do rozbieżności opinii. Dopiero rynek uśrednia wszystkie te opinie losując "obiektywną" wartość rynkową. Trochę to śmiesznie brzmi: rynek losuje wartość, którą należy uznać za obiektywną. Ale trzeba też pamiętać, że nie uwzględniamy tutaj różnych nieefektywności rynku, jak np. asymetria informacji czy też ataki spekulantów mające na celu wywołanie paniki lub euforii. Tak więc na razie kwestię formowania się trendów pozostawiam na boku. Dowodzę tylko, że sama rozbieżność opinii nie może stanowić przesłanki do tego, że kurs ma tendencję do poruszania się w danym kierunku.

Literatura:

J. Lintner, "The Aggregation of Investor's Diverse Judgments and Preferences in Purely Competetive Security Markets", 1969.