Z kolei niepewność to termin dość mglisty, bo niedookreślony. Zazwyczaj łączy się go z nieznanym rozkładem prawdopodobieństwa stopy zwrotu lub wskaźników finansowych. W tym miejscu powstaje wiele nieporozumień, bo trzeba dokładnie zdefiniować co rozumiemy przez niepewność, które dla inwestorów stało się słowem-wytrychem. Jeśli mówimy o niepewności stopy zwrotu, to musimy określić czy nieznana jest oczekiwana stopa stopa zwrotu czy nieznane jest ryzyko (odchylenie standardowe). Jednakże niepewność może też dotyczyć strony czysto fundamentalnej, jak np. rentowności kapitału własnego, tj. ROE. Wtedy musimy określić czy nieznane jest średnie ROE czy zmienność ROE.
Możemy więc wyróżnić 4 podstawowe przypadki wpływu parametrów na wartość akcji:
- od strony stopy zwrotu (przy innych czynnikach niezmienionych):
1. wzrost (spadek) oczekiwanej stopy zwrotu (stopy dyskontowej) -> spadek (wzrost) wartości akcji
2. wzrost (spadek) odchylenia standardowego (ryzyka) -> spadek (wzrost) wartości akcji
- od strony ROE (przy innych czynnikach niezmienionych):
3. wzrost (spadek) oczekiwanego ROE -> wzrost (spadek) wartości akcji
4. wzrost (spadek) odchylenia standardowego ROE -> ???
Z tego wynika, że tylko wzrost lub spadek zmienności ROE ma niejasny wpływ na wartość akcji. Intuicyjnie może się wydawać, że wzrost zmienności ROE oznacza to samo co wzrost ryzyka stopy zwrotu, czyli spadek wartości akcji (przy ceteris paribus). Tyle że na intuicji nie zawsze można polegać.
L. Pastor i P. Veronesi w [1] wskazują, że dopóki zmienność ROE wynika z niesystematycznych, czyli nierynkowych przesłanek, wzrost (spadek) tej zmienności przynosi wzrost (spadek) wartości akcji. Wiadomo bowiem, że ROE składa się z dwóch części: systematycznej (czyli samej oczekiwanej stopy zwrotu) i niesystematycznej (czyli specyficznej dla danej spółki). Jeśli część niesystematyczna jest większa (mniejsza) od 0, to wartość akcji (P) jest większa (mniejsza) od wartości kapitału własnego na akcję (BV). Część niesystematyczna może składać się z premii za zmienność innowacyjnych przedsięwzięć. Nie chodzi tu tylko o premię za ryzyko niepowodzeń takich inwestycji, lecz także o fakt, że innowacje niosą ryzyko chwiejności wzrostu zysku - niektóre innowacje mogą przynosić większe, a inne mniejsze zyski. W każdym razie specyfika innowacji jest zupełnie niezależna od zachowania rynku jako całości. Oznacza to, że gdy rośnie ryzyko samych innowacji, stopa dyskontowa nie zmienia się.
Załóżmy, że spółka A zainwestowała w innowacje i generuje z niej zyski, a więc część niesystematyczna ROE jest większa od 0, co implikuje P(0) > BV(0). (Ponadto do okresu 0 do T spółka nie wypłaca dywidend). Jednakże w pewnym okresie T część niesystematyczna spada do 0, czyli spółka nie jest już w stanie generować innowacji, "premia za ryzyko innowacji" spada do 0, a więc P(T) = BV(T). Uzasadnić to można w ten sposób, że konkurencja rozwija własne pomysły, eliminując tym samym zyski nadzwyczajne firmy A. Od okresu 0 do T, BV(t) rośnie w pewnym stałym tempie g. Wartość g można potraktować jako wartość oczekiwaną stopy wzrostu, gdyż w rzeczywistości stopa wzrostu podlega różnym wahaniom, czyli jest zmienną losową. W okresie T BV(T) wynosi:
Ponieważ wzrost BV(t) jest średnio stały w czasie, nic nie stoi na przeszkodzie, by potraktować go jako proces ciągły w czasie. Najpierw każdy okres t podzielimy na n podokresów i każdy podokres będzie kapitalizowany. Stopę procentową g podzielimy także na n, po to aby otrzymać tempo wzrostu w danym podokresie. (Będzie to prawidłowe pod warunkiem, że g będzie logarytmiczną stopą wzrostu - to z kolei nie jest niczym nadzwyczajnym, gdyż pojęcie stóp procentowych jakie znamy odnosi się właśnie do logarytmicznych a nie arytmetycznych stóp wzrostu w celu umożliwienia szybkiego obliczania kapitalizacji półrocznej, kwartalnej, miesięcznej itd):
Jeśli liczba podokresów n dąży do nieskończoności:
to możemy skorzystać ze znanego wzoru:
I w ten sposób przechodzimy z kapitalizacji nieciągłej na ciągłą:
Choć g potraktowaliśmy jako wartość oczekiwaną tempa wzrostu, to w rzeczywistości wartość ta nie jest znana, czyli również jest zmienną losową. Od okresu 0 do T została "wylosowana" pewna wartość g. Możemy w uproszczeniu uznać g za zmienną o rozkładzie normalnym z wartością oczekiwaną G i wariancją σ^2. Czyli BV(T) staje się wartością oczekiwaną:
Ale jeśli g ma rozkład normalny, to exp(g) ma rozkład logarytmiczno-normalny . Z kolei wartość oczekiwana zmiennej o rozkładzie logarytmiczno-normalnym jest dana wzorem [2],[3]:
Czyli dostaniemy:
Zauważmy teraz, że jeśli zdyskontujemy wartość BV(T) T okresów za pomocą stopy dyskontowej r, to uzyskamy P(0). Wykorzystując analogiczne przekształcenia przejścia od kapitalizacji nieciągłej do ciągłej dla stopy dyskontowej, uzyskujemy wzór na wartość akcji P(0):
Możemy również przedstawić wskaźnik P/BV w następującej postaci:
Zwróćmy uwagę, że gdy wzrasta odchylenie standardowe g, to wzrasta P/BV. Co ciekawe, wtedy BV nie zmienia się. Ponieważ g stanowi nie tyle wartość oczekiwaną co zmienną losową (wartości oczekiwanej) tempa wzrostu o pewnych parametrach, to mówiąc o odchyleniu standardowym g jesteśmy już blisko tego co nazywamy właśnie "niepewnością". A więc możemy powiedzieć, że gdy rośnie niepewność zysków nadzwyczajnych (nadwyżkowych monopolistycznych), wzrasta wartość fundamentalna akcji, a wartość księgowa nie zmienia się.
Aby zrozumieć jaki mechanizm tutaj działa, zilustrujemy go następującym przykładem podanym przez Pastora i Veronesiego. Załóżmy, że firmy A i B różnią się tylko przyszłym tempem wzrostu ich wartości księgowej, której bieżąca wartość wynosi 1 mln zł. Gdy A zamierza wzrastać 10% na rok z prawdopodobieństwem 1, B wzrasta albo w tempie 5%, albo 15% na rok z równym prawdopodobieństwem. I tak w ciągu 10 lat 1 mln zł kumuluje się do 4,05 mln zł przy 15%, do 2,59 mln zł przy 10% i do 1,63 mln zł przy 5%. Wtedy firma B ma wyższą oczekiwaną przyszłą wartość księgową niż A, bo (4,05 + 1,63) / 2 = 2,84 > 2,59.
Należy tu ciągle pamiętać, że stopa dyskontowa r wyrażająca premię za ryzyko systematyczne pozostaje stała, bo zyski monopolistyczne-nadwyżkowe nie korelują z zyskami konkurencji rynkowej. Należy zauważyć, że g to nie jest nadwyżkowa stopa wzrostu, lecz całkowita. To oznacza, że niepewność σ^2 zawiera częściowo zarówno ryzyko systematyczne jak i niesystematyczne. Należy więc tutaj rozróżnić dwie sytuacje.
Po pierwsze może wzrosnąć (spaść) tylko ryzyko systematyczne. Wpływ tego zdarzenia na P/BV wymaga oddzielnego komentarza i zastanowienia. Po drugie może wzrosnąć tylko ryzyko niesystematyczne (specyficzne). Ten przypadek został powyżej dokładnie omówiony.
Jak pamiętamy g ściśle wiąże się z ROE. Ponieważ g oznacza dokładnie stopę wzrostu wartości księgowej, a nie zysku, to znaczy, że g = k*ROE, gdzie
k - część zysku netto z okresu bieżącego zwiększająca kapitał własny z okresu poprzedniego..
Przypomnijmy może skąd ten wzór wynika:
BV(t) = BV(t-1) + k*ZYSK(t) = BV(t-1)*(1+k*ZYSK(t) / BV(t-1)) = BV(t-1)*(1 + k*ROE) = BV(t-1)*(1 + g) => g = k*ROE.
Zmienność g będzie ściśle związana ze zmiennością ROE. Ale ponieważ g charakteryzuje się też niepewnością, to i ROE charakteryzuje się niepewnością. Ogólnie stwierdzamy, że zmienność czy niepewność o średniej ROE zwiększa P/BV.
Jednak błędem jest twierdzenie, że większa zmienność ROE zwiększa P/BV. Wcześniej zostało wskazane, że nie może to być ryzyko systematyczne. Dopiero wzrost ryzyka niesystematycznego wpłynie dodatnio. Zmiany średniej ROE mamy z kolei prawo uznać jako nieskorelowane z ryzykiem systematycznym.
Powyższa analiza stanowi jedynie wstęp do rozbudowanego modelu Pastora i Veronesiego, którzy dalej wprowadzają model, w którym rynek uczy się, czego należy się spodziewać po spółce. Z pomocą przychodzi wtedy warunkowa zmienna losowa, której parametry są zależne od przeszłych wartości. Prowadzi to do wniosku, że największa warunkowa niepewność (średniego) ROE występuje w początkowych fazach życia firmy, co prowadzi do wyższego P/BV w tym okresie (a więc w późniejszej fazie życia P/BV staje się niższy). Ponadto Autorzy rozróżniają sytuacje, gdy spółka wypłaca i nie wypłaca dywidend. Model zgodnie z intuicją wskazuje, że większa niepewność występuje w przypadku firm niepłacących dywidend, a więc te powinny mieć wyższe P/BV. Autorzy stawiają też sugestię, że duże wartości P/BV wielu spółek z giełdy w USA pod koniec lat 90-tych mogły wynikać z tej większej niepewności, zamiast braku racjonalności rynku.
Przykładowo poniższy wykres obrazuje modelową zależność pomiędzy niepewnością o średniej ROE (oś pozioma) a wskaźnikiem P/BV (oś pionowa):
Literka c oznacza część wartości księgowej (BV), którą spółka wypłaca akcjonariuszom w postaci dywidendy. Widać, że im mniejsza dywidenda, tym większe P/BV.
W końcu również empirycznie dowodzą oni swoich tez, wykorzystując regresję liniową. Do badania użyli rocznych danych od 1962 do 2000 r. z CRSP/Compustat database. Zbudowana regresja w dużym stopniu potwierdziła przewidywania modelu teoretycznego.
Literatura:
[1] Pastor, L., and P. Veronesi. "Stock Valuation and Learning about Profitability." Journal of Finance, 58 (2003), 1749-1789;
[2] http://en.wikipedia.org/wiki/Log-normal_distribution;
[3] Ossowski, J. C., "Rozkład logarytmiczno-normalny a względne i absolutne miary rozproszenia", Toruń 2003.




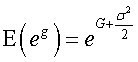




Brak komentarzy:
Prześlij komentarz