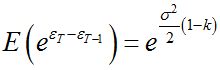Problem estymacji parametrów nieliniowych funkcji losowych poprzez
przekształcenia liniowe jest znany w statystyce od dawna i ma bogatą
historię. Zajmowali się nią Barlett [1], Quenouille [2], Neyman i Scott
[3], Box i Cox [4], Hoyle [5], Granger i Newbold [6], Duan et al. [7],
Taylor [8] i wielu innych. W szczególności transformacjami rozkładów
lognormalnych zajmowali się Finney [9], Mostafa i Mahmoud [10],
Meulenberg [11], Goldberger [12], Bradu i Mundlak [13] , Heien [14], Teekens
oraz Koerts [15], Evans i Shaban [16], Duan [17].
Zacznijmy ponownie od modelu, który opisałem w
Czy mediana jest lepsza od średniej?, tj. proces geometrycznego ruchu Browna, jednak dla uproszczenia pomińmy stałą, która nie ma tutaj wpływu na analizę:
(1)
Logarytmując
model (1) uzyskujemy funkcję liniową, co pozwala nam na użycie MNK:
Wiemy
już, że prosta delogarytmizacja ostatniego równania nie prowadzi do
otrzymania wartości oczekiwanej P(t). Aby ją uzyskać, musimy wykorzystać
własności rozkładu lognormalnego. Składnik losowy z początkowego
założenia ma rozkład normalny, wobec czego exp(składnik losowy) ma
rozkład lognormalny. Ale co z parametrem b? Dotychczas dla uproszczenia
zakładaliśmy, że b jest znane. W rzeczywistości nie znamy parametru b. Jeżeli nawet b jest nieznane, to ciągle pozostaje stałą, wobec czego wartość oczekiwana zmiennej lognormalnej pozostaje jak w poprzednich rozważaniach:
(2)

W
rzeczywistości b jest nieznane, bo operujemy zawsze na pewnej próbie
losowej, a więc
szacowany parametr będzie się zachowywał jak zmienna losowa (dla danego okresu) o
pewnej wartości oczekiwanej i wariancji. Trzeba zauważyć, że w
ekonometrii mamy 2 rodzaje wartości oczekiwanych:
dla stałej wartości (w populacji) oraz dla zmiennej losowej (w
populacji i w próbie). W pierwszym przypadku mamy do czynienia po prostu
z prawdziwym parametrem istniejącym de facto dla pełnej populacji.
Jednak próbki z tej populacji będą losowe i będą kreować statystyki, jak
średnia i wariancja. Dopiero przy bardzo dużej liczebności próbki,
wariancja będzie spadać do zera, tak że pozostanie tylko średnia, która
zbliży się do prawdziwego parametru i w ten sposób wartość oczekiwana
zmiennego parametru z próby będzie się równać prawdziwemu (stałemu) parametrowi. W
drugim przypadku wartość oczekiwana dotyczy zmiennej losowej niezależnie czy myślimy o próbie czy populacji. Wtedy próbki losowe będą kreować
własne rozkłady, ale wraz z wielkością próby będą zbliżać się do
rozkładu z populacji, podobnie jak w pierwszym przypadku. Jednakże tym razem
wariancja nie będzie już spadać do zera wraz z liczebnością próby.
Niezależnie
od tego czy mówimy o pierwszym czy o drugim przypadku, zawsze określenie
"wartość oczekiwana" będzie się odnosić do średniej z populacji.
Wartość oczekiwana parametru b będzie więc równać się prawdziwemu
parametrowi.
Przyjmiemy pierwszy przypadek. Chociaż
moglibyśmy przyjąć drugą możliwość - z parametrem jako zmienną losową -
to czyniłoby to analizę znacznie bardziej skomplikowaną. Dlatego przyjmiemy
standardowy punkt widzenia - czyli że istnieje tylko jeden prawdziwy
parametr, ale dążymy do jego uzyskania na podstawie prób losowych.
Oznacza to, że parametr b jest stały, więc model (2) jest nadal
poprawny.
Formalnie rzecz biorąc model (1) stanowi model dla całej populacji. Stąd również model (2) dotyczy całej populacji. Jeżeli więc tworzymy model w oparciu o próbę losową, to nasze parametry zaczynają już się wahać, stają się zmiennymi losowymi, a przez to, aby zachować formalność, musimy te zmienne jakoś inaczej oznaczyć, aby odróżnić je od prawdziwych (stałych) parametrów. Oznaczymy je daszkiem. Uzyskamy więc na podstawie próby losowej cenę z daszkiem, parametr b z daszkiem, a nawet składnik losowy z daszkiem, bo ogólnie rzecz biorąc może on się inaczej zachowywać niż prawdziwy składnik losowy z populacji. Mówiąc krótko, estymujemy model (1) za pomocą:
(3)
Ponieważ składnik
losowy ma rozkład normalny, to zmienna b także. Naszym zadaniem jest teraz znaleźć wartość oczekiwaną ceny z daszkiem. Pamiętajmy jednak czym jest cena z daszkiem - to losowa prognoza ceny. Zatem szukamy oczekiwanej prognozy ceny. Zmienna b z daszkiem jest ciągle zmienną losową o
rozkładzie normalnym, zatem exp(bt) ma rozkład log-normalny, czyli cena z daszkiem ma rozkład log-normalny. A więc szukamy wartości oczekiwanej zmiennej o takim rozkładzie. Wzór na nią jest znany. Wzór ten zawiera w sobie wartość oczekiwaną b z daszkiem oraz wariancję b z daszkiem. W naszym wypadku zakładamy, że wariancja współczynnika b jest znana, tzn. jest równa wariancji współczynnika b z daszkiem. Z własności wartości
oczekiwanej i wariancji wiemy, że
, ponieważ czas t jest oczywiście stałą.
Całkowity model z wartością oczekiwaną to
przekształcenie z (3)
(4)
Zwróćmy uwagę, że wariancja składnika losowego jest funkcją czasu, a nie stałą - w każdym kolejnym okresie się zwiększa.
Aby
nie mylić jednostek czasowych ze zmienną, t zastąpimy ostatnim okresem
T. Ponieważ wariancja składnika losowego sumuje się w czasie, zapiszemy ją jako średnią
wariancję przemnożoną przez T:
(5)
Aby
uprościć model (5), wykorzystamy dwa znane wzory: na ocenę
parametru b z daszkiem oraz wariancję parametru b z daszkiem. (Oba można znaleźć np. w Uriel
[18], wzory 2-37 + 2-64). Pierwszy to estymator MNK dla b, który oznaczymy jako b z falką, w sytuacji gdy
stała w modelu liniowym jest równa 0:
(6)
Jednak
sumę kwadratów liczb naturalnych można wyrazić za pomocą (zob. np.
http://www.trans4mind.com/personal_development/mathematics/series/sumNaturalSquares.htm):
(7)
Stąd:
(8)
Drugi wzór - na wariancję współczynnika b pokażemy od razu wykorzystując wzór (7):
(9)
Wariancja ta nie zawiera już falki, bo z początkowego założenia była znana. Ponieważ wariancja składnika losowego jest znana, to podstawiamy (9) do (5):
(10)
Uzyskaliśmy ocenę wartości oczekiwanej ceny. W końcu przypomnijmy, że (2) można zapisać:
(11)
Co oznacza, że nasz model (10) będzie go przypominał wraz ze wzrostem liczebności próby T:
Inaczej mówiąc:
Ale tak będzie tylko w przypadku, gdy T jest duże. Trzeba w tym miejscu mocno uświadomić sobie co to oznacza. Model (10) jest wartością oczekiwaną prognozy ceny (prognoza ceny jest zmienną losową).
Oczekiwana prognoza ceny jest pewną średnią opartą na obserwacjach historycznych. Tymczasem model (11) jest wartością oczekiwaną samej ceny. Dopiero w długim okresie model (10) zrówna się z modelem (11). Tak nakreślona sytuacja pozwala nam określić kryterium, za pomocą którego wybierzemy jedną z tych dwóch wartości oczekiwanych. Czy chcemy odnaleźć wartość oczekiwaną z próby losowej czy wartość oczekiwaną z populacji. Wcześniej jednak stwierdziłem, że mówiąc o wartości oczekiwanej mam na myśli zawsze średnią w populacji, jeśli więc dotyczy próby, to nie jest to wartość oczekiwana. Wynika z tego, że model (10) jest
estymatorem obciążonym wartości oczekiwanej ceny. Nie jest wcale oczywiste, że obciążony estymator należy odrzucić. Ważniejsza jest efektywność estymatora. W tym przypadku mniejszą wariancję posiada jednak
estymator nieobciążony wartości oczekiwanej ceny - model (11), który nas interesuje (widać, że w modelu (10) współczynnik f jest dodatni, więc powiększa wariancję, więc jest gorszy). Problem leży w wyłuskaniu jego empirycznej postaci.
Problem ten rozwiązuje Meulenberg [11]. Zauważa on, że model (10) jest modelem empirycznym, a więc to on będzie punktem zaczepienia. Pomiędzy modelem (10) a (11) istnieje pewna relacja. Na początku przecież stwierdziłem, że wartość oczekiwana zmiennej b z daszkiem będzie równa b, czyli:
(12)
Ale wtedy dla dowolnego T można będzie (10) zapisać:
(13)
A wtedy (13) można przekształcić:
I w ten sposób dostajemy równanie na poszukiwaną E(P):
(14)
Co wstawić za E(P z daszkiem)? Meulenberg stwierdził, że (10), a więc także (13) jest modelem empirycznym, a więc już zawierającym parametry obliczone MNK. Zauważmy jednak do czego to prowadzi. Jest to najtrudniejszy moment w teorii, więc powtórzmy. Zaczynamy od modelu (3), logarytmujemy i z liniowego modelu wyznaczamy poprzez MNK empiryczne b, które oznaczamy jako b z falką. Ale b z falką jest stałą (w przeciwieństwie do b z daszkiem), a nie zmienną losową. Jeżeli więc teraz podstawimy tę stałą do modelu liniowego, to retransformacja do modelu wykładniczego (3) i wyznaczenie wartości oczekiwanej wykładniczego modelu (3) nie będzie zawierać składnika f, związanego z wahaniami estymacji. Zatem wartość oczekiwana z (3)
stanie się prostym modelem:
(15)
Pomysł Meulenberga polega na zrównaniu modelu (13) z modelem (15). Później przeanalizujemy czy jest on trafny.
(16)
Przekształcając:
Co daje:
(17)
Stąd:
(18)
Czyli:
(19)
Lub w nieco prostszym ujęciu:
(20)
Model (20) jest tym, czego szukaliśmy: zawiera wszystkie składniki gotowe do użycia w regresji liniowej MNK. Pozostaje jeszcze kwestia wariancji. Do jej estymacji może służyć zwykła wariancja logarytmicznej stopy zwrotu, ale formalnie należy użyć tzw. błędu standardowego
reszt, będącego pierwiastkiem wariancji składnika resztowego (formalność wynika z ciągłości użytej funkcji).
Podobnie
jak to wcześniej analizowaliśmy, gdy T rośnie, błędy związane z
przekształceniem
funkcji liniowej w wykładniczą tracą coraz bardziej na znaczeniu, tak że
w dużej próbie b z falką stanie się bliskie prawdziwemu parametrowi b (a więc k spada do zera).
Teraz przeanalizujemy trochę dokładniej sposób Meulenberga, ponieważ wcale nie jest jasne utożsamienie (13) z (15). Wróćmy jeszcze raz do tej równowagi w (16) i przekształćmy inaczej:
(21)
W końcu, biorąc pod uwagę zapis (20) trzeba zauważyć, że (21) można zapisać:
(22)
Zwróćmy uwagę na (22):
odejmuje się tu pewną zawyżoną część wariancji, aby zrównać ocenę parametru z prawdziwym parametrem b.
Warto jeszcze raz odróżnić ocenę wartości oczekiwanej od tej wartości:
Zazwyczaj mniej lub bardziej świadomie popełnia się ten błąd, że prawdziwy parametr b jest równy ocenie tego parametru, czyli b z falką. Formalnie rzecz biorąc nie można więc podstawić b z falką ani do modelu (2) ani (10). Podstawienie b z falką do (16) wynika wyłącznie ze stwierdzenia, że b z falką już zawiera w sobie zawyżoną kapitalizację wskazując tym samym na jej pochodzenie od zmiennej losowej. Prosto mówiąc: wiem, że (13) jest zawyżone oraz wiem, że (15) jest zawyżone, ale też wiem, że obydwa pochodzą od tego samego modelu (3) - wobec tego
zakładam, że mogę je ze sobą zrównać. Oto wyjaśnienie zapisu (16), który wydaje się teraz sensowny.
Ostatecznie widać jaki błąd wywołuje retransformacja z modelu liniowego do nieliniowego:
błąd
ten bierze się stąd, że ocena parametru b ulega procentowym zmianom w czasie, jest
zmienną losową, natomiast prawdziwy parametr jest stały w czasie. Gdyby
ocena była stałą liczbą, błąd ten nie wystąpiłby.
Faktycznie, nie jest to prosty temat. Przyda się przykład.
Przykład.
Na podstawie wzoru (20) nie trudno zauważyć, że duża liczebność obserwacji sprawia, że błędy retransformacji nie mają praktycznie żadnego znaczenia. Dlatego najlepszym sprawdzianem będzie niewielka próbka. Weźmy roczne dane mbanku od końca 1994 do końca 2015 r. i są to 22 obserwacje.
Statystyki stopy zwrotu:
średnia = 20,08%
mediana = 12%
średnia geometryczna = 11,71%
odch. standardowe = 45,5%
Tworzymy model (1):
Logarytmujemy:
Uzyskujemy:
Obliczamy parametr regresji b w KMNK. Uzyskałem 11,18%. Błąd standardowy reszt (tj. odchylenie standardowe składnika losowego) wyniósł 34,6%. Następnie stosujemy (20) dla oczekiwanej stopy zwrotu:
gdzie R to stopa zwrotu jako zmienna losowa.
Podstawiamy:
Porównajmy wynik ze standardowym wzorem dla k = 0:
Błąd retransformacji wynosi 0.04%.
Dwie uwagi. Po pierwsze warto zauważyć jak należy używać wariancji. Wariancja składnika losowego liczona jest jako
suma kwadratów składnika losowego podzielona przez liczbę obserwacji
(22) pomniejszoną o liczbę stopni swobody (2). Nie jest to więc zwykła
wariancja, gdyż dotyczy modelu liniowego. Nie jest to też zwykła wariancja
logarytmicznych stóp zwrotu.
Po drugie zwróćmy uwagę, że użyłem modelu ze stałą. Model empiryczny tego wymaga, gdyż bez stałej zakładamy, że jest ona równa zero, czyli, że P(0) = 1. To spowodowałoby błędne nachylenie linii regresji. Trzeba jednak pamiętać, że wzór (7) zakładał właśnie brak stałej. Dlaczego więc można stosować ciągle wzór (20)? Oczywiście dlatego, że interesuje nas stopa zwrotu brutto M, czyli stopa netto R. A ta rzecz jasna nie może zależeć od poziomu stałej.
Literatura:
[1] M. S. Bartlett, The Use of Transformations, Mar 1947
[2] M. H. Quenouille, Notes on Bias in Estimation, Dec 1956
[3] J. Neyman, E. L. Scott, Correction for Bias Introduced by a Transformation of Variables, Sep 1960
[4] G. E. P. Box, D. R. Cox, An Analysis of Transformations, 1964
[5] M. H. Hoyle, Estimating Generating Functions, Nov 1975
[6] C. W. J. Granger, P. Newbold, Forecasting Transformed Series, 1976
[7] N. Duan, W. G. Manning, Jr., C. N. Morris, J. P. Newhouse, A
Comparison of Alternative Models for the Demand for Medical Care, Apr
1983
[8] J. M. G. Taylor, The Retransformed Mean After a Fitted Power Transformation, Mar 1986
[9] D. J. Finney, On the Distribution of a Variate Whose Logarithm is Normally Distributed, 1941
[10] M. D. Mostafa, M. W. Mahmoud, On the Problem of Estimation for the Bivariate Lognormal Distribution, Dec 1964
[11] M. T. G. Meulenberg, On the Estimation of an Exponential Function, Oct 1965
[12] A. S. Goldberger, The Interpretation and Estimation of Cobb-Douglas Functions, 1968
[13] D. Bradu and Y. Mundlak, Estimation in Lognormal Linear Models, Mar 1970
[14] D. M. Heien, A Note on Log-Linear Regression, 1968
[15] R. Teekens, J. Koerts, Some Statistical Implications of the Log Transformation of Multiplicative Models, Sep 1972
[16] I. G. Evans, S. A. Shaban, A Note on Estimation in Lognormal Models, Sep 1974
[17] N. Duan, Smearing Estimate: A Nonparametric Retransformation Method, Sep. 1983
[18] E. Uriel, The simple regression model: estimation and properties, 09-2013
http://www.trans4mind.com/personal_development/mathematics/series/sumNaturalSquares.htm