Poprawka do wyceny Orlenu: spadnie poniżej 60?

W obliczu mocnej wyprzedaży Orlenu w ostatnich tygodniach zdecydowałem, że należy dokładniej przeanalizować niektóre parametry do mojej wyceny tej spółki. Wycena mieściła się w zakresie od 70 do 75, ale przy obniżaniu stóp nawet do niemal 100 zł.

Kluczowym założeniem było przyjęcie minimalnej oczekiwanej stopy zwrotu na poziomie 9,2% jako sumy stopy wolnej od ryzyka i minimalnej premii za ryzyko. 

Aby ocenić poprawność tego założenia, pomyślmy w ten sposób. Mamy wartość oczekiwaną:

(1) W = p*0 + (1-p)*x

gdzie

W - wartość oczekiwana minimalnej stopy zwrotu

p - prawdopodobieństwo utraty zysku lub straty

x - procentowy zysk (stopa zwrotu)

Wychodzimy od długoterminowej obligacji skarbowej, tzn. p = 0 i x = 7%:

W = 0*0 + (1-0)*7% = 7%

Ile wynosi p dla obligacji korporacyjnej? Aby to ocenić, skorzystam z pracy [1], w której szacowano ryzyko bankructwa wśród przedsiębiorstw przemysłowych sporządzających sprawozdania finansowe w latach 2005-2009. Sporządzono dwie wersje: analiza dla sprawozdań na rok przed bankructwem oraz na dwa lata przed bankructwem. Baza zawierała 133 (7,2%) bankrutów i 1719 (92,8%) przedsiębiorstw zdrowych.

Na pierwszy rzut oka z punktu widzenia samej częstości, prawdopodobieństwo "obiektywne", niewarunkowe upadłości, wyniosło ok. 0,07. Jednakże taki wniosek byłby uprawniony tylko wtedy gdyby to badanie dotyczyło tego jednego roku lub dwóch przed upadłością. Obejmowało ono jednak kilka lat, zatem niektóre bankruty w początkowych latach nie były jeszcze nimi. Dlatego w zależności od wersji badania, całkowita liczba niebankrutów wzrośnie. Liczba bankrutów także wzrośnie ze względu na nakładające się lata przy badaniu wersji dwuletniego wyprzedzenia bankructwa (jeżeli w pierwszym roku wychodził bankrut, to zapewne w następnym roku też wychodził z tego samego bankrut, jeszcze przed faktycznym bankructwem). Inaczej mówiąc czas jest traktowany tu jak przestrzeń, więc każdy  nowy rok (kolejne dwa lata w wersji drugiej) jest traktowany jak dodatkowa baza danych. W sumie baza zawierała 7329 rekordów. w tym 

- 182 bankrutów (2,5%) i 

- 7147 nie-bakrutów (97,5%).

Kierując się tą uproszczoną statystyką, dostalibyśmy prawdopodobieństwo zaledwie 0,025, że spółka nie spłaci zobowiązań wobec obligatariuszy. Niestety w rzeczywistości będzie ono wyższe, dlatego że nie wszystkie dane o upadłych przedsiębiorstwach są dostępne. 

Jak możemy poprawnie oszacować to prawdopodobieństwo? Na początek dajemy szansę 50:50, czyli albo firma przetrwa, albo nie przetrwa z równym prawdopodobieństwem. Z punktu widzenia badania oznacza to, że spośród 7147 nie-bankrutów losujemy 182, uzyskując sumaryczną próbę 364. Dzięki temu dostajemy równy podział bankrutów do niebankrutów, co odzwierciedla pomysł początkowego prawdopodobieństwa a priori 0,5. Następnie stosujemy najlepsze metody oceny zagrożenia bankructwa, jak sieci neuronowe, drzewa klasyfikacyjne, analiza dyskryminacyjna czy logit. Wszystkie one zawierają pewien próg zagrożenia i jeśli go przekroczą, to znaczy, że istnieje zagrożenie. Jeżeli nie przekroczy - nie ma zagrożenia. Ale ten brak zagrożenia jest tylko teoretyczny, bo zdarzają się błędy. I te błędy właśnie nas interesują - to będzie nasze prawdopodobieństwo straty.

Aby zwiększyć wiarygodność badania, powszechną praktyką jest podzielenie próby na zbiór uczący i testowy. Jeżeli zbiór testowy zawiera mniej więcej tyle samo danych co zbiór uczący, to powinniśmy użyć wyników ze zbioru testowego. Liczbę błędów dzielimy przez całkowitą liczbę przedsiębiorstw wybranych do próby, po to aby uzyskać prawdopodobieństwo straty (braku zysku).

Z punktu widzenia inwestora obligacyjnego, który raczej będzie trzymał obligacje co najmniej rok, interesująca jest jedynie ocena błędu predykcji na dwa lata przed upadłością. Najłatwiej użyć gotowy model dyskryminacyjny i logit. Wybrałem ten pierwszy (co do tego drugiego mam pewne wątpliwości czy jego empiryczna postać jest poprawna). Model jest banalny:

Z = 0,0896 + 1,9909*X1  - 1,214*X2

gdzie

X1 = Zdolność spłaty zadłużenia = (Zysk netto + Amortyzacja) / Zobowiązania

X2 = 1 / (Wskaźnik obciążenia zobowiązań krótkoterminowych kosztami operacyjnymi) = Koszty operacyjne / Zobowiązania krótkoterminowe

Dodatnia wartość oznacza brak zagrożenia, ujemna, że firma jest zagrożona. Dla przypomnienia model dotyczy firm przemysłowych, co odpowiada Orlenowi. Interesują nas dane roczne. Na podstawie danych na biznesradar.pl dostajemy w mln zł:

Zysk netto = 14 359

Amortyzacja = 14 731

Koszty operacyjne = 325 027

Zobowiązania krótkoterminowe = 66 496

Po podstawieniu Z = 0,37 > 0, czyli spółkę uznajemy za zdrową.

Warunek konieczny dla inwestora jest spełniony. Można powiedzieć, że prawdopodobieństwo bankructwa jest mniejsze niż 0,5, a teraz chcemy oszacować dokładniejszą wartość. Wobec tego przechodzimy do analizy błędów. Autorzy pokazują następującą tabelę/macierz pomyłek:

Źródło: [1]

W zbiorze testowym 74 przedsiębiorstw znajduje się 7 bankrutów błędnie sklasyfikowanych jako niebankruty. Oznacza to, że prawdopodobieństwo straty wynosi p = 7 / 74 = 0,095. 

Zauważmy jednak, że w zbiorze uczącym jest dużo więcej danych (172) i w tym zbiorze pomyłek prawdopodobieństwo straty wynosi: 20 / 172 = 0,116. Wg mnie podział powinien być mniej więcej równy, aby obiektywnie ocenić model. Oczywiście rozumiem zamysł, że zbiór uczący powinien być jak największy, aby model mógł się "nauczyć" prawidłowych zależności. I nawet bym się z tym zgodził gdyby nie jeden szkopuł. Mianowicie, na moją logikę, model na zbiorze uczącym powinien wypadać lepiej niż na testującym. No skoro stworzył zależności na podstawie danych, to jak na teście miałby wypadać jeszcze lepiej? Jedynie przez przypadek. Zbiór uczący powinien być więc maksymalizowany, ale pod warunkiem, że testowy nie daje lepszych wyników.

Biorąc powyższe pod uwagę uznam, że p = 0,11. W tym miejscu trzeba zaznaczyć, że sieci neuronowe dają lepsze wyniki niż analiza dyskryminacyjna i zarówno na zbiorze uczącym jak i testowym p wyniosłoby wtedy zaledwie 9 / 172 = 0,052. Oznacza, że można zmniejszyć ryzyko dwukrotnie. Na chwilę to zostawmy.

Wróćmy do naszej analizy wartości oczekiwanej obligacji, tj. wzoru (1). Wstawiamy za p = 0,11. Dla PCC Rokity, która była moim benchmarkiem, przyjąłem x = 9%. Stąd:

W = 0,11*0 + (1-0,11)*9% = 8%

Zatem oczekiwana rentowność paroletniej obligacji korporacyjnej wynosi 8%. Zauważmy, że jest dość mało biorąc pod uwagę, że stopa wolna od ryzyka = 7%. Ale niech będzie.

Mając dwa punkty (7 i 8) chcemy znaleźć zależność między W a p. Mamy dwa punkty 

W1 = 7% dla p = 0

W2 = 8% dla p = 0,11

Powstaje pokusa, aby utworzyć funkcję liniową między r a p:

Jest to błędne założenie, bo przecież dla p = 1 dostalibyśmy pewną wartość (mniej niż 20%), a przecież nikt przy zdrowych zmysłach nie będzie inwestował w coś, co na 100% nie przyniesie zysku czy przyniesie stratę. Oczekiwany zysk powinien dążyć do nieskończoności dla p = 1. Widzimy więc, że prawdziwa zależność jest nieliniowa, mimo iż wartość oczekiwana jako funkcja jest liniowa. Wynika to z tego, że wartość oczekiwana jest funkcją nie tylko p, ale też potencjalnego zysku (x), którego na tym wykresie nie widać, choć wiemy, że dla p = 0,11 wynosi x = 9%. Nie wiemy jednak, ile wyniesie p, jeśli np.  x = 15%. 

Oczywiście dzięki teorii CAPM wiemy, że r jest liniową funkcją ryzyka systematycznego, a ten pośrednio zależy od p. Ale nie chcemy stosować tutaj klasycznej wersji tego modelu, bo nie szukamy prawdziwego kosztu kapitału własnego, tylko abstrakcyjnego (minimalnego), który zakłada, że spółka będzie wypłacać co najwyżej minimalne dywidendy. Stąd nasze podejście jest bardziej teoretyczne. Teoria jednak będzie ważna, jeśli będzie racjonalna.

CAPM jest modelem dość otwartym, w tym sensie, że może być rozszerzony albo zmodyfikowany. Jedną z takich modyfikacji jest zastąpienie miary ryzyka entropią. Powstało wiele prac w tym temacie, np. [2, 3, 4, 5], pierwsza już na początku lat 70 ub. w. Entropia jest tylko funkcją jednej zmiennej - prawdopodobieństwa, więc możemy spróbować przekształcić nasze p w entropię. Wtedy rzeczywiście można będzie uzyskać liniową zależność między oczekiwaną stopą dochodu a ryzykiem. 

Żeby nie było wątpliwości - model, który tu zastosuję nie będzie idealnie poprawny w sensie teoretycznym. W teorii powinno się znaleźć, w uproszczeniu, prawdopodobieństwo zysku (straty) pod warunkiem, że portfel rynkowy osiąga zysk (stratę) - jeżeli korelacja między nimi jest dodatnia. Gdyby była ujemna, to szukane będzie prawdopodobieństwo zysku (straty) pod warunkiem, że portfel rynkowy osiąga stratę (zysk). Zwróćmy uwagę, że ze względu na posługiwanie się dodatnią wartością oczekiwaną, w naszym przypadku mamy zarówno jedno jak i drugie, tj. p odpowiada za straty, a 1-p za zyski, lecz średnia rynkowa pozostaje dodatnia. W modelu analizujemy jedynie ten mniej prawdopodobny scenariusz zagrożenia niewypłacalności, a jest praktycznie niemożliwe, aby cały rynek (ważony kapitalizacjami o najlepszym składzie) stał się niewypłacalny. Kwestię korelacji całkowicie pomijam w tym modelu, natomiast zważmy, że akurat Orlen jest mocno skorelowany z WIGiem.

Entropia jest średnią ważoną swoją własną informacją: jeśli mamy informację p_i, którą zapisujemy w postaci ujemnego logarytmu o podstawie 2:

to entropia będzie wtedy wartością oczekiwaną po wszystkich p_i:

W naszym binarnym modelu H przyjmie postać

W ogólnej wersji podstawa 2 nie jest konieczna (zob. szybkie wyprowadzenie wzoru na entropię), ale w naszym modelu jest istotna. Dla tej podstawy H zachowuje się następująco: 

- dla p = 0, H = 0

- dla p = 0,5, H = 1 = max

- dla p = 1, H = 0

Wykres funkcji H(p):

Porównując z poprzednimi tezami, zauważmy, że nie dostajemy tego, czego pierwotnie oczekiwaliśmy, bo im bliżej 1, tym p spada do zera. Wartość oczekiwana miała dążyć wtedy do nieskończoności, a tu zamiast tego wraca do zysku osiąganego bez ryzyka. O co tu chodzi? Wynika to z ukrytego założenia, że można grać na spadki. W końcu każde p różne od 0,5 oznacza mniejszą niepewność, co się wydarzy. Przy oczywistej stracie, czyli dużym p, należy zająć pozycję krótką, osiągając niewielki, ale dodatni zysk. W sumie p > 0,5 oznacza zwykłą redundancję, więc wystarczy, że ograniczymy p do zakresu od 0 do 0,5.

Tworzymy więc model a'la CAPM oparty na entropii o postaci:

(2) r = Rf + b*H

gdzie

r - oczekiwana stopa zwrotu z aktywa (tu Orlen)

Rf - stopa wolna od ryzyka

H - entropia (zamiast bety)

b - pewna stała (w CAPM średnia rynkowa stopa zwrotu minus stopa wolna od ryzyka)

Zapiszmy jeszcze raz nasze dane podstawione do (1), uwzględniając H:

W1 = 7% dla p = 0 => H = 0

W2 = 8% dla p = 0,11 => H = 0.5

Podstawmy je do (2), bo W musi być równe r:

8 = 7 + b*0.5

b = 2

Dostajemy funkcję:

r = 7 + 2*H

Teraz możemy sprawdzić, ile powinno wynieść H i p dla r = 9,2. Po podstawieniu do formuły dostalibyśmy H = 1,1. Ale przecież maksymalne H wynosi 1! Powstaje błąd. Okazuje się, że wybrana stopa r jest za duża. 

Ten błąd to konsekwencja błędnej postaci równania. Od początku błędem było przyjęcie p = 0,11. Przypominam, że wziąłem je na podstawie błędów analizy dyskryminacyjnej, która po pierwsze była podzielona na zbiór uczący i testowy, a ja posłużyłem się tym uczącym; a po drugie nie była najlepszą metodą szacowania zagrożenia. Lepsze były sieci neuronowe generujące p = 0,052. Nie mogłem od tak po prostu przyjąć tej niższej wartości, bo musiałbym najpierw mieć gotowy model tych sieci i sprawdzić na nim, czy spółka rzeczywiście nie niesie poważnego zagrożenia niewypłacalności. W sumie jednak rzeczywiście prawdopodobieństwo niewypłacalności będzie mniejsze niż 0,1. Zrobię więc poprawkę przyjmując p w dwóch wersjach: na podstawie błędów zbioru testowego analizy dyskryminacyjnej (p = 0,095), a potem na po podstawie sieci neuronowych (p = 0,052).

Wariant 1: dla p = 0,095

Zaczynamy od początku:

W = 0,095*0 + (1-0,095)*9% = 8.15%

W1 = 7% dla p = 0 => H = 0

W2 = 8,15% dla p = 0,095 => H = 0.45

Stąd

8,15 = 7 + b*0,45

b = 2.56

Dostajemy równanie:

r = 7 + 2.56*H

Podstawiamy za r 9,2 i znajdujemy H oraz p:

9,2 = 7 + 2,56*H

Stąd:

H = 0.86 => p = 0,28

Otrzymany wynik wskazywałby, że r = 9,2% uzyskujemy dla p = 0,28. Czyli prawdopodobieństwo niewypłacalności minimalnej dywidendy jest niemal 3 razy większe niż ryzyko niewypłacalności odsetek z obligacji. Możemy więc narysować tę funkcję - oczekiwana stopa zwrotu będzie liniowo zależna od niepewności poniesienia straty:

Wariant 2: dla p = 0,052

W = 0,052*0 + (1-0,052)*9% = 8.53%

W1 = 7% dla p = 0 => H = 0

W2 = 8,53% dla p = 0,052 => H = 0.295

Stąd

8,53 = 7 + b*0,295

b = 5,19

Dostajemy funkcję:

r = 7 + 5,19*H

Podstawiamy za r 9,2 i znajdujemy H oraz p:

9,2 = 7 + 5,19*H

H = 0.42 => p = 0,085

I wykres 

Różnica jest diametralna. Jeśli chcemy wybrać jeden z tych dwu wariantów, musimy sobie odpowiedzieć na pytanie, które prawdopodobieństwo (subiektywne) jest bardziej poprawne: 0,28 czy 0,085. Właściwie, to odpowiedź jest dość jednoznaczna - to pierwsze. W tym drugim przypadku odległość między ryzykiem obligacji komercyjnych a akcjami Orlenu jest bardzo niewielka - ledwo 0,03 (0,28 - 0,095 = 0,185 vs. 0,032 0,084 - 0,052 = 0,032), co jest dla mnie nie do zaakceptowania. Jeżeli więc przyjmujemy, że r = 9,2%, to prawdopodobieństwo, że Orlen nie wypłaci minimalnych dywidend wynosi niecałe 0,3.

Problem polega na tym, że naszym celem nie było oszacowanie p, tylko znalezienie odpowiedzi czy r = 9,2% jest prawidłowe. Gdyby pierwszy wariant zachować, to odpowiedź byłaby twierdząca - 28% uznalibyśmy raczej za rozsądny poziom zagrożenia, może nawet w jego górnych granicach. Jeżeli jednak chcemy posłużyć się drugim wariantem, to okaże się, że 9,2% stanowi za niską stopę dyskontową w naszym modelu dyskontowym.   

Co by się stało, gdybyśmy zrównali poziom p z drugiego wariantu do pierwszego? Podstawmy więc w drugim wariancie p = 0,28:

r = 7 + 5,19*H(p = 0,28)

r = 11,44

Zobaczmy, jak zachowa się wycena przy tej stopie dyskontowej:

Scenariusze A (brak zmiany stopy procentowej)

53-56 zł to lekka przesada. Jednak mamy też scenariusze ze spadającymi stopami i wtedy już pojawią się realne poziomy.

Scenariusze B (spadek stopy o 0,5 pkt proc.)

Scenariusze C (stopniowy spadek stopy o 1,5 pkt proc.)

Przyznanie startowej stopie dyskontowej 11,4% może mieć sens tylko jeśli uwzględnimy jej spadek w przyszłości, a więc tylko uznając Scenariusz B i C. Z drugiej strony ciągle pamiętać musimy, że prawdziwy koszt kapitału własnego może być wyższy, bo zawiera cały potencjalny wzrost dywidendy, którego nie znamy. Wzrost dywidendy wynika ze wzrostu zysku, który globalnie byłby tożsamy ze wzrostem nominalnego PKB. Minimalne dywidendy rosną tylko o 3% rocznie, tj. na poziomie inflacji. Faktyczne dywidendy mogą rosnąć o kolejne 2-3%, chociaż warto mieć gdzieś z tyłu głowy słowa polityków obecnie rządzących kwestionujących jakiekolwiek zyski Orlenu. Gdyby dodać jeszcze 2-3 pkty proc., podniosłoby to r do 13,4-14,4%. Jest to sporo dla Orlenu nawet przy założeniu spadającej stopy (procentowej, a więc i dyskontowej) o 1,5 pkt proc. (Scenariusz C), bo dostaniemy ok. 12-13% w modelu rezydualnym.

W tym miejscu tylko napomknę, że obniżenie stopy od 0,5 do 1,5 pkt proc. jest wiarygodne. Średnia referencyjna stopa NBP od roku 2000 do 2023 r. wynosi 5,2%. Z kolei od 2003 do 2023 wynosi ok. 4,3%. Stopa ta nie jest zmienną stacjonarną, więc nie można opierać się na jej średniej, ale może być to punkt wyjścia. 

Nasz problem nie dotyczy zatem stopy procentowej, ale przyjętego prawdopodobieństwa straty: musimy sobie odpowiedzieć na pytanie, jakie jest rzeczywiście wg nas prawdopodobieństwo, że Orlen może nie być w stanie wypłacać - co tu mówić - naprawdę niskich dywidend? Ostatnie wiadomości są dla spółki negatywne, ciąży nad nią ryzyko polityczne, tzn. kolejne obciążenia. Warto też dopowiedzieć, że sprawa jest rozwojowa, bo nagła zmiana zarządu spółki powoduje z jednej strony pewne oczyszczenie, z drugiej  większą niepewność co do kierunku. Rynek powinien otrzymać jasny komunikat od spółki, że jej polityka dywidendowa nie ulegnie zmianie. Wtedy zagrożenie by spadło. Brak takich komunikatów powoduje, że większy kapitał, z funduszami włącznie, będzie się obawiał inwestowania. 

Łącząc powyższe w całość, jestem skłonny przyjąć wysoki poziom p = 0,28, pod warunkiem, że przyjmiemy, że faktyczne dywidendy będą równe minimalnym dywidendom albo że będą rosły niewiele powyżej, np. 0,5 pkt proc. Wtedy nasza stopa dyskontowa na poziomie 11,4% stanie się całkiem rozsądna.

Dodatkowym argumentem niech będą analizy Damodarana z premiami za ryzyko dla każdego kraju (zob. link). Na chwilę obecną premię tę dla Polski wyznaczono na poziomie 5,84%. Aby ją obliczyć dodaje się premię za ryzyko krajowe do premii dla USA. Dla USA premia wynosi 4,6% (ryzyko krajowe USA = 0, bo traktuje się jak benchmark). Premia za ryzyko krajowe Polski wynosi 1,24%, stąd 4,6 + 1,24 = 5,84%. Dodajmy więc obecny WIBOR3M = 5,86% i otrzymamy 11,7%. Czyli blisko tego co nam tu wychodzi.

Ostatecznie, wykres entropicznego SML wyglądałby następująco:

A zależność między oczekiwaną stopą zwrotu a samym prawdopodobieństwem strat / utraty zysku prezentowałaby się tak:

    

Muszę powtórzyć, że ten r = 11,4% i odpowiadające jej p = 0,28 to poziomy na chwilę obecną. To znaczy, wycena która wychodzi w granicach od 56,6 do 67,3 jest na tę chwilę bardziej prawdopodobna niż te wcześniejsze (powyżej 70).

Arkusz z wyceną

Literatura:

[1] Pociecha J., Pawełek B. , Baryła M., Augustyn S. Statystyczne metody prognozowania bankructwa w zmieniającej się koniunkturze gospodarczej. Wydawnictwo UE w Krakowie, Kraków 2014;

[2] Philippatos, G. Entropy, Market Risk, and the Selection of Efficient Portfolios. Appl. Econ. 1972, 4, 209–220;

[3] Gulko, L. Dart boards and asset prices introducing the entropy pricing theory. Adv. Econom. 1997, 12, 237–276;

[4] Ou, J.S. Theory of portfolio and risk based on incremental entropy. J. Risk Finance 2005, 6, 31–39;

[5] Novais, R.G., Wanke, P., Antunes, J., Tan, Y. Portfolio optimization with a mean-entropy-mutual information model. Entropy 2022, 24, 369.

Modelowanie ryzyka z rugarch (język R)

Ryzyko można szacować i modelować na różne sposoby. Standardowo obliczamy wariancję stopy zwrotu i będzie to nawet poprawne, jeśli się ona nie zmienia. Pytanie tylko dlaczego uważamy, że powinna być stała? Co więcej, nawet gdy średnia wariancja się nie zmienia, to nie znaczy, że nie można znaleźć dokładniejszej miary ryzyka - taką jest wariancja warunkowa, która stanowi istotę procesu GARCH. 

Pakietu rugarch w R już używałem w tym wpisie , ale tym razem skupię się tylko na nim i zrobię przykład na WIG20. Ładujemy pakiet:

if (require("rugarch")==FALSE) {

  install.packages("rugarch")

}

  library("rugarch")

Dodatkowo załaduję "xts", który przyda się dla prawdziwych danych oraz "forecast" do symulacji ARMA.

if (require("xts")==FALSE) {

  install.packages("xts")

}

  library("xts")

if (require("forecast")==FALSE) {

  install.packages("forecast")

}

library("forecast")

Specyfikacja modelu

Stwórzmy sztuczny proces GARCH. Pierwsza sprawa to budowa teoretycznego modelu - specyfikacja. To się robi przy pomocy funkcji ugarchspec(). Na specyfikację składają się głównie 4 elementy:

1) model (funkcja) wariancji warunkowej: variance.model

2) model (funkcja) średniej warunkowej: mean.model

3) rozkład warunkowy zmian (np. stóp zwrotu, nie warunkowej wariancji): distribution.model

4) wartości parametrów (przy symulacji procesu należy podać wszystkie parametry modelu): fixed.pars

Ad 1) variance.model jako lista składa się głównie z dwóch części: rodzaju modelu (model) oraz rzędów (garchOrder). Z rodzajów modelu do wyboru mamy:

“sGARCH” - standardowy GARCH,

“eGARCH” - wykładniczy GARCH (The exponential GARCH)

“gjrGARCH” -  Glosten-Jagannathan-Runkle GARCH

“apARCH” - The Asymmetric Power ARCH

“iGARCH” - zintegrowany GARCH (The integrated GARCH)

 “csGARCH” - The Component sGARCH

“fGARCH” - full GARCH - rodzina modeli podzielona na podmodele: 

a) “GARCH” - znów sGARCH

b) “TGARCH” - progowy GARCH (The Threshold GARCH)

c) “AVGARCH” - The Absolute Value GARCH

 d) “NGARCH” - nieliniowy GARCH

e) “NAGARCH” - nieliniowy asymetryczny GARCH

f) “APARCH” -  znowu APARCH (chyba nie to samo)

g) “GJRGARCH”- znowu gjrGARCH (jak wyżej)

Drugim elementem tej części są rzędy, czyli garchOrder. Należy zwrócić uwagę, że jest to dokładna analogia do ARMA(p, q), z tym że kolejność jest odwrotna: najpierw było ARCH(q), czyli średnia krocząca wariancji warunkowej, a potem dołożono część autoregresyjną tej wariancji, w sumie GARCH(q, p). Standardowo i na początek zawsze używamy q = 1, p = 1. Rzędy będą wektorem, którego elementami będzie liczba rzędów przyporządkowana danemu parametrowi. Każdy model ma swoje parametry, tak że wybierając odpowiedni typ modelu należy mieć to na względzie przy zapisywaniu tego wektora. Czyli ARCH(1) zapiszemy jako garchOrder = c(1, 0), a GARCH(1, 1) jako  garchOrder = c(1, 1). 

Przykład 1: ugarchspec(variance.model = list(model = "sGARCH", garchOrder = c(1, 2)))

Przykład 2, dla podmodeli: ugarchspec(variance.model = list(model = "fGARCH", submodel = "NGARCH", garchOrder = c(1, 1)))

Ad 2) mean.model  jako lista zawiera dwie podstawowe części: armaOrder oraz external.regressors. Jest to po prostu ARMAX dla zmiennej, jak stopa zwrotu. Pierwszą z wymienionych części stosujemy analogicznie jak dla garchOrder. Druga część to zmienne egzogeniczne, czyli zewnętrzne regresory ARMAX. Specjalnym przypadkiem ARMAX jest GARCH-in-Mean, w którym za zmienną egzogeniczną wstawiamy samą wariancję warunkową (lub jej pierwiastek). Jest to ciekawy przykład sprzężenia zwrotnego między średnią warunkową a jej wariancją, np. między oczekiwaną (warunkową) stopą zwrotu a jej ryzykiem. Nie musimy jednak sami wyciągać tej wariancji i przyłączać do modelu, bo taki model jest do dyspozycji tutaj. Po prostu zamiast external.regressors stosujemy dodatkowy argument archm = TRUE. 

Przykład1: ugarchspec(variance.model = list(model = "sGARCH", garchOrder = c(1, 1)), mean.model = list(armaOrder = c(1, 1)))

Przykład2: ugarchspec(variance.model = list(model = "sGARCH", garchOrder = c(1, 1)), mean.model = list(armaOrder = c(1, 0), archm = TRUE))

Warto dodać, że w tej części także można ustalić czy średnia ma się zachowywać zgodnie z procesem ARFIMA.

Ad 3) distribution.model, tj. rozkład prawdopodobieństwa naszej zmiennej może to być:

“norm” - rozkład normalny

“snorm” - skośno-normalny (skew-normal distribution)

“std” - t-Studenta

“sstd” skośny t-studenta (skew-student), 

“ged” - uogólniony rozkład błędów (the generalized error distribution), 

“sged” - skośny uogólniony rozkład błędów (the skew-generalized error distribution), 

“nig” - normalny odwrotny rozkład gaussowski (the normal inverse gaussian distribution), 

“ghyp” - uogólniony hiperboliczny (the Generalized Hyperbolic),

“jsu” - Johnson’s SU distribution (SU to nie skrót, ale po prostu nazwa zmiennej w tym rozkładzie, podobnie jak litera "t" w t-Studenta).

Przykład: ugarchspec(variance.model = list(model = "sGARCH", garchOrder = c(1, 2)), distribution.model = "norm")

Ad 4) fixed.pars używamy w zasadzie tylko do symulacji. Ustalamy wartości parametrów dla wybranego modelu. Nazewnictwo parametrów:

alpha1, alpha2, ... dla ARCH(q)

beta1, beta2, ..., dla GARCH(p)

omega - wyraz wolny funkcji wariancji

gamma1, gamma2, ...  dla asymetrii, tj. APARCH, EGARCH i gjrGARCH

delta - siła asymetrii (APARCH)

vxreg1, vxreg2, ... dla zmiennych egzogenicznych (zewnętrznych regresorów) modelu wariancji

ar1, ar2, ... dla części AR

ma1, ma2, ... dla części MA

mu dla wyrazu wolnego ARMAX

archm - wspomniany ARCH-in-Mean

arfima jako ułamkowy rząd d

mxreg1, mxreg2, ... dla zmiennych egzogenicznych (zewnętrznych regresorów) w ARMAX

eta11, eta12, ... dla parametrów asymetrii obrotu (FGARCH)

eta22, eta21, ... dla parametrów asymetrii przesunięcia (FGARCH)

lambda - siła warunkowej sigmy (wariancji)

skew - dla skośności rozkładu badanej zmiennej

shape - kształt rozkładu 

ghlambda - lambda dla rozkładu "ghyp"

Przykład 1, dla rozkładu normalnego: 

ugarchspec(variance.model = list(model = "sGARCH", garchOrder = c(1, 1)), 

                       distribution.model = "norm", fixed.pars = list(omega = 0.5, 

                                                                      alpha1 = 0.3, 

                                                                      beta1 = 0.2, 

                                                                      mu = 0.000001,

                                                                      ar1 = 0.000001,

                                                                      ma1 = 0.000001))

Przykład 2, dla skośnego rozkładu t-Studenta: 

ugarchspec(variance.model = list(model = "sGARCH", garchOrder = c(1, 2)), 

                       distribution.model = "sstd", fixed.pars = list(omega = 0.5, 

                                                                      alpha1 = 0.3,

                                                                      beta1 = 0.2,

                                                                      beta2 = 0.1, 

                                                                      mu = 0.000001,

                                                                      ar1 = 0.000001,

                                                                      ma1 = 0.000001,

                                                                      skew = 1.5,

                                                                      shape = 5))

Symulacja procesu GARCH

Symulację wykonamy za pomocą funkcji ugarchpath(). Głównymi argumentami są wybrany model (ze specyfikacji) oraz liczba danych. Funkcja zwraca nie tyle samą symulację, ale cały zestaw jej obiektów. Aby uzyskać same wartości, najłatwiej użyć funkcji fitted(). 

Przykład:

set.seed(3)

mojGarch <- ugarchspec(variance.model = list(model = "sGARCH", garchOrder = c(1, 0)), 

                       distribution.model = "norm", fixed.pars = list(omega = 0.5, 

                                                                      alpha1 = 0.9, 

                                                                      mu = 0.000001,

                                                                      ar1 = 0.000001,

                                                                      ma1 = 0.000001))

symGarch <- ugarchpath(mojGarch, n.sim = 500)

symStopaZwrotu <- fitted(symGarch) 

# ewentualnie

#symStopaZwrotu <- symGarch@path$seriesSim

plot(symStopaZwrotu, type="l")

To co może zaskakiwać to to, że ustawiliśmy rozkład normalny, a wykres przypomina raczej rozkład z grubymi ogonami. Jednak jest to warunkowy rozkład normalny w tym sensie, że zależy od przeszłości. Sama zmienna (stopa zwrotu) jest tu niezależna od poprzednich wartości (ar1 i ma1  ustawione na zero), ale jej składnik losowy już tak. Składnik losowy jest po prostu procesem średniej kroczącej (normalnie nazywany MA, ale aby nie mylić z procesem dla samej zmiennej nazywany ARCH). 

Z symulacji możemy wydobyć też wariancję warunkową albo warunkowe odchylenie standardowe, tj. nasze ryzyko:

symGarch <- ugarchpath(mojGarch, n.sim = 500)

symStopaZwrotu <- fitted(symGarch) 

# ewentualnie

#symStopaZwrotu <- symGarch@path$seriesSim

plot(symStopaZwrotu, type="l")

symRyzyko <- sigma(symGarch)

# ewentualnie

#symRyzyko <- symGarch@path$sigmaSim

plot(symRyzyko, type="l")

Najlepiej połączyć obydwa wykresy w jeden: stopa zwrotu + jego zmienne odchylenie:

zakresY <- c(min(symStopaZwrotu, -symRyzyko), max(symStopaZwrotu, symRyzyko))

plot.ts(symStopaZwrotu, ylim = zakresY)

lines(symRyzyko, col = "blue")

lines(-symRyzyko, col = "blue")

Model empiryczny

Powiedzmy, że dostajemy samą taką symulację bez znajomości modelu. Chcemy dopasować otrzymane dwa szeregi do odpowiedniego modelu GARCH. Stosujemy funkcję ugarchfit(). Najważniejsze jej argumenty to dane (data), wybrany model (spec) oraz liczba prognoz poza próbą (out.sample). Zakładamy, że nic nie wiemy o próbie, więc na początek tworzymy standardowy sGARCH  - oczywiście tym razem bez ustalania parametrów, bo mamy zadanie je dopiero oszacować. Za dane podstawiamy wcześniej zdefiniowaną zmienną symStopaZwrotu:

mojGarch <- ugarchspec(variance.model = list(model = "sGARCH", garchOrder = c(1, 1)), mean.model = list(armaOrder = c(1, 1)))

dopasGarch <- ugarchfit(spec = mojGarch, data = simArch, out.sample = 0)

print(dopasGarch)

*---------------------------------*
*          GARCH Model Fit        *
*---------------------------------*

Conditional Variance Dynamics 	
-----------------------------------
GARCH Model	: sGARCH(1,1)
Mean Model	: ARFIMA(1,0,1)
Distribution	: norm 

Optimal Parameters
------------------------------------
        Estimate  Std. Error  t value Pr(>|t|)
mu      0.039416    0.040145  0.98183  0.32618
ar1    -0.427181    0.391769 -1.09039  0.27554
ma1     0.480952    0.368062  1.30671  0.19131
omega   0.598849    0.071227  8.40760  0.00000
alpha1  0.804083    0.103489  7.76977  0.00000
beta1   0.005350    0.016619  0.32191  0.74752

Robust Standard Errors:
        Estimate  Std. Error  t value Pr(>|t|)
mu      0.039416    0.042395  0.92975  0.35250
ar1    -0.427181    0.358426 -1.19183  0.23333
ma1     0.480952    0.327567  1.46826  0.14203
omega   0.598849    0.065481  9.14534  0.00000
alpha1  0.804083    0.103111  7.79820  0.00000
beta1   0.005350    0.006337  0.84419  0.39856

LogLikelihood : -797.842 

Information Criteria
------------------------------------
                   
Akaike       3.2154
Bayes        3.2659
Shibata      3.2151
Hannan-Quinn 3.2352

Weighted Ljung-Box Test on Standardized Residuals
------------------------------------
                        statistic p-value
Lag[1]                      1.067  0.3016
Lag[2*(p+q)+(p+q)-1][5]     1.357  0.9994
Lag[4*(p+q)+(p+q)-1][9]     3.017  0.8880
d.o.f=2
H0 : No serial correlation

Weighted Ljung-Box Test on Standardized Squared Residuals
------------------------------------
                        statistic p-value
Lag[1]                    0.02626  0.8713
Lag[2*(p+q)+(p+q)-1][5]   0.21540  0.9914
Lag[4*(p+q)+(p+q)-1][9]   1.84882  0.9223
d.o.f=2

Weighted ARCH LM Tests
------------------------------------
            Statistic Shape Scale P-Value
ARCH Lag[3]  0.001223 0.500 2.000  0.9721
ARCH Lag[5]  0.274535 1.440 1.667  0.9470
ARCH Lag[7]  1.653454 2.315 1.543  0.7901

Nyblom stability test
------------------------------------
Joint Statistic:  1.0574
Individual Statistics:              
mu     0.03849
ar1    0.33674
ma1    0.31603
omega  0.38146
alpha1 0.21883
beta1  0.27590

Asymptotic Critical Values (10% 5% 1%)
Joint Statistic:     	 1.49 1.68 2.12
Individual Statistic:	 0.35 0.47 0.75

Sign Bias Test
------------------------------------
                   t-value   prob sig
Sign Bias           0.9554 0.3399    
Negative Sign Bias  0.1454 0.8845    
Positive Sign Bias  0.2359 0.8136    
Joint Effect        1.2101 0.7506    


Adjusted Pearson Goodness-of-Fit Test:
------------------------------------
  group statistic p-value(g-1)
1    20     16.00       0.6573
2    30     28.96       0.4672
3    40     34.40       0.6796
4    50     53.60       0.3023

Wydruk dostarcza nie tylko estymacji współczynników, ale też wszystkich potrzebnych informacji o poprawności modelu. Wykonujemy jego diagnostykę.

 Są dwie wersje testowania istotności parametrów. Pierwsza to konwencjonalna metoda największej wiarygodności (Optimal parameters), a druga odporna na nieprawidłowe założenie rozkładu (Robust Standard Errors). Ta druga jest więc mocniejsza i powinniśmy na nią patrzeć jako pierwszą. Parametry się w niej nie zmieniają, a jedynie ich przedziały istotności. Widzimy, że jedynie istotne są omega i alpha1, czyli poprawnie, natomiast same ich wartości też dość dobrze oszacowane (alpha1 jest równy 0.9, a oszacowano go na 0.8; omega równa się 0.5, a w estymacji = 0.6). Oczywiście widząc, że beta1 oraz ma1 są nieistotne, moglibyśmy poprawić teraz model. Dokończmy jednak najpierw diagnostykę.

Dalej mamy kryteria informacyjne (Information Criteria), które w tym wypadku nic nam nie powiedzą, bo nie porównujemy modelu z innym.

Ważony test Ljunga-Boxa sprawdzamy na dwóch poziomach: resztach (Weighted Ljung-Box Test on Standardized Residuals) oraz kwadratach reszt (Weighted Ljung-Box Test on Standardized Squared Residuals). Jeśli p-value > 0.05, to możemy przyjąć, że nie występują autokorelacje w pierwszym przypadku  w resztach, w drugim - w kwadratach reszt. Ponieważ p-value dla wielu rzędów q i p jest mocno powyżej 0.05, przyjęty model jest poprawny.

Podobnym testem jest Weighted ARCH LM, ale skupia się na samym efekcie ARCH, a dokładniej czy przyjęty model nie pominął tego efektu, np. dla pewnego rzędu. Jeżeli p-value > 0.05, to znaczy, że nie pominął, w przeciwnym wypadku prawdopodobnie pominął. Widzimy, że dla wielu rzędów q i p jest mocno powyżej 0.05, przyjęty model jest poprawny.

Test Nybloma (Nyblom stability test) bada stabilność modelu, tzn. czy parametry zmieniają się w czasie. Jest to bardzo ważny test z punktu widzenia właśnie analizy finansowej. Joint Statistic: 1.0574 dotyczy stabilności całego modelu. Porównujemy to z teoretycznymi wartościami dla kolejnych p-value, szczególnie patrzymy na wartość korespondującą z 5% - tutaj jest to 1.68. Ponieważ 1.68 > 1.0574 , nie ma podstaw do odrzucenia hipotezy zerowej o stabilności modelu. Dodatkowa analiza dotyczy każdego współczynnika osobno. Patrzymy na Individual Statistic. Mamy tu współczynniki: 

mu  =  0.03849, ar1 = 0.33674, ma1 = 0.31603, omega  0.38146, alpha1 0.21883, beta1  0.27590

Wartości te porównujemy z wartością teoretyczną odpowiadającą 5% - wynosi 0.47. Ponieważ 0.47 jest większa od każdego wspołczynnika, to znaczy, że wszystkie parametry są stabilne, zarówno średniej, wariancji, jak i rozkładu.

Test błędu znaku (Sign Bias Test) pozwala z kolei ocenić czy w szeregu nie występują szoki dodatnie lub ujemne. Niekonsekwentne oznaczenie  prob sig to nic innego jak p-value. Zarówno dla dodatniego, ujemnego, jak i łącznego efektu, jest ono większe od 0.05, czyli szoki nie występują. Gdyby występowały, trzeba by zmienić model na EGARCH, APARCH, TGARCH lub gjrGARCH.

W końcu test dobroci dopasowania modelu (Adjusted Pearson Goodness-of-Fit Test) sprawdza czy rozkład reszt jest odpowiedni. Mamy tu podział na kolejne kwantyle, tak że możemy zobaczyć jak reszty się zachowują w całym rozkładzie. Jeśli p-value > 0.05 dla któregoś kwantyla, znaczyłoby, że przyjęty rozkład jest niewłaściwy. W tym wypadku wszystkie wskazują poprawność rozkładu - przyjęliśmy normalny i oceniony jako też normalny.

Diagnostyka zakończona. Tutaj warto wspomnieć ciekawą opcję, którą można by nazwać graficzną diagnostyką. Wystarczy wpisać:

plot(dopasGarch)

i dostaniemy listę:

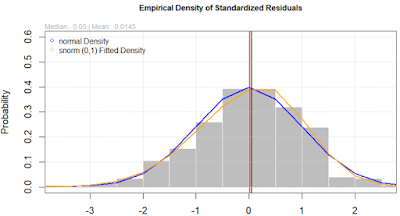
Make a plot selection (or 0 to exit): 1: Series with 2 Conditional SD Superimposed 2: Series with 1% VaR Limits 3: Conditional SD (vs |returns|) 4: ACF of Observations 5: ACF of Squared Observations 6: ACF of Absolute Observations 7: Cross Correlation 8: Empirical Density of Standardized Residuals 9: QQ-Plot of Standardized Residuals 10: ACF of Standardized Residuals 11: ACF of Squared Standardized Residuals 12: News-Impact Curve

Wybór:

Wybierzmy 8:

Dzięki tej opcji możemy naocznie ocenić poprawność przyjętego rozkładu.

Również zamiast testu dobroci możemy użyć wykresu kwantylowego (QQ), tzn. wybieramy z listy 9:

Tak jak wspomniałem, skoro niektóre parametry okazały się nieistotne, to moglibyśmy teraz model poprawić, tak że kod wyglądałby następująco:

mojGarch <- ugarchspec(variance.model = list(model = "sGARCH", garchOrder = c(1, 0)), mean.model = list(armaOrder = c(0, 0)))

dopasGarch <- ugarchfit(spec = mojGarch, data = symStopaZwrotu, out.sample = 0)

print(dopasGarch)

Poniżej wydruk tylko kilku pierwszych statystyk:

*---------------------------------*
*          GARCH Model Fit        *
*---------------------------------*

Conditional Variance Dynamics 	
-----------------------------------
GARCH Model	: sGARCH(1,0)
Mean Model	: ARFIMA(0,0,0)
Distribution	: norm 

Optimal Parameters
------------------------------------
        Estimate  Std. Error  t value Pr(>|t|)
mu      0.039045    0.039600  0.98599  0.32414
omega   0.617144    0.067416  9.15423  0.00000
alpha1  0.800232    0.102546  7.80364  0.00000

Robust Standard Errors:
        Estimate  Std. Error  t value Pr(>|t|)
mu      0.039045    0.042187  0.92552  0.35469
omega   0.617144    0.063213  9.76291  0.00000
alpha1  0.800232    0.102620  7.79800  0.00000

LogLikelihood : -799.3085 

Information Criteria
------------------------------------
                   
Akaike       3.2092
Bayes        3.2345
Shibata      3.2092
Hannan-Quinn 3.2192

Chociaż wiemy już, że drugi model jest lepszy, to aby ocenić to obiektywnie, porównamy ich kryteria informacyjne, które właśnie tutaj się przydadzą. Jeżeli wszystkie kryteria: AIC, BIC, SIC i HQIC wskazują mniejsze wartości, to znaczy, że ten model jest lepszy. Tak rzeczywiście się dzieje

Akaike       3.2092 < 3.2154

Bayes        3.2345 < 3.2659

Shibata      3.2092 < 3.2151

Hannan-Quinn 3.2192 < 3.2352

Otrzymujemy jednoznaczny wniosek, że ten drugi model jest lepszy od pierwszego.

Prognoza

Mając dobry model możemy przejść do prognozy. Prognozę można wykonać zarówno dla stopy zwrotu, jak i jej ryzyka. Ale ponieważ prognoza stopy zwrotu = oczekiwana stopa zwrotu, to znaczy, że w naszym przypadku jest to po prostu wyraz wolny bliski zera (nie mamy tu procesu ARMA), więc tak naprawdę interesuje nas tylko prognoza ryzyka. Prognozę wykonujemy przy pomocy ugarchforecast(). Jej główne argumenty to

1. fitORspec: model empiryczny z ugarchfit, ewentualnie model teoretyczny z podaniem danych

2. n.ahead: długość okresu prognozy

3. n.roll: ile razy wykorzystać do prognozy te obserwacje spoza próby (out of sample), które wcześniej były prognozowane zgodnie z n.ahead

4. ile ostatnich danych ma być zachowanych poza testowaną próbą (out.sample)

Punkty 3 i 4 są powiązane i na razie je zostawiam.

Stworzymy prognozę dla pięciu nowych punktów:

noweOkresy <- 5

prognozaGarch <- ugarchforecast(dopasGarch, n.ahead = noweOkresy)

prognozaStopaZwrotu <- fitted(prognozaGarch)

prognozaRyzyko <- sigma(prognozaGarch)

Aby zobaczyć to wszystko graficznie, powinniśmy połączyć próbę z prognozą. Jednak łączenie różnych typów danych i pokazywanie na wykresie może być w R wyzwaniem. Ponieważ działamy na szeregach czasowych, to najpierw zamieńmy wszystkie dane na ts i połączymy z prognozą:

# zamiana na ts i łączenie z prognozą

stopaZwrotu <- as.ts(symStopaZwrotu)

ryzyko <- as.ts(symRyzyko)

ostatniOkres <- end(stopaZwrotu)

dlugoscProby <- length(stopaZwrotu)

stopaZwrotu <- ts(c(as.numeric(stopaZwrotu), rep(NA, noweOkresy)), start = start(stopaZwrotu))

prognozaStopaZwrotu <- ts(c(stopaZwrotu[dlugoscProby], as.numeric(prognozaStopaZwrotu)), start = ostatniOkres)

ryzyko <- ts(c(symRyzyko, rep(NA, noweOkresy)), start = start(stopaZwrotu))

prognozaRyzyko <- ts(c(ryzyko[dlugoscProby], as.numeric(prognozaRyzyko)), start = ostatniOkres)

Pokażmy 30 ostatnich obserwacji i 5 nowych

# wykres

zakresX <- c(dlugoscProby - 30, length(stopaZwrotu))

zakresY <- c(min(na.omit(stopaZwrotu), -na.omit(ryzyko)), max(na.omit(stopaZwrotu), -na.omit(ryzyko)) + 2)

plot(stopaZwrotu, xlim=zakresX, ylim=zakresY, lwd=2)

lines(prognozaStopaZwrotu, lwd=2, col="green")

lines(ryzyko, lwd=2, col="red")

lines(-ryzyko, lwd=2, col="red")

lines(prognozaRyzyko, lwd=2, col="brown")

lines(-prognozaRyzyko, lwd=2, col="brown")

legend(x="topleft", legend=c("stopa zwrotu", "prognoza stopy zwrotu", "modelowane ryzyko", 

                             "prognoza ryzyka"), lwd=c(2,2,2,2), col=c("black",

                                                                       "green",

                                                                       "red",

                                                                       "brown"))

Ostatnia symulacja testowa

Na koniec przeprowadzę ostatnią symulację i jej test. Tym razem na odwrót - stworzę zwykły proces AR(1) o 500 obserwacjach i sprawdzę jak rugarch radzi sobie z tym, gdy ma zły model.

set.seed(3)

symStopaZwrotu = arima.sim(list(order=c(1,0,0), ar=0.6), n=500, mean=1)

mojGarch <- ugarchspec(variance.model = list(model = "sGARCH", 

                                             garchOrder = c(1, 1)), 

                       mean.model = list(armaOrder = c(1, 0)))

dopasGarch <- ugarchfit(spec = mojGarch, data = symStopaZwrotu, out.sample = 0)

print(dopasGarch) 

Częściowy wydruk:

Robust Standard Errors:
        Estimate  Std. Error   t value Pr(>|t|)
mu      2.607355    0.115327    22.608  0.00000
ar1     0.605802    0.033249    18.220  0.00000
omega   0.001275    0.003960     0.322  0.74745
alpha1  0.000000    0.003644     0.000  1.00000
beta1   0.999000    0.000065 15463.568  0.00000

LogLikelihood : -724.7 

Information Criteria
------------------------------------
                   
Akaike       2.9188
Bayes        2.9610
Shibata      2.9186
Hannan-Quinn 2.9354

O ile algorytm prawidłowo oszacował ar1 na 0.6 i alpha1 na zero, o tyle błędnie przypisał becie 1. Ta pełna jedynka pokazuje, że nie możemy kierować się bezmyślnie samą istotnością: skoro beta równa się 1, to może znaczyć, że  model został źle wyspecyfikowany. Aby to ocenić, usuńmy betę ze specyfikacji:

mojGarch <- ugarchspec(variance.model = list(model = "sGARCH", 

                                             garchOrder = c(1, 0)), 

                       mean.model = list(armaOrder = c(1, 0)))

dopasGarch <- ugarchfit(spec = mojGarch, data = symStopaZwrotu, out.sample = 0)

print(dopasGarch)

Robust Standard Errors:
        Estimate  Std. Error  t value Pr(>|t|)
mu       2.60768    0.120767   21.593        0
ar1      0.60566    0.035427   17.096        0
omega    1.06510    0.081482   13.072        0
alpha1   0.00000    0.048245    0.000        1

LogLikelihood : -725 

Information Criteria
------------------------------------
                   
Akaike       2.9160
Bayes        2.9497
Shibata      2.9158
Hannan-Quinn 2.9292

Teraz widzimy, że model rzeczywiście był źle wyspecyfikowany, ponieważ wszystkie kryteria się poprawiły (mają mniejszą wartość). Jedynie omega zmieniła wartość, a więc to ją beta1 wcześniej psuła. Oczywiście w symulacji nie ustawialiśmy odchylenia standardowego, a więc zostało ono automatycznie ustalone na 1, a wobec tego jego kwadrat - omega - też musi się równać 1 i tyle też wyniosła estymacja (i również w końcu stała się istotna). Jedynym błędem jaki się nam ostał jest zbyt duży wyraz wolny (miał się równać 1). Ten błąd jednak nie wynika z błędnego algorytmu, bo gdy będziemy estymować zwykłą arimą:

arima(x=symStopaZwrotu, order=c(1,0,0))

dostaniemy to samo. Dopiero użycie MNK:

summary(lm(symStopaZwrotu[-1] ~ symStopaZwrotu[-length(symStopaZwrotu)]))

przyniesie prawidłowy wyraz wolny równy ok. 1. Na marginesie, w tej próbce akurat średnia arytmetyczna rzeczywiście równa się 2.6, co wynika po prostu z tego, że składa się ze średniej niewarunkowej i warunkowej. MNK lepiej oddziela te dwie części. Algorytmy dla ARIMA i GARCH są przeznaczone dla bardziej złożonych modeli, a nie zwykłego AR, stąd kosztem są takie błędy. 

Model na prawdziwych danych

Dzienne stopy zwrotu WIG20

Zakres czasu: 2023-04-21 - 2024-07-02, czyli ostatnie 300 sesji. Dane ściągnięte ze stooq.pl. Przygotowujemy analizę:

# ustawiamy folder roboczy

sciezka = r"(C:\testy)"

#zamieniam "\" na "/"

sciezka = gsub("\\", "/", sciezka, fixed=T)

setwd(sciezka_testy)

nazwaPliku = "wig20_d.csv"

plik <- read.csv(nazwaPliku)

cena <- plik$Zamkniecie

Obs <- 300

stopaZwrotu <- tail(diff(log(cena)), Obs)

okres <- as.Date(tail(plik$Data[-1], Obs))  

Zwracam uwagę, że używam logarytmicznej stopy zwrotu, co generalnie ułatwia nie tylko kodowanie, ale testowanie (zmienna staje się "bardziej" normalna). Ostatnie 300 stóp zwrotu WIG20 okazały się trudniejsze do modelowania niż sądziłem. Przykładowo, ten sam model co dla symulacji, okazał się niedobry, ponieważ parametr  ARCH(1) był nieistotny:

mojGarch <- ugarchspec(variance.model = list(model = "sGARCH", garchOrder = c(1, 1)), mean.model = list(armaOrder = c(1, 1)))

dopasGarch <- ugarchfit(spec = mojGarch, data = simArch, out.sample = 0)

print(dopasGarch)

*---------------------------------*
*          GARCH Model Fit        *
*---------------------------------*

Conditional Variance Dynamics 	
-----------------------------------
GARCH Model	: sGARCH(1,0)
Mean Model	: ARFIMA(0,0,0)
Distribution	: norm 

Optimal Parameters
------------------------------------
        Estimate  Std. Error  t value Pr(>|t|)
mu      0.000933    0.000713   1.3079  0.19092
omega   0.000153    0.000014  11.0540  0.00000
alpha1  0.000000    0.039697   0.0000  1.00000

Robust Standard Errors:
        Estimate  Std. Error  t value Pr(>|t|)
mu      0.000933    0.000661   1.4103  0.15844
omega   0.000153    0.000016   9.3305  0.00000
alpha1  0.000000    0.033403   0.0000  1.00000

LogLikelihood : 892.5 

Information Criteria
------------------------------------
                    
Akaike       -5.9298
Bayes        -5.8928
Shibata      -5.9300
Hannan-Quinn -5.9150

Zobaczmy z jak ogromną kombinacją parametrów do określenia mamy tu do czynienia: rodzaj modelu zarówno GARCH, jak i ARFIMA (w tym określenie czy GARCH umieścić w ARMA czy nie) , rzędy GARCH(q, p), rząd AR, rząd MA, typ rozkładu.  Wykonałem wiele testów i doszedłem (przynajmniej na dziś) do wniosku, że najlepszym modelem jest TGARCH(1, 1)-in-Mean z rozkładem skośno-normalnym. TGARCH uwzględnia inne zachowanie się warunkowej wariancji, gdy są spadki i inne, gdy są wzrosty. Dostajemy więc dużo dokładniejsze zmiany ryzyka w kolejnych okresach niż w standardowym GARCH. Nazwa TGARCH pochodzi od Threshold GARCH, czyli progowy GARCH. Progiem jest tu... zero, poniżej którego następuje przeskoczenie na parametr dla ujemnych zmian (nie jest to nic skomplikowanego, po prostu rozdziela się składnik losowy na część dodatnią i ujemną).  

 mojGarch <- ugarchspec(variance.model = list(model = "fGARCH", submodel = "TGARCH",

                                             garchOrder = c(1, 1)), 

                       mean.model = list(armaOrder = c(0, 0), archm = T), distribution.model = "snorm")

dopasGarch <- ugarchfit(spec = mojGarch, data = stopaZwrotu, out.sample = 0)

print(dopasGarch)

*---------------------------------*
*          GARCH Model Fit        *
*---------------------------------*

Conditional Variance Dynamics 	
-----------------------------------
GARCH Model	: fGARCH(1,1)
fGARCH Sub-Model	: TGARCH
Mean Model	: ARFIMA(0,0,0)
Distribution	: snorm 

Optimal Parameters
------------------------------------
        Estimate  Std. Error   t value Pr(>|t|)
mu     -0.011509    0.000678   -16.983        0
archm   1.029024    0.057292    17.961        0
omega   0.000539    0.000038    14.082        0
alpha1  0.041037    0.003865    10.618        0
beta1   0.922511    0.000036 25297.879        0
eta11   1.000000    0.182817     5.470        0
skew    1.161197    0.095820    12.118        0

Robust Standard Errors:
        Estimate  Std. Error   t value Pr(>|t|)
mu     -0.011509    0.000354   -32.488        0
archm   1.029024    0.023033    44.677        0
omega   0.000539    0.000018    30.293        0
alpha1  0.041037    0.001523    26.947        0
beta1   0.922511    0.000050 18517.286        0
eta11   1.000000    0.075490    13.247        0
skew    1.161197    0.089539    12.969        0

LogLikelihood : 902.5 

Information Criteria
------------------------------------
                    
Akaike       -5.9702
Bayes        -5.8838
Shibata      -5.9713
Hannan-Quinn -5.9356

Weighted Ljung-Box Test on Standardized Residuals
------------------------------------
                        statistic p-value
Lag[1]                     0.1093  0.7409
Lag[2*(p+q)+(p+q)-1][2]    0.5386  0.6758
Lag[4*(p+q)+(p+q)-1][5]    1.9115  0.6395
d.o.f=0
H0 : No serial correlation

Weighted Ljung-Box Test on Standardized Squared Residuals
------------------------------------
                        statistic p-value
Lag[1]                      1.715  0.1903
Lag[2*(p+q)+(p+q)-1][5]     2.352  0.5379
Lag[4*(p+q)+(p+q)-1][9]     3.638  0.6506
d.o.f=2

Weighted ARCH LM Tests
------------------------------------
            Statistic Shape Scale P-Value
ARCH Lag[3]    0.7304 0.500 2.000  0.3928
ARCH Lag[5]    1.2072 1.440 1.667  0.6726
ARCH Lag[7]    2.2430 2.315 1.543  0.6659

Nyblom stability test
------------------------------------
Joint Statistic:  1.287
Individual Statistics:              
mu     0.11514
archm  0.10348
omega  0.08008
alpha1 0.06191
beta1  0.06585
eta11  0.08665
skew   0.19526

Asymptotic Critical Values (10% 5% 1%)
Joint Statistic:     	 1.69 1.9 2.35
Individual Statistic:	 0.35 0.47 0.75

Sign Bias Test
------------------------------------
                   t-value   prob sig
Sign Bias           0.3681 0.7131    
Negative Sign Bias  1.3763 0.1698    
Positive Sign Bias  1.1213 0.2631    
Joint Effect        3.1698 0.3662    


Adjusted Pearson Goodness-of-Fit Test:
------------------------------------
  group statistic p-value(g-1)
1    20     14.67       0.7435
2    30     26.80       0.5825
3    40     31.47       0.7990
4    50     44.00       0.6756

Na pierwszy rzut oka może się wydać dziwne, że niewarunkowa średnia stopa zwrotu jest ujemna (mu = -0.0115), ale trzeba pamiętać, że model zawiera dodatkowy element - średnią warunkową zależną od warunkowego odchylenia standardowego i jej parametr jest dodatni (archm = 1,029). Powoduje to, że średnia stopa zwrotu zmienia się w czasie. Warto odnotować, że taki efekt może wcale nie zostać wykryty przez testy stabilności. 

Aby zobaczyć czy rozkład się zgadza, można użyć komendy

plot(dopasGarch, which=8)

i dodatkowo

plot(dopasGarch, which=9)

Wykonujemy prognozę. Zauważmy, że w tym przypadku możemy nieco poprawić precyzję prognozowanej stopy zwrotu: nie jest to po prostu wyraz wolny (średnia niewarunkowa), ale funkcja ryzyka (wariancji warunkowej). Z tego powodu wyłuskamy z empirycznego modelu nie tylko estymację ryzyka z próby, ale też "prognozy" (oczekiwanej stopy zwrotu) z próby. Prognozy poza próbą na 1 dzień do przodu także zrobimy.

# prognoza w próbie (dopasowanie do próby) 

stopaZwrotuDopas <- fitted(dopasGarch)

ryzyko <- sigma(dopasGarch)

# prognoza poza próbą

ileDoPrzodu <- 1

prognozaGarch <- ugarchforecast(dopasGarch, n.ahead = ileDoPrzodu)

prognozaStopaZwrotu <- fitted(prognozaGarch)

prognozaRyzyko <- sigma(prognozaGarch)

# zamiana na ts i łączenie z prognozą dla wykresu

stopaZwrotuWykres <- as.ts(stopaZwrotu)

stopaZwrotuDopasWykres <- as.ts(stopaZwrotuDopas)

ryzykoWykres <- as.ts(ryzyko)

ostatniOkres <- end(stopaZwrotuWykres)

dlugoscProby <- length(stopaZwrotuWykres)

stopaZwrotuWykres <- ts(c(as.numeric(stopaZwrotuWykres), rep(NA, ileDoPrzodu)), start = start(stopaZwrotuWykres))

stopaZwrotuDopasWykres <- ts(c(stopaZwrotuDopasWykres, rep(NA, ileDoPrzodu)), start = start(stopaZwrotuWykres))

prognozaStopaZwrotu <- ts(c(rep(NA, dlugoscProby-1), stopaZwrotuDopasWykres[dlugoscProby], 

                            as.numeric(prognozaStopaZwrotu)), start = stopaZwrotuWykres)

ryzykoWykres <- ts(c(ryzykoWykres, rep(NA, ileDoPrzodu)), start = start(stopaZwrotuWykres))

prognozaRyzyko <- ts(c(rep(NA, dlugoscProby-1), ryzykoWykres[dlugoscProby], as.numeric(prognozaRyzyko)), start = stopaZwrotuWykres)

okres <- tail(plik$Data[-1], Obs)

okresPrognoza <- seq.Date(from=max(okres), by="day", length.out=2)[-1]

okresWykres <- c(okres, okresPrognoza)

# wykres

Ost <- 15

zakresX <- c(okresWykres[dlugoscProby - Ost + 1], okresWykres[length(okresWykres)])

zakresY <- c(min(na.omit(stopaZwrotuWykres), -na.omit(ryzykoWykres)), max(na.omit(stopaZwrotuWykres), -na.omit(ryzykoWykres)) + max(na.omit(stopaZwrotuWykres), -na.omit(ryzykoWykres)))

plot(x=okresWykres, y=stopaZwrotuWykres, main="Dzienna stopa zwrotu WIG20", xaxt="n", xlim=zakresX, ylim=zakresY, lwd=2, type="l", xlab="")

axis(side=1, at=okresWykres, labels=okresWykres, las=2, cex.axis=0.8)

lines(x=okresWykres, y=stopaZwrotuDopasWykres, col="lightblue", lwd=2)

lines(x=okresWykres, y=prognozaStopaZwrotu, lwd=2, col="green")

lines(x=okresWykres, y=ryzykoWykres, lwd=2, col="red")

lines(x=okresWykres, y=-ryzykoWykres, lwd=2, col="red")

lines(x=okresWykres, y=prognozaRyzyko, lwd=2, col="brown")

lines(x=okresWykres, y=-prognozaRyzyko, lwd=2, col="brown")

abline(h=0, col="grey")

legend(x="topleft", legend=c("stopa zwrotu", "modelowana stopa zwrotu (GARCH-In-Mean)", "prognoza stopy zwrotu", "modelowane ryzyko (T-GARCH)", 

                             "prognoza ryzyka (T-GARCH)"), lwd=c(2,2,2,2,2), col=c("black",

                                                                       "lightblue",

                                                                       "green",

                                                                       "red",

                                                                       "brown"))

Miesięczne stopy zwrotu

Aby zagregować dane dzienne do miesięcznych użyłem pakietu xts. Obserwacji jest tak samo 300, więc cofamy się znacznie dalej w przeszłość. Zakres to lipiec 1999 - czerwiec 2024.

tabela <- as.data.frame(to.monthly(as.xts(plik), indexAt="endof", OHLC=FALSE))

cena <- tabela$Zamkniecie

Obs <- 300

stopaZwrotu <- tail(diff(log(cena)), Obs)

okres <- as.Date(tail(rownames(tabela)[-1], Obs))

Tym razem lepsze rezultaty daje EGARCH:

mojGarch <- ugarchspec(variance.model = list(model = "eGARCH", submodel = NULL,

                                             garchOrder = c(1, 1)), 

                       mean.model = list(armaOrder = c(0, 0), archm = T), distribution.model = "snorm")

I dalej już analogicznie do dziennych. Jedyną różnicą w kodzie będzie zastąpienie funkcji "day" przez "month":

okresPrognoza <- seq.Date(from=max(okres), by="month", length.out=2)[-1]

Częściowy wydruk:

Robust Standard Errors:
        Estimate  Std. Error  t value Pr(>|t|)
mu     -0.046871    0.002481 -18.8899 0.000000
archm   0.740374    0.038708  19.1271 0.000000
omega  -0.340842    0.042694  -7.9834 0.000000
alpha1 -0.081079    0.021606  -3.7526 0.000175
beta1   0.938421    0.007192 130.4857 0.000000
gamma1  0.129712    0.038211   3.3946 0.000687
skew    0.840676    0.063438  13.2519 0.000000

I wykresy

W pełnej skali analizowanego okresu dostaniemy następującą grafikę:

Obecnie mamy do czynienia ze spadającą zmiennością. Nie jest to przypadek, a zjawisko związane z grupowaniem wariancji. Po okresie dużej zmienności przychodzi mała (w podsumowaniu wyjaśnienie możliwej przyczyny).  Z tego powodu model prognozuje spadek stopy zwrotu w lipcu, a nawet indeksu. Nie podaję wartości, bo to nie ma większego sensu - widzimy, że nie jest to prawdziwa prognoza, tylko wartość oczekiwana, średnia. 

Podsumowanie

W ramach podsumowania oto wnioski i przemyślenia:

1. dla dziennych i miesięcznych stóp zwrotu WIG20 występuje efekt GARCH(1, 1). Dla ostatnich 300 dziennych lepszy jest TGARCH, dla ostatnich 300 miesięcznych EGARCH. Nie jest to przypadek. TGARCH lepiej radzi sobie z asymetrią wpływu pozytywnych i negatywnych informacji. Jak łatwo się domyślić, powinno (i jest) to bardziej widoczne dla zmian krótkoterminowych, bo wiadomości zmieniają się z dnia na dzień. Z kolei EGARCH będzie lepszy tam gdzie ujawnia się zjawisko grupowania wariancji. To bardziej tajemnicza sprawa, jak sądzę jest związana z cyklicznością przepływu kapitału. Kasa przecież generalnie spływa co miesiąc do gospodarki, a kalendarz wszyscy mają mniej więcej taki sam. Więcej kapitału to większa liczba inwestorów, to większa liczba wycen, a co za tym idzie większa rozbieżność opinii, stąd większa zmienność. Stąd oczywiste, że zjawisko grupowania wariancji prędzej będzie się odbywać w interwałach miesięcznych niż dziennych.  

2. GARCH stwierdza, że zarówno dzienne, jak i miesięczne stopy zwrotu WIG20 nie zawierają autokorelacji, natomiast korelują dodatnio z ryzykiem, tj. mamy do czynienia z GARCH-in-Mean. To dobra wiadomość dla teoretyków finansów, bo po pierwsze w końcu mamy dowód, że CAPM na polskim rynku działa oraz zachowana zostaje jego efektywność (bo właśnie nie ma autokorelacji, a jest dodatni związek między ryzykiem a oczekiwaną stopą zwrotu).

3. Chociaż zdecydowanie należy odrzucić rozkład normalny, to dla log-stóp zwrotu można spokojnie przyjąć skośno-normalny.

4. Biorąc pod uwagę poprzednie punkty, należy stwierdzić że mamy do czynienia z warunkowym CAPM ze skośnością oraz efektami GARCH.

P. S. Jeżeli test Nybloma wskazuje , że model jest niestabilny i poprawianie założeń tego nie zmienia, należy skorzystać z tych testów. Alternatywą jest jeszcze CUSUMQ lub ogólniejsza rodzina testów fluktuacji (dla kwadratów stopy zwrotu), które w pewnym sensie łączą warunkowe i niewarunkowe miary.