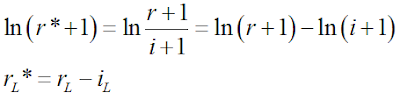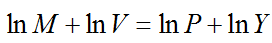Czy FED powinien podnieść stopy? Dynamiczna reguła Taylora mówi jasno

W ostatnich miesiącach inflacja w USA przekroczyła prawie trzykrotnie cel inflacyjny FEDu, co przypomina sytuację Polski. Cel inflacyjny to 2%, a zanotowane w czerwcu CPI wyniosło 5,4% (źródło: OECD). W maju było to 5%. Sytuacja więc lustrzana do Polski. I podobnie stopy procentowe są bliskie zera. 

Powstaje naturalne pytanie czy USA powinno podnieść stopy w obecnej sytuacji. Pewne jest, że władze FEDu zastanawiają się nad tym ruchem, jednak powstrzymują się z dwóch powodów. Pierwszy to uznanie, że obecna nadwyżka jest po prostu kompensatą za inflację poniżej celu w latach 2013-2016. Drugi to założenie, że obecna inflacja ma charakter przejściowy, stanowiąc szok podażowy spowodowany lockdownami na całym świecie. U nas podobnie się tłumaczą. 

To mnie zupełnie nie przekonuje, bo po pierwsze warto przypomnieć skutek szoku podażowego w latach 70 zeszłego wieku, gdy państwa OPEC ucięły dostawy ropy na Zachód. Niektórzy ekonomiści porównują ze sobą tamto wydarzenie i dzisiejsze lockdowny, wieszcząc potężny kryzys (zob. artykuł na interii: Matka wszystkich kryzysów). Po drugie w wielu krajach Europy, np. Francji, Niemczech i UK, również inflacja była niska w poprzednich latach, a dzisiaj też nie jest wysoka. W końcu po trzecie zawsze można obniżyć z powrotem stopy, gdyby rzeczywiście sytuacja się poprawiła.

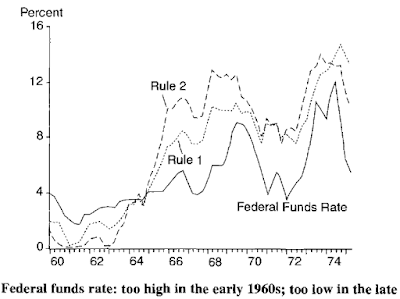
Jest jednak pewna różnica między FED a NBP. W tym pierwszym zarządzają profesjonaliści. Wiadomo na przykład, że FED stosuje regułę Taylora, a przynajmniej podejmuje decyzje mając ją na względzie. Możemy wejść na stronę ich blogu, aby obserwować bieżące odchylenia efektywnej stopy funduszy federalnych od tej reguły:

Rysunek 1

Linia niebieska wskazuje stopę procentową zgodnie z regułą Taylora, a linia czerwona rzeczywistą stopę.

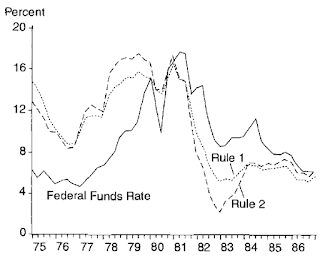
Przybliżmy ostatnie 20 lat:

Rysunek 2

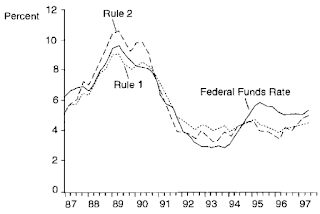
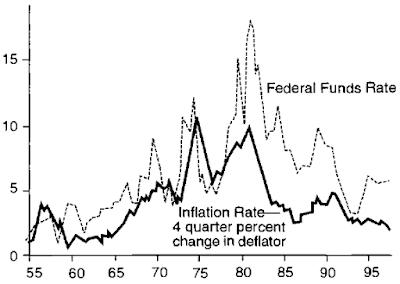
Gdyby FED stosował się zgodnie z regułą, można by ograniczyć kryzys z 2007. Nie powstrzymałoby go zapewne, ale jego siła byłaby mniejsza. Zastanawiające jest dlaczego FED już długo po tym kryzysie utrzymywał stopy na poziomie bliskim zera prosząc się o kolejny krach? Odpowiedzią okazuje się luka PKB - FED również publikuje dane o niej. Dopóki luka była ujemna, FED mógł bezpiecznie utrzymywać niskie stopy: 

Rysunek 3

Powstaje tu jednak pewien zgrzyt. Bo w regule Taylora ujemna luka obniża docelową stopę. Jednocześnie w czasie pokryzysowym inflacja była poniżej docelowego poziomu 2%, co również obniża docelową stopę. W jaki więc sposób reguła kazała przyjąć w tym okresie poziom 2%? Problem polega na tym, że na pierwszym wykresie widzieliśmy oryginalną formułę Taylora, w której przyjęto wzrost potencjalnego PKB na poziomie 2%. Z kolei drugi wykres wskazuje różnicę między faktycznym PKB a potencjalnym PKB, który nie rośnie w stałym tempie, a obliczony zgodnie z pewnym modelem. No właśnie, ale jakim modelem? 

Aby znaleźć odpowiedź na to pytanie, sięgnąłem do dokumentu opracowanego przez CBO (Congressional Budget Office). Na str. 33 jest grafika, która pomaga zrozumieć budowę modelu (wzrostu) potencjalnego PKB:

Rysunek 4

Mówiąc w skrócie potencjalny wzrost gospodarczy na Rysunku 4 został oszacowany jako suma wzrostu potencjalnej siły roboczej (kolor czarny) oraz wzrostu produktywności pracy (pomarańczowy). Dlaczego tak? Przypomnijmy, że PKB rośnie w tempie potencjalnego PKB, jeśli czynniki wytwórcze pracują na maksymalnym poziomie (zob. wpis). W praktycznym sensie oznacza to, że bezrobocie i stopa procentowa znajdują się na swoich naturalnych poziomach (zob. wpis). Naturalna stopa zatrudnienia, czyli jakby przeciwieństwo naturalnej stopy bezrobocia, będzie więc odpowiadać kolorowi czarnemu, a naturalna stopa procentowa - kolorowi pomarańczowemu. Warto przypomnieć, że ta ostatnia stanowi krańcową produktywność kapitału (zob. wpis), czyli też kapitału ludzkiego.

Widzimy, że potencjalny PKB rośnie coraz wolniej. W latach 2008-2018 wzrost wyniósł średniorocznie 1,6%, czyli mniej niż założone przez Taylora 2%. W latach 2019-2023 ma to być 2,1%, a w kolejnych znowu spaść do 1,8%.

FED publikuje wszystkie potrzebne dane, a więc nie tylko o stopach i faktycznym PKB, ale też potencjalnym PKB. Wobec tego przeprowadziłem analizę, zgodnie z którą stworzyłem dynamiczną regułę Taylora dla USA, którą porównałem ze statyczną wersją. Naturalną stopę procentową oszacowałem jako wzrost potencjalnego PKB per capita. Wzrost populacji wpływa bowiem na potencjał gospodarki, ale nie na jej produktywność. W ten sposób wyeliminowałem kolor czarny z Rysunku 4. Można się zastanowić czy nie powinienem podzielić potencjalnego PKB przez wielkość zatrudnienia zamiast całą ludność. Ale przecież wzrost niepracujących też zwiększa pośrednio potencjał PKB, ponieważ rośnie konsumpcja. A naturalna stopa procentowa nie zależy od konsumpcji, tylko inwestycji. Oczywiście obydwie wielkości są od siebie zależne, ale należy tu patrzeć bardziej od strony podażowej niż popytowej. Stąd dzielimy przez całą populację.

W sumie stworzyłem dynamiczny model Taylora. Porównujemy dane bieżące do poprzedniego roku:

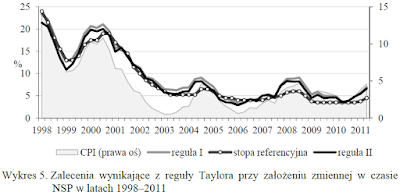
Rysunek 5

Kolor czerwony - Dynamic Taylor rule, czyli dynamiczna reguła Taylora;

Fioletowy - Taylor rule, czyli klasyczna, statyczna reguła Taylora;

Zielony - efektywne stopy procentowe funduszy federalnych.

Rysunek 5 jest identyczny jak Rysunek 1, z tą różnicą, że dodałem model dynamiczny. Zwróćmy uwagę, że w latach 2003-2006 FED zaniżał stopę średnio o 1,6 pkt proc. W czasach kryzysu 2007-2009 FED już stosował prawidłowo regułę. Okres 2010-2015 skorygowana reguła znajduje się bliżej rzeczywistych stóp niż wskazuje klasyczna. Potwierdza to opinię, że regułę Taylora należało skorygować.

Jakie to ma wnioski na dziś? Otóż sytuacja wygląda tak, że stopa FED wynosi 0,08%, podczas gdy klasyczna reguła Taylora każe ją ustawić na 2,51%, a dynamiczna reguła Taylora - na 1,88%. Tak więc statyczna metoda zawyża stopę 0,6 pkt. proc., ale FED zaniża ją o 1,8 pkt proc. Oto tabela od 2015:

 Zatem FED powinien natychmiast podnosić stopy, a nie czekać na inflacyjne tsunami. Może pomogłoby to ocknąć się też NBP.

Link do całej analizy znajduje się tutaj.

Źródło danych:

https://fred.stlouisfed.org/

Widmo 20-procentowej inflacji powraca

Może to się wydaje kuriozalne i abstrakcyjne, ale są dwie przesłanki, które wskazują, że może nas czekać gigantyczna, 20-procentowa inflacja. Pierwszą przedstawiłem rok temu (wpis Czy powinniśmy przygotować się na inflację rzędu 20%? ). W czasach grypy hiszpanki i po niej w USA panowała wielka inflacja i I Wojna Św. była tylko częściową przyczyną. W roku 1918 średnie CPI wyniosło 18%, w 1919 14,6%, w 1920 15,6%. Gdyby jednak stopy procentowe były w tym czasie wyższe, to prawdopodobnie udałoby się uniknąć takich podwyżek cenowych. Krótkoterminowa (roczna) rentowność obligacji skarbowych wynosiła w 1918 5,2%, w 1919 5,5%, w 1920 6,2%. Dane można obejrzeć na tej stronie. 

Gdyby jednak tylko na tej jednej przesłance poprzestać, to i tak nie było tak źle, bo w kolejnych latach nastąpiła deflacja zrównująca poprzednie sztuczne podwyżki.

Druga przesłanka wynika wprost z reguły Taylora, którą prezentowałem w poprzednim artykule. Mamy więc formułę:

r = i + r* + 0,5 (i - i*) + 0,5 (y - y*)

gdzie:

r - nominalna (logarytmiczna) stopa procentowa, jaką bank centralny powinien przyjąć;

i - (logarytmiczna) stopa inflacji;

r* - realna (logarytmiczna) naturalna stopa procentowa, którą utożsamiłem ze średnią stopą wzrostu realnego PKB per capita;

i* - oczekiwana (logarytmiczna) stopa inflacji lub cel inflacyjny;

y - (logarytmiczna) stopa wzrostu realnego PKB.

y* - (logarytmiczna) stopa wzrostu potencjalnego realnego PKB w stosunku do faktycznego realnego PKB. 

Dla uproszczenia założymy, że w poprzednim okresie PKB był równy potencjalnemu PKB, tj. r* = y*:

r = i + y* + 0,5 (i - i*) + 0,5 (y - y*)

Normalnie formułę stosuje się w celu uzyskania r, a więc gdy podstawimy za i = 5%, y* = 4%, i* = 2% oraz y = 1% (bieżąca estymacja GUS mówi o spadku 1,4% w 1 kwartale tego roku, ale w kolejnych kwartałach prognozuje się odbicie), to dostaniemy:

r = 5 + 4 + 0,5*(5 - 2) + 0,5*(1 - 4) = 9%

To teraz zróbmy na odwrót: skoro NBP i RPP ustawiają stopy na zero, to sprawdźmy jaki mają faktyczny cel inflacyjny. Za r podstawimy 0 i poszukujemy i*:

0 = 5 + 4 + 0,5*(5 - i*) + 0,5*(1 - 4)

Stąd

i* = 20.

Zatem w dzisiejszych okolicznościach celem inflacyjnym banku centralnego jest galopująca inflacja rzędu 20%.

Ktoś mógłby mieć wątpliwości, czy rzeczywiście w drugą stronę to tak działa. Trzeba pamiętać, że formuła Taylora została wyprowadzona z teorii optymalnego zachowania. Jeżeli przyjąć, że cel inflacyjny wynosi 20%, to teraz podstawiając do formuły dostaniemy rzeczywiście r = 0%. Przecież formuła wskazuje właśnie ile powinna wynieść stopa %, aby uzyskać cel inflacyjny. Tak więc podstawienie, jakiego dokonałem nie jest odwróceniem przyczyny i skutku.

Druga wątpliwość jaka może się nasunąć, to wartości zmiennych. Np. można zmniejszyć y* do 3%. To jednak niewiele zmienia, bo wtedy uzyskamy inflację 19%. Trzeba też zauważyć, że y = 1% jest i tak pesymistyczne, bo banki podnoszą prognozy na 2021 aż do 5% (np. zob. tu).  A wtedy inflacja wzrosłaby - przy zał. y* = 4% - do 24%, a przy zał. y* = 3% - do 23%. To co tu piszę nie jest jakąś abstrakcją, to jest ostrzeżenie przed nieodpowiedzialną polityką zerowych stóp.

Wicksell spotyka Taylora - czyli ile dziś powinna wynosić stopa procentowa?

W literaturze ekonomicznej znana jest tzw. reguła Taylora, czyli reguła optymalizująca politykę monetarną. Ma ona postać:

(1)

gdzie:

r - nominalna (logarytmiczna) stopa procentowa, jaką bank centralny powinien przyjąć;

i - (logarytmiczna) stopa inflacji;

r* - realna (logarytmiczna) stopa w równowadze, Taylor [5] zaproponował, aby równała się 2%;

i* - oczekiwana (logarytmiczna) stopa inflacji lub cel inflacyjny. Taylor ustawił ją na 2%;

y - (logarytmiczny) poziom realnego PKB;

y* - (logarytmiczny) poziom potencjalnego PKB;

a, b - współczynniki. Taylor na podstawie badań zaproponował aby a = b = 0,5. 

 

Reguła Taylora nie jest regułą, którą sobie Taylor wymyślił, bo ma teoretyczną podbudowę, chociaż w jego oryginalnym artykule nie znalazłem wyprowadzenia. Natomiast znalazłem je w [3, 4]. 

Jeżeli inflacja jest równa celowi inflacyjnemu oraz gdy luka PKB nie występuje, to reguła Taylora sprowadza się do prostej sumy naturalnej stopy  procentowej oraz stopy inflacji. W tym miejscu mała uwaga. Zwróćmy uwagę, że dostaliśmy nominalną stopę, a przecież zgodnie z tym art. jest ona równa: r* (1 + i) + i.  Skąd ta różnica? Otóż tutaj operujemy logarytmicznymi stopami. W Dodatku nr 1 pokazałem, że po przekształceniu w logarytmy wszystko się zgadza.

Zauważmy, że y i y* są to poziomy, a nie stopy wzrostu PKB. Uzyskanie samego potencjalnego PKB może być trudne. Problem ten można rozwiązać używając zamiast poziomów zmian w czasie. Ponieważ y - y* jest po prostu luką PKB, to, możemy w ich miejsce wstawić:

- za y: bieżące czy oczekiwane tempo wzrostu realnego PKB, tj. y2 - y1

- za y*: tempo wzrostu potencjalnego PKB nie w stosunku do poprzedniego poziomu, tylko w stosunku do realnego PKB. Jeżeli uznamy, że w poprzednim okresie PKB znajdował się w równowadze, czyli był równy potencjalnemu PKB z tamtego okresu, to otrzymamy rzeczywiście tempo potencjału. Czyli zamiast y* wpiszemy y* - y1.

Wtedy razem będziemy mieć (y2 - y1) - (y* - y1) = y2 - y*. Czyli wychodzi to co być powinno zgodnie z regułą Taylora. Stąd wystarczy znajomość po pierwsze faktycznej zmiany (y2 - y1) oraz po drugie teoretycznej zmiany z y1 na y*.  

Aby nie komplikować zbytnio zapisów, dalej będę używał zapisów:

y - (logarytmiczna) stopa wzrostu realnego PKB;

y* - (logarytmiczna) stopa teoretycznego wzrostu realnego PKB (potencjalnego PKB w stosunku do poprzedniego poziomu faktycznego PKB).

Miejmy na względzie, że to ostatnie nie oznacza trendu PKB ani średniego potencjalnego wzrostu, tylko zmianę z tego co było na to co powinno być.

Z poprzednich analiz wiemy, że stopa % w równowadze (gdy inwestycje są równe oszczędnościom) stanowi stopę wzrostu PKB z inwestycji. W kategoriach realnych możemy ją utożsamić z Wicksellowską naturalną stopą procentową. Wiemy, że ta stopa stanowi krańcową produktywność kapitału i jest całkowicie niezależna od inflacji. W sumie r* będzie stanowić inwestycyjną część wzrostu potencjalnego PKB. Równanie (1) możemy więc zapisać:

(2)

gdzie c to współczynnik.

Potencjalny PKB rośnie w czasie  nie tylko dzięki inwestycjom, ale też dzięki konsumpcji. Na rynkach rozwiniętych, konsumpcja będzie rosła już tylko dzięki rosnącej populacji. Jeśli wzrost gospodarczy będziemy mierzyć na osobę, to wyeliminujemy ten wpływ. Zatem inwestycje generują cały potencjalny wzrost, tj. c = 1:

(3)

Przyjmijmy tak jak Taylor [5], że a = b = 0,5:

(4)

Przykłady

Powiedzmy, że PKB rośnie zgodnie z potencjalnym PKB, tj. y = y*: 

(5)

Powiedzmy, że inflacja wynosi 5%, a celem jest 2%. Wtedy bank centralny powinien zastosować formułę

r = 0,05 + y* + 0,5*(0,05 - 0,02) = y* + 0,065. 

dzięki której obniży inflację do 2%.

Czyli jeżeli potencjalny wzrost wynosi 0%, to stopa procentowa powinna wynieść aż 6,5%. Jeśli przyjąć, że y* = 2%, to r powinna wynieść 8,5%.

Następnie załóżmy, że bank centralny jednak chce, aby inflacja wyniosła 5%:

r = 0.05 + y*.

To samo osiągnęlibyśmy, gdyby zamiast celu  inflacyjnego 5% współczynnik a równałby się zero. W każdym razie widzimy, że optymalna stopa procentowa powinna być równa stopie inflacji powiększonej o realny wzrost potencjalnego PKB.

Powiedzmy następnie, że chociaż ceny rosną zgodnie z oczekiwaniami, to PKB rośnie w innym tempie niż potencjał. Zgodnie z równaniem (4) otrzymamy:

 Jeśli y = 5%, a y* = 2%, to NBP razem z RPP powinien kierować się powyższą formułą, otrzymując:

r = 0.05 + 0.02 + 0,5*0,03 = 8,5%. 

W końcu możemy połączyć wszystkie zmiany razem - inflację i PKB, aby oszacować prawidłową stopę. W 2020 Polska zanotowała inflację 3,4%, a realny PKB w 2020/2019 spadł o ok. 2,8% (źródło). Jeśli założyć w uproszczeniu, że średnia wzrostu stanowi y*, to wg GUS od 1995 r. będzie to 4% rocznie. Cel inflacyjny to 2%. Podstawiamy do (4):

r = 3,4 + 4 + 0,5*(3,4 - 2) + 0,5*(-2,8 - 4) = 4,7. 

Gdyby tym krajem rządzili ludzie kompetentni, to w 2020 powinniśmy mieć stopę referencyjną na poziomie 4,7%, gdyż to pozwoliłoby obniżyć inflację do 2%. Natomiast przy dzisiejszej inflacji 5% i wzroście 1% PKB (mniej więcej tyle jest obecnie):

r = 5 + 4 + 0,5*(5 - 2) + 0,5*(-1,4 - 4) = 7,8.  

Z dzisiejszej perspektywy 8% to szokująco wysoko, ale to pokazuje do jakich poziomów się przyzwyczailiśmy.

Wg mojego poglądu cel inflacyjny to powinien być 0-1%. A to oznacza, że gdybym odpowiadał za politykę monetarną ustawiłbym stopę na poziomie ok. 9%.

Badania empiryczne

No dobrze, ale jak to wygląda w innych krajach? Czy inni stosują tę regułę? Taylor w kolejnym artykule [6] zbadał na ile polityka FED odchyla się od jego reguły w różnych okresach, kiedy nie była jeszcze znana.

Tutaj kolejna uwaga. Newralgicznym punktem są wielkości współczynników, dlatego autor porównał dwie reguły z faktyczną polityką pieniężną FEDu. Pierwsza reguła przyjmuje a = b = 0,5, natomiast druga a = 0,5 oraz b = 1. Czyli druga eliminuje y* z równania (3).

 Lata 1960-1974: Wg obydwu reguł w 1 połowie lat 60 r było za wysokie, a w kolejnych latach do połowy lat 70 za niskie.

Lata 1975 - 1986: Pierwsza połowa tego okresu to polityka zbyt niskich stóp i druga połowa to okres za wysokich stóp

Lata 1987-1997: do połowy okresu polityka FED się pokrywała ze średnią regułą (średnia z obydwu reguł), następnie w połowie czasu r była za niska, by w końcowej fazie znowu być za wysoka.

 

Taylor pokazał też jak kształtowała się inflacja na tle stopy % w całym badanym okresie:

Lata 70-te i 80-te to był okres dużej inflacji, a więc FED popełnił błędy wtedy. Rzeczywiście reguła Taylora nakazywała dużo wyższe poziomy stóp. Już w drugiej połowie lat 60-tych inflacja podchodziła do 5% i już wtedy FED powinien podwyższyć stopy o ok. 6 pktów proc. Był to błąd, który kosztował USA w kolejnych latach 10% inflacji. 

U nas niestety może być podobnie. Jeśli nie przejmą władzy odpowiedzialni ludzie, to może naprawdę dojść do katastrofy.

Na rynkach rozwijających się potencjalny PKB będzie rósł coraz wolniej, tak że y* będzie malał w czasie (tzn. naturalna stopa procentowa spada). Ta sytuacja dotyczy Polski i dlatego badanie reguły Taylora powinno uwzględniać te zmiany. Tego dokonała A. Michałek [1], która w badaniu na latach 1998-2011 przedstawia następujący wykres:

 Jak widać stopa referencyjna ustanowiona przez NBP była przez większość czasu zgodna z regułą Taylora I i II, dostosowując się odpowiednio do inflacji.

Są jednak nowsze badania, obejmujące okres rządów PIS. P. Błaszczyk [2] również szacuje zmienną naturalną stopę do porównania reguły Taylora (w dwóch wariantach) z polityką NBP. Oto wykres:

 

gdzie:

RT (0,5) - reguła Taylora dla a = 0,5, 

RT (0,75) - reguła Taylora dla a = 0,75.

Do roku 2015 polityka NBP była całkiem racjonalna, podążała mniej więcej za optimum. Ponieważ stopa nie powinna być ujemna, to duże odchylenie w 2015 i 2016 należy do kategorii tzw. pułapki płynności (prowadzi do deflacji). Co się dzieje po roku 2015? NBP nie robi kompletnie nic mimo że deflacja już dawno się skończyła. Zauważmy, że przed 2015 stopy często  się zmieniały, dostosowując się do koniunktury, a po 2015 nie ma kompletnie żadnej reakcji. Pytanie więc za co podatnik płaci im grube pieniądze? Ale to jeszcze nic, bo nierobienie niczego jest lepsze niż robienie czegoś szkodliwego. A z tym mieliśmy do czynienia w 2020. Błaszczyk tak to komentuje (str. 80-81):

Najbardziej kontrowersyjna sytuacja pojawiła się jednak na początku 2020 r. Inflacja przekroczyła górną granicę docelowego pasma. W takich okolicznościach reguła Taylora wskazuje na potrzebę znacznego podniesienia stopy procentowej. Tymczasem RPP podjęła w marcu, kwietniu i maju trzy decyzje obniżające stopy procentowe, w tym ostatecznie stopę referencyjną do wartości 0,1%. Stopa w ujęciu realnym, w obliczu wysokiej stopy inflacji, spadła znacznie poniżej zera.

Dodatek nr 1.

Kiedyś pokazałem, że realna stopa procentowa wyraża się wzorem:

Dodajmy 1 do obu stron:

Zlogarytmujmy strony:

Tak więc logarytmiczna realna stopa proc. (r_L*) jest równa różnicy między logarytmiczną nominalną stopą proc. (r_L) a stopą inflacji (i_L). Dlatego używanie logarytmów jest wyjątkowo wygodne.

Dodatek nr 2.

Przypomnę, że kiedyś wyprowadziłem równanie wymiany Fishera:

gdzie M - ilość pieniądza w obiegu, V - szybkość obiegu pieniądza, P - średnia cena, Y - średni dochód.

Logarytmując obie strony dostajemy:

(6)

Dla dwóch okresów będzie inny poziom tych zmiennych. Odejmujemy stronami i przekształcamy:

 

ostatnie równanie zapiszemy krócej:

 

 

Załóżmy, że firma bierze kredyt i bank zwiększa podaż pieniądza zaciągając na to pożyczkę w banku centralnym. Początkowo więc podaż pieniądza wzrasta o całą wielkość kredytu. Jednak na koniec okresu firma spłaca kredyt wraz z odsetkami. To znaczy, że sam kredyt nie zwiększył sumarycznie ilości pieniądza w gospodarce, bo wrócił do banku. Czyli to odsetki muszą ją zwiększyć. Ale żeby to było możliwe, to między początkiem a końcem okresu banki musiały zwiększyć podaż o nowy kredyt, który w pewnej części poszedł na te odsetki (można powiedzieć, że zrefinansowano kredyt). I to właśnie wyraża zmiana z M1 na M2. Ponieważ stopa procentowa wyraża procent pewnego kapitału w postaci odsetek, a ten kapitał równa się M, to możemy założyć, że cała zmiana z M1 na M2 równa się tym odsetkom. W takim razie zmiana ilości pieniądza odpowiada nominalnej stopie %, tj. r = m = ln(M2/M1). Jeżeli szybkość obiegu pieniądza byłaby stała w czasie, tj. v = 0, to dostajemy

(7)

tj. regułę Taylora, gdy bieżąca inflacja jest równa oczekiwanej inflacji (targetowi) oraz realny PKB jest równy potencjalnemu PKB (w sensie praktycznym - zob. ostatni wpis). Można powiedzieć, że wzór (7) wyraża regułę Wicksella, który właśnie postulował, by stopę procentową ustalać na takim poziomie jak wzrasta podaż pieniądza. Jest to po prostu naturalna stopa procentowa, będąca sumą stopy wzrostu realnego PKB oraz stopy inflacji.

Literatura:

[1] A. Michałek, Szacowanie naturalnej stopy procentowej dla Polski, 2012;

[2] Błaszczyk, P., Zmiany stopy procentowej Narodowego Banku Polskiego w XXI w. na tle reguły Taylora, 2020;

[3] Davis, C. et al., Deriving the Taylor Principle when the Central Bank Supplies Money, 2012;

[4] Piergallini, A., Rodano, G., A Simple Explanation of the Taylor Rule, 2016;

[5] Taylor, J. B., Discretion Versus Policy Rules in Practice, 1993;

[6] Taylor, J. B., Monetary Policy Rules, 1999.

Potencjalny PKB w ścisłym i praktycznym sensie

W takie upały ciężko się pisze, dlatego pokażę krótko, kiedy obniżanie / podnoszenie stóp procentowych jest szkodliwe dla gospodarki, a kiedy nie. Chociaż ostatnie tematy już poruszały tę kwestię, wskazując, jak zmiana stopy % wpłynie na inflację, to jednak pozostała niewyjaśniona do końca kwestia zależności stopy i PKB. A przecież we wpisie   Naturalna stopa procentowa - wstęp stwierdziłem, że optymalna stopa powinna stabilizować zarówno ceny, jak i PKB - dobrze będzie to usystematyzować.

PKB w ścisłym sensie

Dotychczas w uproszczeniu wykres podaży przedstawiałem jako linię prostą. W krótkim okresie była ta linia pionowa, przez którą przechodziła ujemnie nachylona linia popytu. Teraz jednak, aby zaakcentować występowanie potencjalnego PKB, podaż przed punktem tego potencjału będzie linią poziomą, a od tego punktu stanie się pionowa:

 
Rynek nr 1

Do pewnego poziomu firmy mogą bez żadnych kosztów zwiększać lub zmniejszać produkcję i stąd przesunięcie krzywej popytu nie zmienia ceny w tym obszarze. Przykładem jest rynek książek. Książki mogą być magazynowane w bibliotekach, dlatego jeśli popyt na nie wzrasta, to podaż szybko się dostosuje do popytu, jeżeli książki są w magazynach. 

Zaczynamy od p. A. Spadek stopy % spowoduje wzrost popytu na kredyty, następuje zwiększenie popytu konsumpcyjnego i inwestycyjnego - krzywa popytu się przesuwa w prawo z y1 do y2 i ustala się nowa równowaga w p. B. Od tego punktu podaż nie jest w stanie się zwiększać, dlatego każda dodatkowa obniżka stopy spowoduje, że producenci zaczną jedynie podnosić ceny. A więc wzrost popytu do y3 jest chwilowy (p. C): firmy reagują na nowy popyt podwyżkami cenowymi, a to obniża popyt z powrotem do poziomu y2. Mimo powrotu efekt niższej stopy pozostaje: nowa równowaga ustala się w p. D, gdzie są wyższe ceny i potencjalny PKB.

Ten potencjalny PKB możemy nazwać potencjalnym PKB w ścisłym sensie - podaż jest całkowicie sztywna i nie reaguje na zmiany popytu.

PKB w praktycznym sensie

W rzeczywistości przejście od linii poziomej do pionowej nie wygląda tak skrajnie. Powinniśmy uwzględnić stopniowe przejście do potencjalnego PKB. To przejście możemy nazwać potencjalnym PKB w sensie praktycznym. Spójrzmy na Rysunek nr 2.

Rysunek nr 2

 

Gdyby wziąć pierwszy i ostatni fragment tej krzywej dostalibyśmy Rysunek nr 1. Pośrednie fragmenty wskazują na występowanie takiego poziomu podaży, że podaż rośnie razem z ceną. 

Jednym z takich pośrednich punktów jest potencjalny PKB w sensie praktycznym. Są dwa sposoby na jego obserwację i prognozę inflacji. Pierwszy to stopa bezrobocia - jeżeli jest mniejsza od naturalnej (4-6%), to istnieje duże prawdopodobieństwo, że gospodarka przekroczyła potencjał, a jeżeli jest większa od naturalnej, to gospodarka znajduje się poniżej potencjału.  Drugi sposób to właśnie stopa procentowa - jeżeli jest poniżej naturalnej (tj. poniżej krańcowej produktywności gospodarki), to PKB rośnie powyżej potencjału w sensie praktycznym, a jeżeli powyżej naturalnej, to na odwrót. 

Przed wejściem podaży w obszar potencjału w sensie praktycznym, ceny rosną zgodnie z oczekiwaną inflacją, czyli np. 1-2% (obszar między p1 a p2). Po przekroczeniu tego obszaru, następuje wzrost samej inflacji. W efekcie ceny nie tylko rosną, ale rosną coraz szybciej. To dlatego zadaniem banku centralnego powinno być powstrzymanie popytu przed wejściem w ten obszar, ale jednocześnie zahamowanie zbytniego spadku poniżej tego obszaru. Do tego powinna służyć m.in. polityka stóp procentowych:

Polityka obecnych władz jest fatalna. NBP i RPP ustalając stopę referencyjną na poziomie 0% doprowadziły do najwyższej inflacji w UE (źródło) w 2020, a od 2021 rośnie ona powyżej 5% (źródło). 

Każdy dodatkowy impuls popytowy będzie powodował, że ceny będą jeszcze przyspieszać, a jednocześnie podaż będzie coraz wolniej odpowiadać. W końcu przestanie kompletnie reagować i każde przesunięcie krzywej popytu w prawo wywoła jedynie kolejny wzrost cen. Punkt, którego podaż nie jest w stanie osiągnąć, bo czynniki wytwórcze są ograniczone, staje się potencjalnym PKB w ścisłym sensie. Bezrobocie jest tutaj dosłownie zerowe. Ale nawet jeśli nie jest zerowe, to przynajmniej stopa procentowa jest zerowa. Chociaż pozornie wydaje się, że z taką sytuacją mamy do czynienia, to tak nie jest, bo o ile stopa referencyjna i redyskontowa są zerowe, to średnie RRSO na rynku już nie. Żeby RRSO osiągnęła 0, to po pierwsze ryzyko płynności klientów musiałoby też być zerowe, a po drugie użyteczność trzymania pieniądza, np. na przyszłą konsumpcję, musiałaby też być zerowa. Innymi słowy bank nie musiałby się obawiać, że klient nie spłaci kredytu, a dodatkowo większość ludzi wolałaby zawsze konsumpcję bieżącą od przyszłej. Są to założenia nierealne, dlatego rynkowa stopa % nigdy nie będzie zerowa. Można się nawet pokusić o tezę, że prędzej bezrobocie będzie zerowe niż rzeczywista stopa procentowa (jaki sens byłoby prowadzenie banku?).

Okres krótki czy długi?

Przedstawiona analiza nie dotyczy krótkiego okresu, ale każdego. Jest to istotna różnica w stosunku do poprzednich analiz, które stawiały nacisk na podział okresów na krótki i długi (zob. tu i tu). Należy pamiętać o względności czasu, bo część pionowa krzywej podaży w bardzo długim okresie będzie się nachylać albo przesuwać w poziomie, tak jak to opisywałem poprzednio. Na przykład 5 lat, które standardowo uznajemy za okres długi, będzie okresem krótkim w stosunku do 25 lat. Wraz ze wzrostem populacji lub postępem technicznym podaż zacznie absorbować popyt.

Naturalna stopa procentowa - czy Wicksell się mylił?

 W 1898 r. szwedzki ekonomista - Knut Wicksell - wydał Geldzins und Güterpreise (ang. Interest and Prices), w której zaproponował pojęcie naturalnej stopy procentowej (NSP). Rozdział 8 rozpoczyna się od jej definicji*:

Istnieje pewna stopa oprocentowania kredytów, która jest neutralna w odniesieniu do cen towarów, i nie ma tendencji ani do ich podnoszenia ani do ich obniżania. Jest to z konieczności to samo, co stopa która byłaby określona przez popyt i podaż, gdyby nie używano pieniądza, a wszystkie pożyczki byłyby udzielane w formie rzeczywistych dóbr kapitałowych.

 (przetłumaczono z www.DeepL.com/Translator (wersja darmowa))

Dalej wyjaśniony zostaje jej mechanizm (str. 103):

W teorii można założyć, że przedsiębiorca pożycza dobra konsumpcyjne od kapitalistów w naturze, a następnie wypłaca je w naturze w postaci płac i czynszów. Na koniec okresu produkcji spłaca pożyczkę z własnego produktu, bezpośrednio lub po wymianie na inne towary (przy czym zakłada się, że ceny względne pozostają niezmienione). Gdyby tę procedurę przyjęli wszyscy przedsiębiorcy, którzy pracują z pożyczonym kapitałem, konkurencja przyniosłaby pewną stopę procentową, która musiałaby być zapłacona kapitalistom w formie jakiegoś towaru lub innego dobra. Wysokość tej stopy procentowej byłaby określona przez "podaż i popyt" na kapitał. To sformułowanie mówi nam jednak bardzo niewiele. Ale można ustalić dla stopy procentowej górną granicę, która ma bardziej namacalne znaczenie. Tą wartością graniczną jest kwota, o którą produkt całkowity (lub jego ekwiwalent w innych towarach) przekracza sumę płac, czynszów itp. Wielkość tej nadwyżki zależy z jednej strony od produktywności przedsiębiorstwa, a z drugiej od poziomu płac i czynszów.

Przyjęcie modelu barteru do analizy ekonomicznej jest bardzo dobrym pomysłem, bo pozwala oddzielić sferę realną od pieniężnej. W ten sposób Wicksell dochodzi do wniosku, że NSP to krańcowa produktywność kapitału. 

Jeżeli wyprodukowanie dodatkowego produktu spowoduje, że zysk spadnie (z powodu nadmiernego kosztu) to tego produktu już nie należy produkować. Ale to znaczy, że przy nieco mniejszej produkcji, zysk jeszcze rósł (wraz ze wzrostem produkcji), czyli przychód rósł szybciej niż koszty. A to znaczy, że przychód z dodatkowego produktu był większy niż jego koszt. To musi znaczyć, że zysk przestaje rosnąć, gdy zwiększymy produkcję, a przychód z dodatkowej produkcji zrówna się z jej kosztem. To właśnie znaczy twierdzenie, że maksymalizacja zysku jest osiągnięta, gdy krańcowy przychód jest równy krańcowemu kosztowi (matematyczny opis w tym artykule). 

Załóżmy, że firma zaciąga kredyt w banku i z całego kredytu tworzy produkcję. To znaczy, że w tym kredycie siedzą wszystkie koszty operacyjne (czynniki wytwórcze). Odsetki jako koszt finansowy powstają dopiero na końcu cyklu produkcyjnego. Księgowo powstają dwa rodzaje kosztów: operacyjne (kredyt) oraz finansowe (odsetki), lecz ekonomicznie biorąc kosztem są tylko odsetki, ponieważ koszty operacyjne w całości zostają pokryte  kredytem.

Jeżeli podzielimy odsetki przez wielkość produkcji, to otrzymamy koszt jednostkowy albo inaczej koszt przeciętny. Dalej, jeden produkt jest jednocześnie dodatkową produkcją, czyli koszt krańcowy = zmiana odsetek / 1 produkt = zmiana odsetek. I teraz połączmy dwie rzeczy:

1) odsetki to koszt krańcowy;

2) warunek maksymalizacji zysków to równość przychodu krańcowego z kosztem krańcowym.

Dedukujemy, iż odsetki na jednostkę lub w krótkim okresie równają się krańcowemu przychodowi. 

Stopa procentowa to odsetki dzielone przez wielkość kredytu, a z powyższego wynika, że stopa procentowa = krańcowy przychód / kredyt. Innymi słowy stopa procentowa to krańcowa produktywność.

Zauważmy, że w powyższej analizie nie użyłem w ogóle NSP. Mogłoby się więc wydawać, że mówimy o każdej stopie procentowej. A jednak nie. Chodzi tu tylko o NSP. Dlaczego? W tym schemacie od początku zakładamy, że kredyt w całości pokrywa produkcję i stąd odsetki są rzeczywiście jedynym faktycznym kosztem. Poniższy przykład pozwoli dogłębnie zrozumieć gdzie leży pies pogrzebany.

Powiedzmy, że są dwie firmy: pierwsza to zwykły przedsiębiorca, a druga to "bank". Pierwsza pożycza od "banku" maszynę, za pomocą której produkuje olej i w zamian oddaje trochę tego oleju w ramach odsetek. Zgodnie z warunkiem maksymalizacji zysków dodatkowa produkcja (sprzedana) będzie równa kosztowi, czyli odsetkom na jednostkę produkcji. Widzimy, że dostaliśmy jakby masło maślane, bo dodatkowa ilość oleju ma być równa ilości oleju. Wydawać by się mogło, że kosztem powinniśmy ustanowić samo używanie wypożyczonej maszyny do produkcji oleju. Jednakże firma nie jest właścicielem tej maszyny, a tylko ją pożyczyła. A to znaczy, że jej nie amortyzuje, a przecież amortyzacja wyraża właśnie zużycie maszyny. A zatem zostają tylko odsetki. Firma płaci za maszynę właśnie swoim wytworem - to olej jest ekwiwalentem pieniądza. Stąd wynika, że jeśli rynkowa stopa procentowa jest równa NSP, to warunek maksymalizujący zysk będzie spełniony - krańcowa produktywność (NSP) zrównuje się z krańcowym kosztem (stopa procentowa).

Powiedzmy jednak, że NSP wzrasta. To oznacza, że firma zwiększyła produktywność. To znaczy, że krańcowy przychód wzrośnie, ale odsetki się nie zmieniły - firma płaci ciągle tyle samo oleju! Firma może więc zwiększyć zysk, skoro warunek maksymalizacji nie jest spełniony. Pytanie jak? Najłatwiej będzie, jeśli wprowadzimy trzecią firmę, która np. sprzedaje produkty mleczne. Pierwsza firma może wyprodukować więcej oleju niż dotychczas i wymienić go za mleko w transakcji z trzecią firmą. Mleko staje się nowym rodzajem przychodu. Teraz olejarnia musi żądać od mleczarni takiej ilości mleka za jedną butelkę oleju, aby przychód krańcowy (mleko) zrównał się w końcu z kosztem krańcowym (olej).  Co ważne, wymiana z bankiem nie zmieniła się, po prostu zwiększyła produkcję i zysk. 

Powyższy schemat dowodzi, że NSP to krańcowa produktywność. Gdy rynkowa stopa leży poniżej NSP, to odsetki pozostają całkowitym kosztem krańcowym, ale przestają równać się krańcowemu przychodowi, stąd rynkowa stopa przestaje stanowić krańcową produktywność.

W art.  Zerowa stopa procentowa to zerowe inwestycje? pokazałem, że stopa procentowa stanowi stopę wzrostu z inwestycji całej gospodarki. W rzeczywistości wyprowadzenie tego twierdzenia opierało się na założeniu, że wydatki równają się dochodom. Ma to swoje uzasadnienie w zasadzie memoriałowej oraz współmierności kosztów i przychodów w księgowości, niemniej ilość pieniędzy krążących w gospodarce nie musi się pokrywać z wartością sprzedanych dóbr i usług. Innymi słowy wydatki nie muszą być równe dochodom. Ale właśnie tamto wyprowadzenie idealnie odpowiada NSP i to do niego się odnosi: warunkiem jest, aby inwestycje zinterpretować nie jako część całego kapitału, ale jak jego zmianę. Taki warunek będzie spełniony, jeśli w każdym okresie otrzymujemy pewien zysk, który właśnie można traktować jak zmianę posiadanego kapitału. Wtedy część tego zysku przeznaczona będzie na inwestycje, a więc ta część będzie po prostu "dochodem inwestycyjnym". I dopiero z tego dochodu inwestycyjnego przedsiębiorca-inwestor generuje jego wzrost. Tak powstanie NSP i w równowadze stopa procentowa będzie jej równa. 

Dam teraz głos Wicksellowi, który przedstawia podobne rozumowanie:

Załóżmy teraz, że banki i inni pożyczkodawcy pieniędzy udzielają pożyczek według innej stopy procentowej, niższej lub wyższej, niż ta, która odpowiada aktualnej wartości naturalnej stopy procentowej kapitału. Równowaga ekonomiczna systemu zostaje ipso facto zakłócona. Jeśli ceny pozostaną niezmienione, przedsiębiorcy w pierwszej kolejności uzyskają nadwyżkę zysku (kosztem kapitalistów) ponad ich rzeczywisty zysk przedsiębiorcy lub płacę. Będzie on narastał tak długo, jak długo stopa procentowa pozostanie w tej samej pozycji względnej. Nieuchronnie będą oni zachęcani do rozszerzania swojej działalności, aby maksymalnie wykorzystać korzystną sytuację. A liczba osób stających się przedsiębiorcami będzie nienaturalnie zwiększona. W konsekwencji zwiększy się popyt na usługi, surowce i towary w ogóle, a ceny towarów muszą wzrosnąć.

Jeśli stopa procentowa wzrasta, powstaje sytuacja odwrotna. Tak długo, jak ceny pozostają niezmienione, przedsiębiorcy cierpią na niedostatek poniżej swoich normalnych dochodów. i pojawia się tendencja do ograniczania działalności gospodarczej do jej bardziej zyskownych elementów. Popyt na towary i usługi spada, a w każdym razie nie nadąża za podażą; a ceny spadają.

(str. 105-106)

Zanim przejdę do dalszego fragmentu zwrócę uwagę, że tutaj Wicksell analizuje problem po zmianie rynkowej stopy procentowej. Natomiast w poniższym odwrotnie - to NSP się zmienia. Pozornie wydaje się, że na to samo wychodzi, ale jednak wzrost NSP oznacza, że rośnie produktywność całej gospodarki, co może oznaczać zarówno wzrost z tytułu postępu technicznego jak i po prostu ożywienie gospodarcze. Gospodarka nic na tym nie traci, tylko zyskuje. Natomiast gdy stopa bankowa spada, to produktywność się nie zmienia; jest to trudniejsza sytuacja do analizy. Wicksell wydaje się nie zauważać tej różnicy. Przejdźmy teraz do rozdziału 9 (dalszy wywód rozdziału 8-go okazuje się niejasny, mało klarowny i rozwlekły).

Należy teraz przypuszczać, że z jakiegoś powodu powstaje różnica między naturalną stopą procentową a umowną stopą procentową. Może to być spowodowane, na przykład, spadkiem poziomu płac (spowodowanym względnym wzrostem liczby pracowników), spadkiem renty gruntowej lub innych rent, czy wreszcie wzrostem wydajności pracy i sił przyrody w wyniku postępu technicznego. Załóżmy, że stopa naturalna zostanie podniesiona do i +1 procent, podczas gdy banki utrzymają swoją zwyczajową stopę dyskontową i.

Dla kogo ta różnica będzie korzystna? W pierwszej kolejności, oczywiście, przedsiębiorcom. Pod koniec roku ich produkt, wyceniony na normalnym poziomie cen, wyniesie K(1 + (i+1)/100), podczas gdy kwota, którą są winni, to tylko K(1 + i/100) . W ten sposób uzyskali nadwyżkę zysku w wysokości K/100 i mogą ją zrealizować, wymieniając między sobą odpowiednią ilość towarów i przeznaczając je na konsumpcję w nadchodzącym roku; natomiast resztę swoich zapasów oferują kapitalistom po cenach normalnych, to znaczy za całkowitą sumę pieniędzy K(1 + i/100). W pierwszej kolejności, poziom cen pozostaje niezmieniony.

(...)

Jeśli przedsiębiorcy nadal, być może rok po roku, będą osiągać nadwyżki zysku tego rodzaju, to rezultatem może być jedynie powstanie tendencji do rozszerzenia ich działalności. Podkreślam raz jeszcze, że jak dotąd jest to wyłącznie kwestia tendencji. Rzeczywiste rozszerzenie produkcji jest niemożliwe, ponieważ wymagałoby zwiększenia podaży realnych czynników produkcji, pracy i ziemi, lub zwiększenie ilości realnego kapitału stałego i płynnego kapitału, tak aby dostępne pierwotne czynniki produkcji mogły być wykorzystane w dłuższym, a więc bardziej produktywnym procesie. Zmiany takie wymagają czasu, aby mogły być dokonane, i nie musimy ich w tym momencie rozważać. Załóżmy, że wszystko pozostaje po staremu, lub że co najwyżej, w wyniku np. wydłużenia godzin pracy, następuje pewien nie kumulatywny wzrost produkcji, którego wpływ na ceny nie jest progresywny i dlatego zostanie zaniedbany.

(...)

Tendencja do zwiększania produkcji jednak działa i powoduje wzrost popytu na pracę i inne czynniki produkcji - a w aktualnych warunkach także na surowce, półprodukty i tym podobne. Płaca pieniężna i czynsze pieniężne idą w górę i chociaż nie następuje ogólny wzrost produkcji, przedsiębiorcy są zmuszeni pożyczać od banków więcej kapitału na produkcję bieżącego roku. Nie da się bezpośrednio określić, o ile wzrosną płace, a więc o ile trzeba będzie zwiększyć kapitał przemysłowy. Ale przy naszym założeniu można ustalić pewną granicę. Jeśli przedsiębiorcy nie liczą się na razie z jakimkolwiek wzrostem cen w przyszłości, to górną granicą możliwego wzrostu płac jest spadek stopy procentowej. Dla uproszczenia przyjmiemy, że ta górna granica zostaje natychmiast osiągnięta i że kapitał żądany od banków wynosi teraz 1,01 K. 

Ten wzrost popytu na kredyty może być zaspokojony przez banki równie łatwo, jak poprzedni czy jakikolwiek inny popyt. Nie wymaga to podwyższenia stopy procentowej i przyjmiemy, że zostanie ona utrzymana na poziomie i procent. Niemniej jednak można by sądzić, że wzrost płac musi pozbawić przedsiębiorców całej nadwyżki zysku, na którą liczą w bieżącym roku. Ale co się właściwie dzieje? Jeśli robotnicy i właściciele ziemscy zwiększą swoje zapotrzebowanie na towary do konsumpcji w roku bieżącym do tego stopnia, że wzrosły płace pieniężne i czynsze pieniężne, to ten zwiększony popyt zostanie zaspokojony przez taką samą ilość kapitału towarowego jak poprzednio. Z konieczności prowadzi to do wzrostu wszystkich cen - wzrostu, który najprościej jest uznać za proporcjonalny do wzrostu popytu. Wynika z tego, że kwota płacona za cały kapitał towarowy, którego wartość wynosiła poprzednio K, wynosi teraz 1,01 K.

(str. 141-144)

Tak jak wyżej stwierdziłem należy odróżnić sytuacje, gdy NSP rośnie ponad i oraz gdy i spada poniżej NSP. Przeanalizujmy więc teraz obie sytuacje po kolei.

A) NSP rośnie ponad stopę i, a i pozostaje stała

Etap 1: wzrost podaży

Gdy NSP rośnie, to jest tak samo, jakby nastąpił przyspieszony postęp techniczny. Krótkoterminowa lub długoterminowa krzywa podaży przesuwa się w prawo:

Etap 2: wzrost popytu

Wzrost podaży przekłada się automatycznie na wzrost popytu. Wzrasta bowiem popyt na pieniądz (na nowe inwestycje i konsumpcję) i podaż pieniądza (kredyty), co przesuwa krzywą popytu w prawo:

W konsekwencji nastąpił wzrost PKB, a cena się nie zmieniła. Wniosek: Wicksell się myli. Oczywiście można rozbijać problem na czynniki pierwsze i dochodzić do keynesowskich mnożników i akceleracji, ale to szczegóły, rzeczy wtórne, bo te efekty mogą występować po dowolnym wstrząsie i nie muszą przynosić trwałych zmian cenowych.

B) Rynkowa stopa i spada poniżej NSP, a NSP pozostaje stała

Ponieważ jest to znacznie bardziej skomplikowana sytuacja rozpiszemy problem krok po kroku na poprzednim przykładzie olejarnia vs. bank. Zakładamy tym razem, że NSP nie zmienia się, ale bank obniża i. To motywuje olejarnię do zwiększenia produkcji. Ale ponieważ sama produktywność nie wzrosła, to cały mechanizm zaczyna się od zwiększenia popytu na surowce i pracę poprzez zwiększenie kredytu. 

Etap 1. W krótkim terminie rośnie popyt, a podaż stoi (nie następuje wzrost produktu). Z tego powodu cena wzrasta z p1 do p2:

Już w tym miejscu można się pogubić. Dlaczego? Skoro produkcja nie wzrosła, a jednocześnie działamy w gospodarce barterowej, to co to znaczy, że cena wzrosła? Jeśli firma nie ma towaru, którym zapłaci za czynniki wytwórcze, to musi oddać maszynę (lub jej część), którą pożyczyła od "banku". Konkretniej, powiedzmy, że olejarnia zatrudnia osobę do pracy przy maszynie, a wynagrodzeniem będą akcje tej maszyny. Na rynku pracownik wymienia je na odpowiednie towary do własnej konsumpcji. W krótkim okresie towarów nie przybywa za dużo, wobec tego żeby je dostać, musi sprzedać więcej akcji. Siła nabywcza maszyny staje się miarą ceny, a więc spadek tej siły staje się miarą inflacji. 

Etap 2. Ponieważ popyt na kredyty wzrósł, to podaż kredytów powinna też wzrosnąć. Trzeba się teraz zastanowić czy rzeczywiście bank może zaspokoić popyt na pieniądz. Z jednej strony wiemy, że to jest moment różnicy między gospodarką barterową a monetarną - bank nie może wytworzyć maszyn służących do leasingu w ciągu krótkiego okresu, którym operujemy (pamiętajmy, że jego produktywność, tak jak całej gospodarki, nie rośnie w tym schemacie), a pieniądz może (jako zapis księgowy). Z drugiej strony "produkcja" pieniądza to nie wszystko, bo należy też doliczyć obsługę kredytu. A przyjęliśmy przecież, że w krótkim okresie firmy nie zwiększają produkcji. Bank stanowi część tego systemu, a więc w uśrednieniu także podlega tej zasadzie.

Banki jednak wyróżniają się w tym systemie i jako ułamek wszystkich przedsiębiorstw, moglibyśmy je uprzywilejować w ten sposób, że posiadają pewne rezerwy. Uzasadnienie tego założenia byłoby następujące. Przy większej stopie i bank musi mieć pewne rezerwy na wypadek niespłacenia kredytów przez klienta. Mniejsze i zmniejsza ryzyko, że klient nie spłaci kredytu, a więc można rezerwy przeznaczyć obsługę kredytów, ewentualnie na dodatkową podaż. W sumie koszty jednostkowe (prawie) nie rosną, a podaż pieniądza rośnie. Dlatego bank będzie w stanie zaspokoić popyt na pieniądz do poziomu wyznaczonego przez własne rezerwy. 

Jedna uwaga. Wg Wicksella inflacja będzie się utrzymywać, tak długo aż bank nie zwiększy i. Ceny mają coraz silniej rosnąć, ponieważ firmy mogą bez przerwy wykorzystywać nadwyżkę NSP nad i poprzez ciągłe zwiększanie kredytu, tak by zredukować koszty inflacyjne. W ten sposób ma wystąpić samonakręcająca się spirala płacowo-cenowa. Z tą tezą nie mogę się zgodzić przede wszystkim z tego powodu, iż rezerwy, o których wyżej pisałem, są ograniczone. Wicksell zakłada, że bank może bez żadnych ograniczeń np. zaciągać dług w banku centralnym i stąd mieć pieniądze na kredyty i rezerwy. Oczywiście jest to możliwe, jednak prędzej czy później ograniczyłaby go jego własna produktywność.  Żeby temu zapobiec, musiałby bez przerwy zwiększać swoją wydajność. Ale to po prostu prowadzi do postępu technicznego, który w modelu ograniczony jest przez NSP.

Etap 3. Skoro bank zmniejszył i, to znaczy, że zarabia mniejsze odsetki na każdym kredycie. Ale z etapu 2 wiemy, że mniejsze odsetki kompensuje sobie większą wartością kredytów. Powstaje pytanie czy kompensuje w pełni czy częściowo? Odpowiedź nie jest prosta, dlatego podejdziemy do tego zadania od strony maksymalizacji zysków. Załóżmy, że przed obniżką i bank maksymalizował zyski. Czyli jego koszt krańcowy był równy przychodowi krańcowemu. Stwierdziliśmy wyżej, że koszty nie rosną wraz ze spadkiem i, a zatem koszt krańcowy nie zmienia się. Gdyby więc przychód krańcowy też się nie zmienił, to bank nadal maksymalizowałby zyski i byłaby szansa, że ogólny zysk nie spadnie. 

Przeanalizujmy w takim razie przychód krańcowy banku. Wiadomo, że cały przychód wynosi i*K. Wiemy też, że im mniejsze i, tym większy popyt na kredyt K. Na rysunkach operowaliśmy liniowymi funkcjami, więc zachowamy to uproszczenie, przyjmując i = a - b*K , gdzie a oraz b to liczby dodatnie. W takim razie przychód wynosi (a - b*K)*K = a*K - b*K^2. Krańcowy przychód to pochodna po K, a więc wynosi a - 2*b*K. Stąd im większe K, tym mniejszy przychód krańcowy. A zatem skoro koszt krańcowy nie zmienia się, a przychód krańcowy spada, to znaczy, że bank nie maksymalizuje zysków. 

Nie oznacza to jeszcze, że bankowi spadły zyski, tylko że nie są maksymalne. Powiedzmy, że i spada o 1 pkt proc. Aby bank wyrównał przychody, to K musiałby wzrosnąć o pewien x:

 

Ale to są tylko przychody. Aby zysk nie spadł musi zostać zachowana równowaga:
 

 

 

Rozwiązanie względem x to:

 

 

Gdyby stopa spadła z 4 na 3, kredyt musiałby wzrosnąć o 1/3 (tj. x = 0,33). Spadek stopy z 2 na 1%, wymagałby wzrostu kredytu o 100%. W lepszej sytuacji bank znalazłby się, gdyby początkowa stopa była większa. Np. przy spadku z 10 na 9%, x = 1/9, co uprawdopodobniałoby zachowanie zysku.

 

Jeżeli okres kredytowania trwa dłużej niż rok, to sytuacja już się komplikuje. Aby kredyt pozostał zrównoważony, równanie przychodów musi być postaci:

 

 

gdzie N to okres kredytowania.

 

Aby zysk nie spadł musi zostać zachowana równowaga:

 

 Przyjmijmy za i = 4% i N = 3. Wtedy spadek stopy z 4 na 3% sprawiłby, że kredyt musiałby już wzrosnąć o 35% (tzn. rozwiązanie wynosi x = 34,66%). Gdy okres N wzrasta do 10, x = 40%. A więc im dłuższy okres trwania kredytu, tym skompensowanie strat byłoby coraz trudniejsze.

 

W sumie więc bank mógłby się zgodzić na niższe oprocentowanie, gdyby miał zapewnioną odpowiednio dużą wielkość kredytów. Trzeba pamiętać, że ta strategia jedynie minimalizuje utratę maksymalnych zysków.

Etap 4. Bank orientuje się, że przestał maksymalizować zyski (i być może w ogóle je tracić). Jeżeli z jakiegoś powodu nie może podnieść stopy i, to zacznie zmieniać się w inwestora zarabiającego na dywidendach lub na obligacjach korporacyjnych. Ponieważ NSP > i, to znaczy, że stopa zwrotu z innych walorów będzie wyższa niż i nawet po skorygowaniu o dodatkowe ryzyko. Wzrost popytu na te walory spowoduje wzrost ich ceny, a co za tym idzie spadek stopy zwrotu. W sumie stopa zwrotu z akcji / obligacji zrówna się z NSP. Oczywiście jeśli banki mogą podnieść od razu i do NSP to to zrobią i nie będzie potrzebne kupowanie akcji. 

Etap 5. Ponieważ bank zarabia na dywidendach i obligacjach albo też zwiększa stopy, to zmniejsza podaż pieniądza, co zmusza popyt na pieniądz do spadku, co przesuwa krzywą popytu na rynku towarowym w lewo - popyt wraca do punktu wyjścia: 

Można w uproszczeniu powiedzieć, że na początku ludzie zwiększają popyt na pieniądz i popyt na towary rośnie (etap 1), co wywołuje inflację, a na koniec mają mniej pieniędzy, więc popyt na towary spada (etap5). Cena powraca do punktu wyjścia. 

Wspomniałem o spadku podaży pieniądza. Ona spadnie tylko dlatego, że musi się dostosować do spadkowego popytu na pieniądz, który będzie spowodowany powrotem stopy procentowej do wyższego poziomu albo ograniczeniem akcji kredytowej przez same banki (które przenoszą inwestycje na rynek akcji). Ale de facto w krótkim okresie ludzie ciągle będą spłacać kredyty, czyli bardziej prawdopodobne będzie utrzymanie się stanu inflacji. Dopiero spłata "nadmiernego" długu doprowadzi do ustabilizowania się cen, a to stanie się w długim okresie. Jednocześnie krzywa podaży stanie się nachylona (obraca się wokół bieżącej ceny):

Gdyby z jakiegoś powodu podaż pieniądza nie wróciła do pierwotnego poziomu, np. ludzie zaciągnęliby kredyty na 30 lat na stałą stopę %, która była niższa od NSP, wtedy rzecz jasna powrót ceny byłby bardzo powolny.

Nie przeprowadzam już analizy w drugą stronę, tj. gdy NSP < i, ponieważ będzie to analogia, ale tym razem to przedsiębiorstwa będą rezygnować z kredytów, których oprocentowanie będzie za wysokie. A będzie za wysokie, bo przekroczy ich produktywność krańcową, co spowoduje, że ich zyski nie osiągną max. Zaczną szukać kapitału gdzie indziej, np. wśród innych przedsiębiorstw. Te z kolei mogą być chętne do udzielania pożyczek, jeżeli oferowana stopa procentowa będzie odpowiednio wyższa od oprocentowania lokat. Kapitał zacznie więc odpływać z banków, co sprowokuje je do obniżenia i, do takiego poziomu, aby przywrócić popyt na kredyt.

Uzasadnione pytanie

Dlaczego w schemacie (A) banki na koniec nie stają się również inwestorami akcyjnymi tak jak w schemacie (B)? Różnica jest taka, że w schemacie (B) siła zewnętrzna obniża stopę proc. i, która jest obserwowalna, a więc banki wiedzą, że NSP jest wyższa. Natomiast w schemacie (A) NSP sama wzrasta, a przecież jest to wielkość nieobserwowalna i banki mogą nie wiedzieć, że wzrosła.

Podsumowanie

Wicksell stworzył bardzo interesującą koncepcję naturalnej stopy procentowej, którą banki centralne powinny starać się naśladować ustalając stopy redyskontowe. Jeżeli Wicksell ma rację, to, gdy rynkowa stopa % jest mniejsza od NSP, ceny w gospodarce powinny rosnąć, a gdy większa - spadać. W tym artykule starałem się teoretycznie wykazać, że jego teza sprawdzi się pod tym względem gdy są spełnione dwa warunki:

- NSP nie zmienia się, a stopa % rośnie lub spada oraz gdy

- banki zachowują się nieracjonalnie i nie adaptują się szybko do NSP. Jeżeli i < NSP, to powinny przynajmniej wejść na rynek dłużny otrzymując NSP. Jeżeli jednak kierunek stopy % wyznacza bank centralny, to nie powinny obniżać swojej RRSO. Można by tutaj zastanowić się nad bankami państwowymi, które świadomie ograniczałyby zyski do budżetu państwa, realizując określone cele gospodarcze; w dłuższej perspektywie jest to ryzykowne - polityka niskich stóp procentowych była jedną  z przyczyn kryzysu finansowego 2007-2009.

 

* Fragmenty przetłumaczyłem z pomocą www.DeepL.com z małymi poprawkami ręcznymi.

Literatura:

Knut Wicksell, Interest and Prices, 1898 , Originally published, 1936. Reprinted 1962 by arrangement with the Royal Economic Society.

Naturalna stopa procentowa - wstęp

Czy istnieje coś takiego jak stopa procentowa w stanie równowagi? Albo inaczej, czy można określić prawidłową stopę (np. referencyjną, redyskontową), jaką powinien przyjąć bank centralny? Chociaż nie ma jednolitego stanowiska w tym temacie, to wszyscy się zgodzą, że optymalna stopa procentowa powinna stabilizować co najmniej 2 zmienne: inflację i zmiany PKB. Jeśli chodzi o inflację, to wg mnie powinna wynieść 0, a jeśli już ma być dodatnia, to nie więcej niż 1,5% (opisałem to w art. Optymalna inflacja? ). Jeżeli chodzi o PKB, to sprawa jest prostsza: optymalnie powinno zmieniać się tak samo jak potencjalny PKB (tj. PKB przy minimalnym poziomie bezrobocia), czyli luka PKB powinna wynieść 0%. Wgłębiając się w temat okazuje się, że sprawa jest bardziej skomplikowana, bo inflacja zależy od luki PKB (zob. Inflacja a luka PKB). Rzecz w tym, że na inflację wpływa kilka czynników i luka PKB jest jednym z nich. Drugim czynnikiem byłaby właśnie stopa procentowa (r). 

Wpływ stopy procentowej na popyt, podaż i cenę

Jeżeli r staje się za niska, wówczas jednostki (w tym państwo) starają się to wykorzystać, sięgając po tani kredyt, maksymalizując konsumpcję czy inwestycje. Tyle że popyt dużo szybciej dostosowuje się do warunków rynku niż podaż. Popyt może wzrosnąć natychmiast, podczas gdy podaż jest ograniczona zdolnościami wytwórczymi (które można zwiększyć za pomocą inwestycji, ale dzieje się to w długim czasie) oraz kontraktami. W związku z tym, aby doszło do równowagi rynkowej, cena musi wzrosnąć. Pokażmy to na wykresie:

Rysunek 1- krótki okres

Y - ilość produktu lub usług,
P - cena produktu lub usług.

W krótkim okresie linia opadająca reprezentuje popyt, pionowa - podaż. W p. A jest początkowa równowaga. W tym punkcie PKB = potencjalny PKB. Należy zaznaczyć, że PKB to nie jest ani popyt, ani podaż, ale punkt równowagi popytu i podaży. Pamiętać trzeba również, że mówimy tu o realnym PKB, a nie nominalnym. Są to dwie różne wielkości, których nierozróżnianie prowadzi do wielu nieporozumień i błędów myślowych. Czyli żeby nie było wątpliwości - PKB to ilość dóbr i usług oferowanych przez firmy i pożądanych przez konsumentów.

W podstawowym modelu popytu i podaży nie znajdziemy oczywiście zmiennej w postaci stopy procentowej. To znaczy, że r stanowi czynnik zewnętrzny i jej zmiana spowoduje, że linia popytu zacznie się przesuwać w prawo lub lewo. Gdy r spada, następuje przesunięcie w prawo, wzrost popytu z y1 do y2, ale cena p1 pozostaje jeszcze stabilna - otrzymujemy p. B. Ale ponieważ popyt przewyższa podaż, przedsiębiorcy zaczną zwiększać cenę swoich produktów, ponieważ nie mogą zaspokoić popytu. W związku z tym cena podnosi się do p2, a popyt wraca do poziomu y1 - otrzymujemy nowy poziom równowagi rynkowej - p. C. 

W tym modelu warto uwzględnić rynek pieniężny, który ma wpływ na rynek towarowy. Spadek ceny pieniądza, tj. stopy %, oznacza, że popyt na pieniądz rośnie. Aby zachować równowagę, podaż pieniądza też musi wzrosnąć. Ponieważ banki komercyjne nie mogą wyczarować pieniędzy, a tzw. kreacja pieniądza to tylko nazwa i opiera się na dwóch czynnikach: popycie na pieniądz oraz szybkości obiegu pieniądza (czym jest kreacja pieniądza wyjaśniłem w tym artykule), to pożycza je w transakcji repo od banku centralnego (który rzeczywiście je wyczarowuje) i udziela ludziom kredytów. Czyli bank centralny zwiększa podaż pieniądza, tak aby zaspokoić rosnący popyt na pieniądz. Przykładowo firma dostaje na rozwój, ale już wiemy, że zajmuje to trochę czasu, co przekłada się na krótkookresową inflację. Lecz samonapędzająca się gospodarka sprawia, że ten mechanizm to dopiero początek. Firma wydaje kredyt na nowy sprzęt, zatrudnienie itd., a zatem ktoś inny na tym zarabia. Ponieważ r jest niska, to zarabiający ponownie nie będzie lokował dochodu w banku, a wydawał. Rośnie konsumpcja i inwestycje, których znów podaż nie może zaspokoić. Muszą więc znów podnieść ceny. Kolejne firmy chcąc nadążyć za popytem, zaciągają kredyty na te inwestycje. Banki muszą ponownie zwiększyć ilość pieniędzy w gospodarce. Firmy znów wydają, ktoś znów zarabia i znów ze względu na słabe zyski z lokat zwiększa konsumpcję... Inflacja znowu wzrasta.

To znaczy, że wzrost podaży pieniądza to kolejny czynnik przesuwający krzywą popytu na towary w prawo:

 Rysunek 2 - krótki lub średni termin

  

Podsumowując, obniżenie stopy procentowej powoduje jakby podwójny wzrost cen: najpierw bezpośrednio przez niedostosowaną podaż dóbr i usług, a następnie przez wzrost podaży pieniądza, która dodatkowo generuje popyt i tym samym zwiększa lukę między popytem a podażą. Aby ją zlikwidować, należy podnieść ceny.

Czy dałoby się ograniczyć szkody inflacyjne do samej obniżki r bez zwiększania podaży pieniądza? Może należałoby po prostu zrezygnować z tego dodatkowego worka pieniędzy? Nie ma takiej możliwości. Bank skądś musi wziąć je na nowe kredyty. Zauważmy, że gdyby było odwrotnie, tzn. podniesiono by r, to bank więcej by zarobił i te nadwyżki mogłyby posłużyć jako dodatkowy kredyt (w tym dłuższym terminie).

Czy to znaczy, że sterowanie stopą procentową przynosi same szkody? 

Nie, bo jeżeli od początku r była za wysoka, to obniżenie będzie jedynie przywróceniem jej równowagi. I na odwrót, jeżeli była za niska, to jej zwiększenie pozwoli ograniczyć inflację. Cała sztuka polega na określeniu stopy w równowadze.

Z powodu kryzysu finansowego 2007-2010 realny PKB USA znalazł się poniżej potencjalnego. Dlatego rząd USA, stosując bardzo rozbudowany interwencjonizm, m.in. poprzez zerowe stopy (jeszcze w 2007 r. stopa rezerw federalnych wynosiła ponad 5%, a w 2009 r. prawie 0) i bailouty, nie wywołał dużej inflacji. Jest to dobry rodzaj keynesizmu, który przez wielu pozostaje niezrozumiany i krytykowany. Z drugiej strony nie-ekonomiści, np. politycy czy dziennikarze, wykorzystują keynesizm w celu propagowania wszelkiego interwencjonizmu, co prowadzi do wypaczenia idei Keynesa. Przykładem złego interwencjonizmu jest polityka NBP zarządzanego przez obecne władze. Nie będę już powtarzał argumentów, a jedynie odeślę do artykułu Inflacja a luka PKB , gdzie to omówiłem.

Kalibracja stopami może być korzystna także jako swego rodzaju placebo - efekt ekonomiczny może zostać uzyskany pośrednio przez psychologiczny. Polityka stałych stóp zmniejsza niepewność co do przyszłości.

Jeżeli nie nastąpi kolejny bodziec pieniężny, to efekt inflacyjny (nawet spirala cenowo-płacowa) zacznie wygasać. W długim okresie przedsiębiorcy zwiększą moce przerobowe i podaż wzrasta do y3, któremu odpowiada cena p3. Podaż staje się linią nachyloną rosnącą. Otrzymujemy nowy poziom równowagi rynkowej - p. D:

Rysunek 3 - długi okres

Chociaż podaż się dostosowała, to cena p3 jest wyższa niż pierwotna p1. To oznacza, że koszt czynników wytwórczych wzrósł. Czynniki wytwórcze to np. zatrudnienie albo materiały. Skoro wynagrodzenie pracowników wzrosło, to znaczy, że trudniej o pracownika. A skoro trudniej o niego, to znaczy, że bezrobocie jest niższe. Jeżeli bezrobocie spadnie poniżej poziomu bezrobocia naturalnego (4-6%), to PKB będzie powyżej potencjalnego PKB (będzie to y2). Aby zapobiec tej sytuacji, musiałby nastąpić postęp techniczny, który umożliwiłby zmniejszenie zatrudnienia w jednostce czasu (bezrobocie wraca do naturalnego). Jednocześnie na skutek spadku zatrudnienia popyt nieco spadnie.  Trzeba pamiętać, że początkowy wzrost popytu powstał sztucznie poprzez pożyczki oraz podaż pieniądza. Postęp techniczny działa na przekór podaży pieniądza - pozwala mniej płacić. Pożyczki można teraz szybciej zwrócić, a więc wszystko się dzieje na odwrót z punktu widzenia popytu i stąd jego spadek. Odzwierciedleniem tej sytuacji jest przesunięcie linii podaży w prawo oraz lekkie cofnięcie popytu w lewo:

Rysunek 4 - hipotetyczny postęp techniczny (długi okres)

 

Ostateczny punkt ustaliłby się w p. E. Zauważmy, że został zachowany poziom y3 z długiego okresu, a cena powróciła z p3 do pierwotnej p1. Jeżeli y1 stanowił początkowo potencjalny PKB, to wzrost do y3 bez zmiany ceny musi oznaczać nowy potencjalny PKB. Postęp techniczny zwiększył potencjalny PKB z y1 do y3 bez inflacji. To najlepszy układ dla gospodarki, ale najtrudniejszy do osiągnięcia.

To tylko wstęp

W zasadzie nawet nie poruszyłem koncepcji naturalnej stopy procentowej (NSP) mimo pewnego wprowadzenia. Dlaczego w powyższej analizie nie wspomniałem nawet o niej? Zauważmy, że Rysunek 1 wskazuje, że spadek r prowadzi do wzrostu ceny nie zmieniając w sumie poziomu PKB. PKB powrócił do poziomu potencjalnego. Ale zgodnie z koncepcją NSP również r powinna powrócić do pierwotnego poziomu równego NSP. Czyli NSP to r, dla której PKB = potencjalny PKB. Tymczasem w opisanym dotychczas modelu r pozostaje zawsze na tym zmniejszonym poziomie, a ceną tego zmniejszenia jest inflacja. Widzimy więc, że żeby się nie pogubić w temacie, należy go uporządkować. W następnej części przeanalizuję te różnice.