Zmagania z modelem log-periodycznym

Do teorii log-periodycznej od dawna byłem sceptycznie nastawiony, a swoją krytykę wyraziłem kiedyś w tym artykule. Z drugiej strony jestem zwolennikiem teorii chaosu (choć może nie deterministycznego), a więc także nieokresowych i nietrywialnych cykli. Ekonofizyka dostarcza także uzasadnienie powstania tzw. log-periodyczności. Nie jest wykluczone, że dla niektórych okresów lub niektórych walorów, teoria ta może się sprawdzić i tym samym wspomóc inwestora czy spekulanta w podjęciu trudnych decyzji. Co więcej, Sornette i Johansen [1] rozważają najpierw w swoim modelu "ograniczoną racjonalność" traderów (która wynika nie tylko z ułomności ludzkiego umysłu, ale także z natłoku informacji), a następnie [2, 3, 4] tworzą model w ramach racjonalnych oczekiwań, zgodnie z którym moment krachu można prognozować, ale tylko z pewnym prawdopodobieństwem. Ogólnie autorzy twierdzą, że gracze sami "się nakręcają" i kreują dodatnią warunkową oczekiwaną stopę zwrotu, która staje się tym wyższa im bliżej jest krachu. Ale staje się ona wyższa nie dlatego, że gracze "nakręcają się" w sposób nieracjonalny, ale dlatego, że gracze wymagają od rynku wyższej oczekiwanej stopy zwrotu właśnie za to, że się nakręcają. A nakręcają się w sposób racjonalny, dlatego że zdają sobie sprawę, że - w przypadku trendu rosnącego - kupując w takiej fazie, więcej ryzykują. Im bliżej krachu, tym więcej ryzykują, a więc wymagają większego zwrotu. Rozdzielając oczekiwaną stopę zwrotu na prawdopodobieństwo i wielkość ruchu, można powiedzieć, że prawdopodobieństwo dalszego (czyli warunkowego) wzrostu spada, natomiast zakres ruchu rośnie. Natomiast niewarunkowa stopa zwrotu pozostaje równa zero. Aby dobrze zrozumieć różnicę między warunkową a niewarunkową stopą zwrotu, dobrze najpierw przeczytać wpis Smarujący estymator.

Autorzy podkreślają, że nie wystarczy tylko raz zastosować model, który wyprognozuje moment krytyczny i czekać do tego okresu. Jeżeli model wskazuje moment krytyczny za rok, to w ciągu tego roku może się struktura zmienić, więc należy aktualizować model. To jest dodatkowy stochastyczny element ich teorii.

Jest wiele różnych wersji modelu log-periodycznego, ale właściwie wszędzie pojawia się wzór, który w uproszczeniu wyprowadzę idąc tokiem rozumowania Kutnera [5]. Ogólnie biorąc musimy połączyć dwie koncepcje: jedną ze statystyki - rozkład Levy'ego-Pareto i jedną z fizyki - temperatury krytycznej. Podzielę to na dwie części.

1) Rozkład Pareto-Levy'ego jest związany z grubymi ogonami, które dobrze są nam znane, więc nie będę się o nim rozpisywał. Jeśli cenę akcji P(t) da się opisać rozkładem proporcjonalnym do:

(1)

to mamy do czynienia z rozkładem Pareto dla t > 0. Zwróćmy uwagę, że z jednej strony wzór (1) opisuje prawdopodobieństwo (zmiany) ceny, ale z drugiej wartość oczekiwana będzie proporcjonalna do tego prawdopodobieństwa. Zgodnie ze wzorem (1) dla każdego okresu t mamy inne prawdopodobieństwo. Gdybyśmy przemnożyli obie strony przez cenę P(t), to dostalibyśmy wartość oczekiwaną ceny dla okresu t. Stąd w miejsce prawdopodobieństwa możemy wstawić po prostu oczekiwaną cenę.

Znaną własnością rozkładu Pareta jest równanie skalowania:

(2)

gdzie L^a to czynnik skalujący funkcję P(t).

Najogólniejszym rozwiązaniem osobliwym (tzn. rozwiązaniem, które nie posiada zapisu zgodnego z całką ogólną - gdyż mamy tu do czynienia z równaniem różniczkowym zwyczajnym) równania skalowania (2) jest

(3)

Funkcję F(u) można rozwinąć w szereg Fouriera:

(4)

2) W złożonych systemach istnieją różne fazy, w których pewne parametry fizyczne / ekonomiczne pozostają względnie stałe. W fizyce takimi parametrami są temperatura lub ciśnienie. Np. faza topnienia następuje w temperaturze poniżej 0 stopni Celsjusza, faza zamarzania - od 0 stopni wzwyż, a faza wrzenia - 100 stopni. Hołyst, Poniewierski i Ciach definiują fazę jako "makroskopowo jednorodny stan układu, odpowiadający danym parametrom termodynamicznym." [6]. Dalej: "Proces przekształcania się jednej fazy w inną nazywa się przejściem fazowym lub przemianą fazową". Różne fazy mogą ze sobą współistnieć (stąd często w przejściach między jesienią a zimą oraz zimą i wiosną utrzymuje się temperatura 0 stopni), ale w przypadku ciągłych przejść fazowych, jedna faza przechodzi bezpośrednią w inną. "Ciągłe przejścia fazowe mają na ogół charakter przemiany typu porządek-nieporządek. Przemianą tego typu jest np. przejście paramagnetyk-ferromagnetyk, występujące w materiałach magnetycznych, takich jak żelazo. Uporządkowanie dotyczy tutaj mikroskopowych momentów magnetycznych umiejscowionych w węzłach sieci krystalicznej. W fazie paramagnetycznej orientacje momentów magnetycznych są chaotyczne, więc jeśli nie ma zewnętrznego pola magnetycznego, to magnetyzacja układu znika. Jest tak wówczas, gdy temperatura układu jest wyższa od pewnej charakterystycznej temperatury Tc, zwanej temperaturą Curie. Natomiast w temperaturze niższej od Tc, mikroskopowe momenty magnetyczne porządkują się spontanicznie wzdłuż pewnego wspólnego kierunku, i magnetyzacja przyjmuje wartość różną od zera. Istotne jest to, że magnetyzacja pojawia się spontanicznie, bez udziału zewnętrznego pola magnetycznego, jako efekt oddziaływania pomiędzy mikroskopowymi momentami magnetycznymi." Tak więc temperatura Curie to temperatura krytyczna dla przemian magnetycznych, która charakteryzuje jednocześnie obszar krytyczny.

Kutner pisze, że w obszarze krytycznym większość wielkości fizycznych zmienia się w zależności od temperatury T według prawa potęgowego:

(5)

gdzie Tc to temperatura krytyczna.

Aby zastosować pojęcie temperatury krytycznej do rynku, zastąpimy temperaturę T czasem t. Jest to chyba najważniejszy moment w zrozumieniu zastosowania fizyki do giełdy: temperaturę określamy jako wielkość proporcjonalną do czasu.

Punkt 1, który jest czysto matematyczny, wydaje się zupełnie logiczny, ale zawiera założenie, że szukamy tylko rozwiązania osobliwego (a nie ogólnego). To założenie jest potrzebne, aby spełniona została interpretacja fizyczna z pktu 2, mianowicie istnienia temperatury krytycznej, a więc dla ekonofizyki - czasu krytycznego. Natomiast czas krytyczny jest potrzebny po to, aby spełniona została koncepcja "racjonalnej (lub ograniczenie racjonalnej) bańki spekulacyjnej".

Technicznie rzecz biorąc zmienna (t - tc) stanie się ujemna, bo wielkość tc z założenia ma być większa od każdego t w którym operujemy: model ma prognozować przyszłość, a nie przeszłość. Dlatego od razu użyjemy zmiennej -(t-tc) = (tc - t). Następnie, nie interesuje nas za bardzo wykres z argumentami tc-t, bo przecież chcemy widzieć normalny przebieg czasu na wykresie. Punkt krytyczny tc jest parametrem do oszacowania, a więc stałą. Dlatego stworzymy zmienną P(t) zamiast P(tc - t). Stąd za P(tc - t)  podstawimy P(t). Jeżeli uprościmy szereg Fouriera w (4) do pierwszego rzędu, dostaniemy w końcu model log-periodyczny:

(6)

gdzie A, B, C, d to pewne stałe oraz

(7)

Do oszacowania parametrów zastosuję NMNK w Gretlu, której praktyczne zastosowanie szczegółowo opisałem w poprzednim artykule
Nieliniowa metoda najmniejszych kwadratów dla modelu trendu. Algorytm Levenberga–Marquardt może w końcu przydać się do czegoś praktycznego, bo poprzednie modelowanie trendu nieliniowego za pomocą funkcji wykładniczej, jak pokazałem, nie ma większego sensu. W przypadku skomplikowanych nieliniowych trendów z cyklami i krachami sprawa wygląda zupełnie inaczej. Tak więc algorytm jest analogiczny do tamtej funkcji. Algorytm Levenberga–Marquardt został także użyty przez Sornette'a i Sammisa [7], którzy jako jedni z pierwszych używali modelu (6) - ich pierwsze próby dotyczyły przewidywania trzęsień ziemi.

Kiedy zacząłem testować (6) szybko okazało się, że wiele zależy od ustawienia początkowych parametrów: a, d , w i tc. Algorytm wprawdzie sam je szacuje, ale potrzebuje danych wejściowych. W wielu sytuacjach model nie zbiega do wybranej funkcji. Stąd warto posłużyć się wynikami uzyskanymi przez innych badaczy. Drożdż, Grummer, Ruf i Speth [8] empirycznie dowodzą, że dla większości znaczących, historycznych finansowych zdarzeń, preferowana wartość parametru L = 2. Na podstawie wzoru (7) dostaniemy więc, że preferowane w równa się ok. 9,06. Następnie, w [9] autorzy stwierdzają, że jeśli 0 < a < 1, to cena w skończonym czasie dojdzie do tc. I jeszcze na koniec znalazłem jedną z najnowszych publikacji Sornette'a i Filimonova [10], którzy po zebraniu wielu danych, skompilowali parametry do następujących ograniczeń:
0.1 ≤ a ≤ 0.9,
6 ≤ w ≤ 13,
|C| < 1
B < 0.

Jeśli chodzi o ostatnią nierówność, to jest prawdopodobne, że B > 0 dla trendu spadkowego - znalazłem w [11]. Piszę prawdopodobnie, bo autor popełnił tam błąd we wzorze na w, więc nie mam pewności czy gdzieś indziej nie ma błędu.

Jeśli chodzi o początkowe tc, to jak sądzę preferowane będzie T+e gdzie T to liczba obserwacji, a e to liczba dni, po której spodziewalibyśmy się załamania (lub ewentualnie zmiany bessy na hossę) od momentu T.

Modele log-periodyczne w trzech ostatnich wspomnianych pracach opierają się na logarytmach ceny, czyli mają postać:

(8)

Tego właśnie modelu użyję.


Przykład 1. WIG: notowania dzienne 1994-13.01.2017 (T = 5704 obserwacji). Przy preferowanych parametrach modelu nie mogłem otrzymać. Dopiero po wpisaniu następujących wstępnych parametrów:
A = 1, B = -1, C = 0.5, a = 0.5, w = 15, d = -1, tc = 5800 uzyskałem model:

 Oszacowane tc = 7405,03 (p-value 1%). Z tego punktu widzenia krach nam nie straszny: 7405 - 5704 = 1701 dni pozostało do ewentualnego krachu. Jest to oczywiście tak odległa perspektywa, że nie ma sensu brać tego na poważnie. 

Zamiast tego cofnijmy się do końca czerwca 2007. Liczba danych = 3316. Ustawione preferowane początkowe parametry wystarczyły: A = 1, B = -1, C = 0.5, a = 0.5, w = 9.06, d = -1, tc = 3317. Tym razem model robi wrażenie:

Otóż oszacowane tc wyniosło 3321,68 (p-wartość 1%). Natomiast faktyczna bessa zaczęła od 3322 dnia (7.07.2007). Trafiło w punkt. W momentu prognozy do oszacowanego dnia załamania pozostało 5-6 dni (3321,68 - 3316).
Wydawałoby się, że potrafimy przewidywać przyszłość. Nie do końca. Gdy ustawimy dane do końca maja (3296 danych), to dostaniemy tc = 3301,19, czyli o 20 dni za wcześnie, ale 5 dni od dnia, w którym dokonalibyśmy prognozy (3301-3296=5). To samo, gdy ustawimy datę końcową koniec kwietnia (3275): dostaniemy tc = 3282,11. Tym razem jednak czas do prognozowanego krachu jest nieco większy (3282-3275=7 dni). Weźmy jeszcze koniec grudnia 2006 (3192 danych). Dostałem tc = 3213,42. Czas do szacowanego krachu jest znacznie większy (3213-3192=21 dni).

Zwracam uwagę, że nie ma znaczenia jaką ustawimy datę początkową tc, zawsze wyjdzie to samo. Odpowiednia wstępna wielkość tc jest potrzebna tylko po to, by algorytm "załapał" ten parametr. W powyższych przykładach najczęściej wpisywałem tc = T+1.

Tak więc decydującym jest ciągła aktualizacja modelu (8), tak jak wcześniej podkreślali to Sornette i Johansen. A mimo to możemy uzyskiwać fałszywe sygnały, o czym przekonamy się, generując prognozę w dniu poprzedzającym początek bessy, czyli 6.07.2007: znów przesunęłaby się prognoza krachu o ok. 5-6 dni (T = 3321 oraz tc wyniósłby 3326,6, czyli 3326,6-3321=5,6). Ta sytuacja będzie codziennie się powtarzać, przez cały lipiec, a nawet w kolejnych miesiącach.

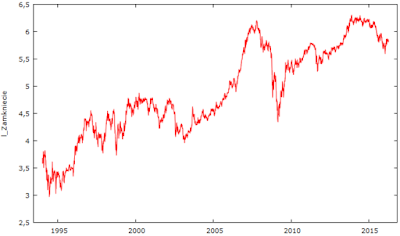
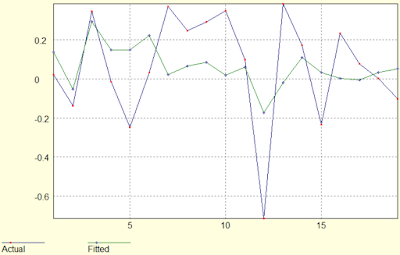
Przykład 2. Mbank: roczne 1994-2015 (T = 22 obserwacje). Wróćmy jeszcze raz do mbanku, który ostatnio modelowałem regresją nieliniową, tyle że zwykłą funkcją wykładniczą. Tym razem możemy znaleźć o wiele dokładniejsze przewidywania przy tych samych danych. Aby dostać model użyłem: A = 1, B = -1, C = 0.5, a = 0.5, w = 16, d = -1, tc =23. NMNK oszacował tc = 24,87, a wykres jest taki:

Jednakże obecnie możemy już dodać rok 2016. Pytanie czy wielkość tc zmieni się? Użyłem tych samych wstępnych parametrów. NMNK oszacował ponownie tc = 24,87, a wykres jest taki:

 Czyli wg modelu mamy spodziewać się załamania za 1-2 lata.

Aby jednak nie napawać się zbytnio optymizmem, pokażę teraz, że model (8) kiepsko radził sobie z dziennymi wahaniami.


Przykład 3. Mbank: dzienne 1994-koniec 2013 (T = 4941 obserwacji): Wpisałem następujące wstępne parametry:
A = 1, B = -1, C = 0.5, a = 0.5, w = 9.06, d = -1, tc = 5000. Uzyskałem model o wykresie:

Ogólnie model na rysunku wydaje się całkiem dobry. Parametr krytyczny tc został oszacowany na 5507,77 i jest istotny statystycznie na poziomie 1% (tak samo jak reszta parametrów). czyli krachu powinniśmy oczekiwać po 5507,77-4941 = 566,77 dniach. Dodatkowo: Błąd standardowy reszt  = 0,252757, Skorygowany R-kwadrat   0,890034. Co więc się stało po tym czasie? Poniżej zamieściłem ten sam wykres powiększony o 567 dni.

A do dziś mamy:

Już dawno po "krachu". Model powinien przewidywać go w momencie gdy tworzyliśmy prognozę, bo od tego momentu trend się zmienił. Ale można byłoby starać się obronić model, bo kurs od momentu wykonania prognozy, czyli końca 2013, przez kolejne pół roku stał w miejscu, więc należałoby aktualizować model i być może wtedy uzyskalibyśmy moment wyjścia? Nic z tego. Przesuwając dane do końca lipca 2014 (5087) dostaniemy tc = 5588,87 i wykres:

Zatem czekalibyśmy, bo przecież różnica 5589-5087 = 502, czyli jeszcze ok. 2 lata dni roboczych.

Powyższe bardzo skrótowe testy pokazały, że model log-periodyczny może rzeczywiście służyć jako wskaźnik "temperatury rynku" czy zwiększonej niepewności dla racjonalnego inwestora, tak że spekulacja zaczyna przeważać nad wyceną fundamentalną. Ale kontrowersyjne jest twierdzenie, że pozwala przewidywać zmianę trendu. Możliwe, że rynek zachowuje się tak jak to opisuje teoria Sornette-Johansena [2, 3, 4]. Fakt pozostaje faktem, że analiza WIG wykazała, że im bliżej był dzień zmiany trendu w 2007, tym model (8) wskazywał na coraz bliższą datę od momentu prognozy, przy czym krańcowym czasem pozostałym do załamania był mniej więcej 1 tydzień.

Na sam koniec stworzę prognozę dla indeksu USA dla częstości rocznej i miesięcznej.

Przykład 4. S&P500 roczne: 1933-2016 (T=84 dane). Wstawiłem standardowe parametry, w tym tc = 85. W odpowiedzi otrzymałem tc = 94,355. Czyli do krachu stulecia jeszcze 10 lat.

Najgorsze rezultaty model osiągnął w drugiej połowie lat 90 XX w. Można to nawet potraktować jako argument za przewartościowaniem akcji w tym okresie.

Przykład 5. S&P500: miesięczne 1933-koniec 2016 (T=1008). Ustawienia: identyczne co poprzednio, ale nie chciało wejść z tc = 1009 i dopiero dla tc = 1020 "załapało". Prognoza tc = 1126,55, a wykres przedstawia się:

W powiększeniu ostatnich okresów widać, że model wchodzi w fazę wzrostu:

Jeżeli prognoza się sprawdzi, to czeka nas krach w USA za 119 miesięcy, czyli za 119/12 = 9,9 lat. Prognoza miesięczna idealnie więc pokrywa się z prognozą roczną.


Literatura:
[1] Sornette, D., Johansen, A. - Modeling the stock market prior to large crashes, 1999,
[2] Sornette, D., Johansen, A. - Critical Market Crashes, 1999,
[3] Sornette, D., Johansen A., Ledoit, O. - Predicting Financial Crashes Using Discrete Scale Invariance, Feb 2008,
[4] Sornette, D., Johansen A. - Significane of log-periodic precursors to financial crashes, Feb. 1, 2008,
[5] Kutner, R., Wprowadzenie Do Ekonofizyki: Niegaussowskie Procesy Stochastyczne Oraz Niedebye'Owska Relaksacja W Realu. Elementy teorii ryzyka rynkowego wraz z elementami teorii zdarzeń ekstremalnych, W-wa czerwiec 2015,
[6] Hołyst, R., Poniewierski A., Ciach A., Termodynamika Dla Chemików, Fizyków I Inżynierów, Październik 2003,
[7] Sornette, D., Sammis, C., - Complex critical exponents from renormalization group theory of earthquakes Implications for earthquake predictions, 1995,
[8] Drożdż S., Grummer, F., Ruf, F., Speth, F. - Log-periodic self-similarity an emerging financial law, 2002,
[9] Fantazzini, D. ,Geraskin, P., - Everything You Always Wanted to Know about Log Periodic Power Laws for Bubble Modelling but Were Afraid to Ask, Feb 2011,
[10] Sornette, D., Filimonov, V. - A Stable and Robust Calibration Scheme of the Log-Periodic Power Law Model, 2013,
[11] Górski, M. - Zastosowanie Teorii Log-Periodyczności W Prognozowaniu Krachów Giełdowych, 1/2014.

Nieliniowa metoda najmniejszych kwadratów dla modelu trendu

W wielu pakietach ekonometrycznych można użyć Nieliniowej Metody Najmniejszych Kwadratów (NMNK), aby uzyskać bezpośrednio poszukiwany parametr. NMNK ma podobnie jak MNK podstawy teoretyczne - o ile słuszność MNK wynika z twierdzenia Gaussa-Markowa, o tyle NMNK jest słuszna z powodu uogólnionych twierdzeń Gaussa-Markowa [1, 2, 3], a także dowiedzionej asymptotycznej zgodności jej estymatora [4].

NMNK nie jest jednolitą metodą. W Gretlu stosowany jest algorytm Levenberga–Marquardt. Algorytm ten jest kombinacją dwóch znanych metod numerycznych: metody gradientu prostego oraz algorytmu Gaussa-Newtona. W metodzie gradientu prostego suma kwadratów błędów jest korygowana w kierunku spadku nachylenia funkcji (gradientu), bo tam znajduje się minimum. W metodzie Gaussa-Newtona wykorzystuje się z kolei przybliżenie funkcji za pomocą wzoru Taylora; kwadraty różnic pomiędzy prawdziwą funkcją a funkcją Taylora powinny być jak najmniejsze [5].

Na chwilę zostawmy to. Wcześniej (tu oraz tu) pokazałem, jak poprawnie retransformować model trendu, aby uzyskać warunkową oczekiwaną stopę zwrotu. Mamy następujący model trendu:

(1)

Powinniśmy zdefiniować składnik losowy. Powiedzmy, że jest on stacjonarny, posiada wartość oczekiwaną = 0 oraz stałą wariancję. Jeżeli zmienna losowa P(T) ma rozkład log-normalny, to jej wartość oczekiwana wynosi:

(2)

Dzięki NMNK możemy oszacować parametry bezpośrednio z modelu (1), a więc bez potrzeby transformacji logarytmicznej. Przykładowo, biorąc te same dane dla mbanku co w wymienionych na początku artykułach (rocznie 1994-2015; 22 obserwacje), możemy stworzyć w Gretlu model (1). Po zaimportowaniu danych, trzeba kliknąć: Model -> Nieliniowa Metoda Najmniejszych Kwadratów. Pojawi się okno i tam wpisujemy:
.................
scalar a = 1
scalar b = 1
Zamkniecie = exp(a+b*time)
deriv a = exp(a+b*time)
deriv b = exp(a+b*time)*time
.................

gdzie:
Zamkniecie - to szereg czasowy, w naszym przypadku kurs mbanku (zmienna P(T));
time - zmienna czasowa (wygenerowana w opcji Dodawanie zmiennych -> time - zmienna czasowa.
a, b - współczynniki regresji, które trzeba od początku zadeklarować. Są to skalary w naszej funkcji, które przyjmą jakąś początkową wartość, np. 1. Standardowo deklarujemy więc scalar a = 1, scalar b = 1. Mogą być one dowolne, ale może się zdarzyć, że nie wystarczy iteracji, aby zbiegły do prawdziwej wartości wg algorytmu. Jeśli tak się stanie, zmieniamy metodą prób błędów.

deriv - pochodna funkcji po danym współczynniku. Np. pochodna d(Zamkniecie)/d(a) = exp(a+b*time), dlatego jest zapis:
deriv a = exp(a+b*time).
I tak samo dla b: pochodna d(Zamkniecie)/d(b) = exp(a+b*time)*time. Dlatego jest zapis:
deriv b = exp(a+b*time)*time.

Mimo że a i b są to skalary modelu, to są one w funkcji szacowane, czyli pierwotnie są zmiennymi.

Niezbyt przyjemne. Można się obyć bez pochodnej, ale w helpie Gretl rekomenduje jej obliczanie.

Przed kliknięciem OK, możemy zaznaczyć jeszcze opcję "Odporne błędy standardowe". Wtedy OK.

Jak widać na tablicy zbieżność nastąpiła po 27 iteracjach. Gdybyśmy wpisali scalar a = 10, scalar b = 10, zbieżność nastąpiłaby dopiero po 240 iteracjach.

Uzyskany parametr b = 0,0996, natomiast wolny parametr a możemy zignorować, bo interesują nas stopy zmian. W porównaniu do logarytmicznego modelu, gdzie uzyskaliśmy logarytmiczną stopę ponad 11%, może się wydać dziwne, że teraz jest niższa wartość. Przecież otrzymaliśmy od razu stopę, która powinna być właśnie wyższa od tej z modelu logarytmicznego MNK. Co jest tego przyczyną? Stało się tak, bo nasz model jest niepełny. Założyliśmy błędnie, że wygląda jak na poniższym rysunku:

W tym modelu składnik losowy jest stacjonarny, może więc to być zmienna losowa o rozkładzie normalnym. Ta zmienna po prostu jest argumentem funkcji wykładniczej. Ale w rzeczywistości powinna być funkcją czasu. Gdy za tę zmienną losową wstawimy proces Browna, czyli skumulowaną zmienną losową o rozkładzie normalnym, to otrzymamy geometryczny proces ruchu Browna. Wtedy nasz model wygląda mniej więcej tak:

Ogólnie geometryczny proces ruchu Browna ma postać (zob. np. [6]):

(3)

gdzie B(T) jest zwykłym procesem ruchu Browna. B(0) = 0.

Proces (3) w danym punkcie czasu może przyjąć różne wartości zgodnie z pewnym rozkładem prawdopodobieństwa. Przestaje być więc rozumiany jako proces, a staje się "ruchem" - zmienną stacjonarną. Ten ruch posiada zawsze rozkład log-normalny. Oznacza to, że możemy wyprowadzić analogicznie do (1) wartość oczekiwaną tej zmiennej.

Zauważamy, że składnik losowy w modelu (1) to jest to samo co (odchylenie standardowe razy proces ruchu Browna) w modelu (3), co oznacza, że musi się tak samo przekształcać jak w modelu (2), gdzie występuje wartość oczekiwana procesu. I stąd podstawiając do (3) powyższe wyprowadzenie wariancji, dostaniemy wartość oczekiwaną geometrycznego (procesu) ruchu Browna:

(4)

W tym miejscu rodzi się pytanie czy rzeczywiście znamy wartość początkową P(0). To zależy od tego czy zaczynamy od T = 1 czy T = 0. Musimy zdecydować czy pierwsza wartość już decyduje o funkcji zależnej od czasu czy dopiero kolejna. Jeśli założymy, że P(0) jest znane, to podstawimy pierwszą cenę zamknięcia mbanku z 1994 r., czyli 30, 68. W przeciwnym wypadku P(0) musi zostać oszacowane. Wybór sposobu ma istotne znaczenie dla uzyskanych wyników: dodanie wolnego wyrazu zmienia postać modelu. Ale jeżeli wybierzemy model z wyrazem wolnym, to estymacja NMNK przyniesie ten sam rezultat co dla modelu (2) - czyli powracamy do modelu (1), który przecież uznaliśmy za niepełny. Wstawienie P(0) nie rozwiąże tego problemu, ale możemy sprawdzić do czego doprowadzi.

Wstawiamy pierwszą cenę zamknięcia P(0) = 30,68. Możemy wtedy powtórzyć całą procedurę w Gretlu, używając modelu (4):

.................
scalar b = 1
Zamkniecie = 30.68*exp(b*time)
deriv b = 30.68*exp(b*time)*time
.................

Uzyskane parametry to:

Dostaniemy wykres trendu:

Zatem u = 12,5, czyli efektywna oczekiwana stopa exp(12,5) - 1 = 13,3%.

Mimo iż obliczyliśmy parametr u, to taki estymator jest niezgodny w tym sensie, że nie będzie dążył do prawdziwej wartości parametru u. Żeby była zgodność, składnik losowy musi być stacjonarny (zob. twierdzenia w [4]). Najprawdopodobniej potrzeba użyć uogólnionej nieliniowej metody najmniejszych kwadratów, która pozwoliłaby uwzględnić rosnącą wariancję i autokorelację składnika losowego.

Ostatecznie można ten problem rozwiązać. Łatwo zauważyć, że tylko w punkcie dla T = 1 geometryczny proces ruchu Browna będzie tożsamy z modelem (1), dla którego składnik losowy jest stacjonarny. W tym punkcie obydwie krzywe się przetną. Czyli w tym punkcie model (2) równa się modelowi (4):

Wyrazy wolne możemy do siebie dostosować, aby zachować identyczną interpretację punktu startu. Dlatego przyjmiemy lnP(0) = a. Stąd:

(5)

Ze względu na stacjonarność składnika losowego dla T = 1 estymator u równy b plus połowa wariancji może stać się w końcu zgodny. Wcześniej oszacowany współczynnik b był estymatorem zgodnym (zakładaliśmy początkowo stacjonarność składnika losowego), chociaż występował w modelu niepełnym. Połowa wariancji też jest estymatorem zgodnym. Suma estymatorów zgodnych daje estymator zgodny (wynika to z własności granicy ciągów). Stąd parametr u równy b plus połowa wariancji stanie się estymatorem zgodnym. Parametr b został wcześniej oszacowany, ale wariancję również znamy, bo jest to przecież ten sam składnik, który był obliczany dla MNK. Estymowaliśmy go wcześniej za pomocą błędu standardowego reszt (tu) i wyniósł 0,346. Możemy podstawić:

u = b + 0,5var
u = 0,0996 + 0,5*0,346^2 = 0,1596

Aby uzyskać oczekiwaną (efektywną) stopę zwrotu wstawimy exp(0,1596) - 1 = 17,3%. Dla porównania w Transformacja lognormalnego modelu z nieznanym parametrem wyszła wartość zbliżona, bo 18,7%.

Literatura:
[1] Louton, T., The Gauss-Markov Theorem for Nonlinear Models, Dec. 1982,
[2] Kariya, T., A Nonlinear Version of the Gauss-Markov Theorem, Jun. 1985,
[3] Kariya, T., A Maximal Extension of the Gauss–Markov Theorem and Its Nonlinear Version, 2002,
[4] Wu, C-F, Asymptotic Theory of Nonlinear Least Squares Estimation, May 1981,
[5] Marquardt, D. W., An Algorithm for Least-Squares Estimation of Nonlinear Parameters, Jun. 1963.
[6] https://en.wikipedia.org/wiki/Geometric_Brownian_motion

Wolność mediów jest zła

Janusz Korwin-Mikke napisał na swoim blogu kilka lat temu w 2011 roku [1]:
"Jestem libertarianinem nie tylko w dziedzinie gospodarczej. Idę znacznie dalej: uważam, że człowiek powinien mieć prawo DZIAŁAĆ jak chce – byle nie szkodził innym – bo tylko on może ocenić, co jest dla niego dobre. Natomiast wcale nie uważam, że człowiek powinien mieć prawo GADAĆ, co chce… W każdym razie nie w mass mediach. Bo tam najczęściej szkodzi! Dlaczego?"

Ogólnie zgadzam się z tym stwierdzeniem, ale mam 4 zastrzeżenia, o których powiem.

Po pierwsze Korwin Mikke błędnie oddziela sferę idei od sfery gospodarczej. Mikke wprawdzie argumentuje ten podział, stwierdzając, że "nie istnieją „banki idej”, skąd za opłatą pobierałoby się ideę i sprzedawało ją komuś… Wtedy istotnie lepsza wypierałaby gorszą.". W rzeczywistości informacja to też jest dobro, które się kupuje i sprzedaje. Np. S. Hawking w książce "Krótka historia czasu" napisał we wprowadzeniu, że na początku ostrzegano go, że z każdym kolejnym wzorem zamieszczonym w swojej książce liczba sprzedanych egzemplarzy spadnie o połowę. A skoro popularyzacja nauki musi polegać na uproszczeniach i mieć formę przystępną dla laika, to znaczy, że dzieje się coś wręcz przeciwnego niż mówi Mikke: "lepsze", tj. dokładne przekazanie idei jest wypierane przez to "gorsze". Użyłem cudzysłowu, bo w przypadku światowej sławy profesora napisanie książki popularno-naukowej zawsze będzie miało wysoką wartość i jakość. Ale dlaczego tak się dzieje? To proste: mało jest osób, które byłyby w stanie zrozumieć (nie mówiąc już o chęci) wywód naukowy, a więc i popyt byłby niski, co obniżałoby cenę. To jest po drugie.

A teraz zauważmy, że w codziennym życiu występuje analogia: prasa przekazuje ludziom wiadomości w taki sposób, aby JAK NAJWIĘCEJ ludzi je przeczytało, obejrzało lub wysłuchało. Aby tak się stało, informacje muszą mieć prosty i jasny przekaz, a tytuł musi być donośny lub kontrowersyjny. Dziennikarze, którzy piszą, np. o nowych odkryciach naukowych, zapewne często głowią się jak zebrany materiał tak uprościć, aby z jednej strony przekazać nić przewodnią, z drugiej aby nie wdawać się w szczegóły. Ale - jeśli czegoś nie wystarczająco dobrze zrozumieją - to łatwo popełnią błąd merytoryczny.

Dziennikarz, który jest przecież pośrednikiem pomiędzy przedsiębiorcą (wydawcą) a konsumentem informacji, nie musi mieć wykształcenia w danej dziedzinie nauki, jednakże musi mieć umiejętność odpowiedniego ubrania trudnych rzeczy w przystępne dla przeciętnego odbiorcy słowa.

Jeżeli dziennikarz wykonuje swoją profesję sumiennie i stara się być obiektywny, to popełniane błędy, jeśli zostaną skorygowane, zostaną wybaczone. Gorzej jeśli dziennikarz ma pewien określony pogląd, który jest przez naukowców podważany lub poddawany w wątpliwość. Oczywiście nie jest niczym złym, jeśli dziennikarz ma poglądy lewicowe lub prawicowe i przemyci do swojego artykułu swoje wątpliwości co do jakiejś reformy czy ustawy - pod warunkiem, że zachowuje obiektywizm w przedstawianiu faktów. Ale w którymś momencie jego poglądy, mogą wychodzić coraz bardziej na powierzchnię, aż w końcu całkowicie przyjąć tylko punkt widzenia jednej strony i dezawuować punkt widzenia drugiej strony, np. przedstawiać tylko argumenty jednych, a pomijać fakty na korzyść drugich.

W ten sposób zaczyna rodzić się propaganda. Takie media, czyli mediatorzy, czyli pośrednicy, są oszustami. Ludzie płacą za gazetę albo obejrzą reklamę, aby mieć dostęp do informacji. Od tego momentu zaczyna się problem. Bo ludzie mogą "kupować" informacje z dwóch pobudek:
A) mogą chcieć dowiedzieć się nowych rzeczy, z czystej ciekawości albo z jakiejś innej potrzeby (np. jakiejś porady). Liczą na to, że przeczytają prawdę.

B) mogą kupować informacje tylko po to, aby móc coś lub kogoś skrytykować. Krytyka ta może przyjąć różne formy: wewnętrznego lub zewnętrznego "hejtingu" albo trollowania na forach. Ta krytyka często przyjmuje formę tzw. "mowy nienawiści". W tym przypadku nie liczy się prawda, właściwie treść nie ma znaczenia, bo i tak jest wykorzystywana jako pretekst do zaatakowania danego podmiotu. A jeżeli autor artykułu czy przemówienia nie spełni ich oczekiwań, to atakują samego autora. Jeżeli natomiast autor przedstawi zamiast prawdziwego obrazu sytuacji jedynie jego własną interpretację, to taki autor będzie chwalony.

Zauważmy do czego to prowadzi. Ludzie z (B) czytają albo słuchają tylko takich portali, które zaspokajają żądze "dokopania" komuś oraz takich, których należy dla zasady skrytykować. A skoro jest na nie popyt, to będzie rodziła się podaż i w ten sposób wyłania podział na dwa antagonistyczne rodzaje mediów.

Gdyby istnieli tylko ludzie z (B), nie byłoby żadnego problemu. Ale kłopot polega na tym, że ludzie (A) są pokrzywdzoną stroną w tym konflikcie. A przecież zgodziłem się ze stwierdzeniem Korwina Mikke, że ludzie mogą robić co chcą, dopóki nie szkodzą innym. Wprawdzie nikt nie każe czytać (A) kłamliwych bądź przeinaczonych wypowiedzi, ale chodzi o to, że treść jest wystawiona na pokaz, która może dotrzeć do mniej świadomej osoby czy to w internecie przez przypadek, czy w innym medium, za które jeszcze zapłaciła.
Stąd płynie logiczny wniosek, że pełna wolność mediów jest zła. 

Dlatego jedną z roli państwa powinno być dbanie o jakość informacji przekazywanych przez media dokładnie na tej samej zasadzie jak kontrolowana jest żywność w sklepach. Oczywiście tylko przez naukowców. Kontrola powinna odbywać się w specjalnych warunkach, do których politycy ogólnie nie powinni mieć wstępu. Jeżeli byłyby to informacje ekonomiczne, to kontrolą powinni zajmować się tylko ekonomiści.

Nie byłby to świat, w którym każda napisana notatka na Twitterze byłaby analizowana przez sztab naukowców. Są tutaj dwie drogi.
1) wybieranie do badań statystycznych próbek
2) działanie podobne jak w wikipedii (połączenie weryfikowania źródeł przez niekoniecznie specjalistów w danej dziedzinie oraz przez sztuczną inteligencję, zob. np. tutaj)

Nie będę wdawał się w szczegóły co zrobić, kiedy już taka instytucja odkryje fałszywe informacje na jakiejś stronie. Jasne jest, że jeśli będą podawane przez oficjalny podmiot (np. dziennikarzy), to kary powinny być surowsze. Np. najpierw polecenie usunięcia, a potem jeśli podobne zdarzenie się powtórzy, jakieś kary finansowe. W przypadku użytkowników anonimowych również powinny być wysyłane ostrzeżenia, a po pewnym czasie - jeśli nie byłoby poprawy - sprawa powinna trafić do prokuratury itd.

Pytanie co zrobić w sytuacji, gdy ktoś napisze ostrą satyrę na temat rządu. Wiadomo, że to jest fikcja literacka, nawet jeśli zawiera wydarzenia i postaci prawdziwe. I tu pojawia się trzecie moje zastrzeżenie w cytacie Korwina Mikke. Stwierdził on, że publiczne słowa nie powinny szkodzić innym. Otóż ostra satyra, parodia czy groteska szkodzi rządowi. Ale jest społecznie pożyteczna. Dlatego zdanie to powinno zostać doprecyzowane i na przykład słowo "innym" zastąpić "społeczeństwu". Co natomiast w przypadku jakiegoś antyrządowego bloga? Ogólna zasada powinna być taka, że dopóki autor wyraża tylko swój pogląd, którego nie można zweryfikować, bo nie dotyczy sfery nauki, to może pisać bloga. Jeżeli jednak zaczyna mieszać politykę z ekonomią i np. głosi, że program 500+ przyniesie co roku 1 pkt proc. wzrostu PKB, to należy bezwzględnie kazać mu usunąć takie herezje.

Czwarte moje zastrzeżenie dotyczy już wniosków całego tekstu. Otóż Korwin Mikke wydaje się bronić ustawy medialnej Orbana na Węgrzech, którą z kolei krytykuje inny publicysta J. Woziński. Cytując Wozińskiego, zgodnie z tą  ustawą "35% muzyki granej w radiach ma stanowić muzyka węgierska, połowa programów telewizyjnych musi być produkcji europejskiej, a jedna trzecia z nich – węgierskiej" [2]. Nie trudno zrozumieć Mikkego, że woli, aby społeczeństwo było wychowywane w duchu kultury wyższej, zamiast chłamu amerykańskiego. Problem polega na tym, że w ten sposób zabiera się wybór konsumentom. Przecież gdyby nie chcieli słuchać i oglądać tego chłamu, toby nie oglądali, a wtedy media musiałyby zmienić repertuar. Ale oglądają, bo przecież "większość jest głupich niż mądrych", cytując JKM. Zatem gdyby media zostały zmuszone do puszczania codziennie filmów Felliniego czy Antonioniego zamiast "Rambo", to ludzie przestaliby oglądać telewizję i zysk prywatnych stacji spadły, a może nawet zamieniłby się w stratę. PKB spadłoby. Do takiego efektu doprowadziłby centralny plan wyższej kultury Mikkego. Przecież komunizm i socjalizm zbankrutował dlatego, że właśnie ograniczał wybór jednostki.

Zupełnie inny charakter mają media publiczne. To właśnie ich rolą powinno być krzewienie wyższej kultury, a także stawianie na jakość podawanej informacji, stanowiąc przeciwwagę dla mediów komercyjnych. Dlatego takie ustawy powinny być ustawami tylko mediów publicznych.

Na koniec, już tylko dla refleksji, ponieważ ostatnie dni - piątek, sobota 16-17.12.2016 - obfitowały w najbardziej emocjonujące wydarzenia w polskiej polityce od wielu lat (zakończone zamieszkami protesty pod sejmem spowodowane dążeniem przez PIS do ograniczenia swobody obserwowania sejmu przez dziennikarzy), przytoczę inny fragment cytowanego powyżej artykułu Wozińskiego z 5 stycznia 2011 r. [2]:
"Posunięć węgierskich konserwatywnych purytanów nie można niestety uznać za przypadek odosobniony. O podobnych zarządzeniach marzą w wielu innych krajach rozmaite typy Kaczyńskich i Orbánów, którym jednak nie poszczęściło się nigdy na tyle, aby wygrać wybory z wynikiem 53% głosów. Gdyby w Polsce malowana prawica spod znaku PiS uzyskała kiedykolwiek podobny wynik, mielibyśmy zapewne do czynienia (z zapowiadaną przecież wielokrotnie) falą idiotycznych ustaw w rodzaju Nowego Medialnego Ładu, nacjonalizacją przedsiębiorstw o „strategicznym znaczeniu dla narodu”, zakazami określonych manifestacji, likwidacją sex shopów itd., itp."


Źródło:
[1] Korwin-Mikke: Zasada ograniczania wolności mediów nie jest zła!, http://nczas.com/wiadomosci/polska/korwin-mikke-zasada-ograniczania-wolnosci-mediow-nie-jest-zla/
[2] Prawdziwe arcydzieło pobożnego i purytańskiego socjalizmu ma Węgrzech, http://nczas.com/wiadomosci/europa/absurdalne-purytansko-nacjonalistyczne-zmiany-w-wegierskiej-telewizji/

Współczynnik Kaitza jako predyktor giełdy?

Zgodnie z hipotezą efektywnego rynku wszelkie informacje mające wpływ na wartość aktywa są uwzględnione przez cenę rynkową tego aktywa natychmiast po ich ujawnieniu się. Oznacza to, że jeśli np. teraz pojawia się informacja o stanie gospodarki, to za moment zostanie ona zdyskontowana przez giełdę. W ostatnich 3 artykułach wskazywałem na prace sugerujące negatywny wpływ płacy minimalnej (PM) na gospodarkę poprzez wzrost bezrobocia albo inflacji. Np. Dańska-Borsiak [1] doszła do wniosku, że wzrost współczynnika Kaitza (WK), czyli stosunku płacy minimalnej do przeciętnej, zwiększa stopę młodych bezrobotnych z rocznym opóźnieniem. Jeżeli rynek jest efektywny, to ceny akcji powinny spaść natychmiast po informacji, że nastąpi wzrost WK. Nie ma więc znaczenia data wprowadzenia nowej PM, a tym bardziej nie powinno być żadnego wpływu po roku, gdy wystąpią już spadki inwestycji czy PKB.

Przetestowałem więc tę hipotezę, porównując zmiany logarytmicznego WIG ze zmianami logarytmicznego WK z opóźnieniem 1 roku dla Polski w latach 1995-2015 (20 obserwacji minus 1 z powodu opóźnienia). Dane roczne WIG wzięte ze stooq.pl, natomiast zmiany WK obliczyłem, wykorzystując strony Mpips , GUS. Okazuje się, że autokorelacja Pearsona między log-stopami WIG oraz log-stopami WK (ale tylko opóźnionego o 1 rok) jest ujemna i wynosi -0,375 przy p value  = 0,1132. Trzeba tu jednak zwrócić uwagę, że korelacja rang Spearmana wynosi 0, co sugeruje, że może nie chodzić tu o sam znak (kierunek) skorelowania skorelowania, ale o siłę. Następnie w Excelu zrobiłem klasyczną regresję liniową:

Jak widać p-value identycznie na poziomie 0,1132 wskazuje na bliską istotność na poziomie 10%. Średnia elastyczność wychodzi na poziomie -2,31, co oznacza w tym przypadku, że wzrost WK o 1 pkt proc. wywoduje średnią log-stopę WIG na poziomie -2,31% w następnym roku. Trzeba dodać jednak, że dopasowany R^2 jest poniżej 10%, co wskazuje, że model nie posiada mocy predykcyjnej. Porównać można to z wykresem, na którym zmienna opóźniona log-stopa WK(-1) stanowi wartość aktualną (actual), a log-stopa WIG wartość dopasowaną (fitted):

Wykres actual nie uwzględnia roku 2015, bo prognozowany kolejny rok 2016 jeszcze się nie skończył. Stąd dziś możemy prognozować stopę na 2016 i 2017. Na końcu roku 2015 log-stopa WK wyniosła ok. +2,5% (ln[WK(2015)/WK(2014)] = 2,5%; WK(2015) = 1850/3899,78 = 0,474; WK(2014) = 1750/3783,46 = 0,4625) lub inaczej log-WK wzrósł o 2,5%. Możemy prognozować, że pod koniec 2016 r. log-WIG spadnie o 2,5%*2,31 = 5,78%. Gdyby przekształcić to do zwykłej stopy, dostalibyśmy exp(-0,0578)-1 = -5,61%. Przypomnę jednak, że takie przekształcenie dostarcza tylko informacji o medianie (zob. Czy mediana jest lepsza od średniej?), a nie wartości oczekiwanej. Aby uzyskać wartość oczekiwaną stopy możemy posłużyć się estymatorem Duana dla dowolnego rozkładu, ale najlepiej by nie był lognormalny (zob. Smarujący estymator). "Smarujący estymator" Duana ma następującą postać:

(1)

 

Jest to minimalnie bardziej ogólna postać niż ta, którą podałem w artykule Smarujący estymator , bo tam czas był zmienną objaśniającą, która się redukowała po zamianie na stopę; smarujący estymator jest szczegółowo opisany w [2]. Sumę exp(składnik losowy(t)) uzyskałem w Gretlu. Podstawiam dane do (1):

Zatem powinniśmy oczekiwać, że WIG z końca 2015 spadnie o niecałe 3% na koniec 2016. Z dzisiejszego punktu widzenia oznacza to poziom ok. 45070 i od obecnego punktu (18.11.2016) prognozuje to ok. 4% spadku:

Dodatkowo policzmy jeszcze potencjalną zmianę w 2017. Ostatni komunikat GUS głosi, że płaca przeciętna wyniosła w 3 kw. 4055 zł. Zakładając, że na koniec 2016 r. będzie to 4060 oraz wiedząc, że od początku 2017 r. PM = 2000 zł, możemy obliczyć WK(2016) = 2000/4060 = 0,49. WK(2015) = 0,474, stąd ln(0,49/0,474) = 0,0332. Mediana zwykłej stopy będzie w takim razie wynosiła ok. exp(-0,0332*2,31)-1 = -7,38%. Gdyby założyć, że suma składników losowych jest taka sama jak w 2015, to podstawiając do (1) prognozowalibyśmy następującą oczekiwaną stopę zwrotu WIG w 2017:

Czyli przy takich założeniach WIG spadłby o kolejne 4,6%. Jednak tak jak wspomniałem, moc predykcyjna jest zbyt słaba by traktować poważnie taki model. Może jednak wskazywać siłę kierunku zmian cen: jeśli w jednym okresie WK rośnie, to w następnym WIG może wolniej wzrosnąć (czy po prostu spaść).


Warto jeszcze spojrzeć na profesjonalne prace, np. Bella i Machina, którzy wykorzystują tzw. analizę zdarzeń do oszacowania efektywności brytyjskiego rynku na wiadomość o podniesieniu PM [3]. Anomalną (abnormal) skumulowaną stopę zwrotu z akcji spółek, które zatrudniają pracowników na PM, autorzy porównali z teoretyczną stopą CAPM przed i po komunikacie. Wyniki pokazują, że w obydwu przypadkach wartości rynkowe istotnie spadały. W ciągu 10 dni od ogłoszenia ceny tych firm były niższe o ok. 3%. Zbiorowe wyniki przedstawia poniższa tabela:

 NMW - National Minimum Wage jest to zmienna sztuczna (dummy), która przyjmuje wartości 1 (firma zatrudnia wielu za PM) lub 0 (firma nie zatrudnia wielu za PM).
 Najważniejsza wydaje się tu kolumna (1) i (2). Wiersz NMW - Kolumna (1) wskazuje, że anomalna 15-dniowa stopa zwrotu wyniosła -2,6% i jest istotna na poziomie 1% istotności. Kolumna (2) uwzględnia dodatkowe czynniki (literka Y), jak np. wielkość spółki lub to czy przed ogłoszeniem nowej PM stopy spadały. Wtedy efekt nawet rośnie: firmy, które zatrudniają za PM, o prawie 4% tracą nadmiernie na wartości. Sytuację ilustruje poniższy wykres:

 
Podsumowując, można powiedzieć, że wpływ zmiany płacy minimalnej na rynek akcji jest istotnie negatywny, co więcej można przypuszczać, że stanowi jedną z anomalii rynku akcji, pozwalając prognozować spadek stóp zwrotu.


Literatura:

[1] B. Dańska-Borsiak, Płaca Minimalna A Liczba Młodych Pracujących. Związki Przyczynowe I Prognozy Wariantowe, Uniwersytet Łódzki, 2014,
[2] N. Duan, Smearing Estimate: A Nonparametric Retransformation Method, Sep. 1983,
[3] B. Bell, S. Machin, Minimum Wages and Firm Value, Nov. 2015.

Źródło danych:
http://stooq.pl/
http://stat.gov.pl/
http://www.mpips.gov.pl/

Większa płaca minimalna prowadzi do bezrobocia albo inflacji

W poprzednich dwóch artykułach wskazywałem na empiryczne dowody, że płaca minimalna (PM) nie stanowi żadnego rozwiązania problemu biedy. Po pierwsze zostało w wielu opracowaniach wykazane, że bezpośredni wpływ PM na poziom biedy najmniej zarabiających jest statystycznie zerowy. Po drugie podałem pracę dotyczącą polskiego rynku pracy, w której dowodzi się, że z rocznym opóźnieniem występuje dodatnia korelacja między wzrostem PM a liczbą młodych bezrobotnych oraz że przy wysokim stosunku PM do średniej krajowej (powyżej 40%) wpływ wzrostu płacy minimalnej jest szkodliwy dla polskiej gospodarki. W swojej książce Balcerowicz "Trzeba się bić z PIS o Polskę" stwierdził stanowczo, że dla niego PM jest przestępstwem, bo ogranicza zatrudnianie młodocianych. Jakby to nie nazwać, PM wyrządza więcej szkód niż pożytku. Politycy chcieliby zmusić przedsiębiorców do tego, aby swoim własnym kosztem płacili więcej pracownikom. Jednak ten sposób byłby możliwy tylko w systemie totalitarnym. Społeczeństwa nie godzą się na taki system, ale - ponieważ jednocześnie nie godzą się na pełną gospodarkę rynkową - wybierają coś po środku, czyli tzw. "społeczną gospodarkę rynkową", z którą mamy do czynienia. W związku z tym efekt jest taki, że pracodawcy poszukują sposobów na ograniczenie lub przeniesienie dodatkowych kosztów. Ograniczenie kosztów na pewno nie jest łatwe w praktyce. Pracodawca nie będzie sam się ograniczał tylko dlatego, że jacyś socjalistyczno-populistyczni politycy dobrali się do władzy i mówią mu teraz, ile musi płacić pracownikowi. Dlatego ciężar zrzuci na ludzi: będzie zatrudniał mniej ludzi, ale za to będzie wyciskał z nich wszystkie soki. A że nie wszyscy dają radę, będzie zatrudniał tylko tych, którzy radę dają (czytaj: dają się wykorzystywać). Wyniki badań Neumarka i Waschera [1] potwierdzają hipotezę zastępowania słabo-produktywnych na wysoko-produktywnych pracowników w USA. Autorzy ci tworzą nawet model logit zawierający związki pomiędzy PM, bezrobociem oraz uczeniem się w szkołach. Wykrywają, że wzrost popytu na bardziej produktywnych nastolatków wywołuje taki efekt, że ci nastolatkowie opuszczają szkołę, aby iść do pracy. Następstwem tego jest to, że mniej produktywni nastolatkowie, którzy także opuścili szkołę, nie mają ani pracy, ani szkoły. Niektórzy mogliby powiedzieć, że to nawet dobrze, bo gospodarka powinna się zachowywać zgodnie z teorią Darwina. Równie dobrze można byłoby powiedzieć, że to nawet pozytywne, że jakiś kraj prowadzi wojnę z innym krajem, bo tylko najsilniejsze kraje powinny przetrwać. A jeśli ktoś uważa ten przykład za zbyt skrajny, to weźmy coś podobnego do podatku: to nawet dobrze, że z każdej strony ktoś ludzi okrada, bo tylko najsilniejsi powinni przetrwać. Łatwo zauważyć, że takie rozumowanie prowadzi do patologii. Kłopot polega na tym, że już bez ograniczeń PM przedsiębiorcy będą wybierać tych produktywnych, więc efekt PM tylko sztucznie zwiększa taką presję. Stąd firmy zaczynają wyciskać pracowników jak cytryny. Potem, oczywiście, ludzie (być może ogłupieni przez demagogię i populizm polityków), którzy sami są zwolennikami PM, narzekają na podłość czy chciwość kapitalistów. Po raz kolejny mamy więc do czynienia z krótkowzrocznością lub hipokryzją socjalistów.

Są jednak granice ludzkie i kosztów nie zawsze da się w ten sposób ograniczać, szczególnie gdy następuje, tak jak u nas, co rok podnoszenie PM. Pracodawcy są więc zmuszeni do przeniesienia kosztów na konsumentów, czyli zaczynają podnosić ceny produktów. Nie trzeba być mistrzem w teorii gier, by stwierdzić, że skoro przedsiębiorca wie, że inni przedsiębiorcy są w tej samej sytuacji co on, będą postępować w ten sam sposób, a więc nie staną się bardziej konkurencyjni dla konsumenta, co kształtuje ogólny konsensus, że trzeba podnosić ceny dóbr i usług. W ten sposób rodzi się inflacja. Jest wiele publikacji potwierdzających tę tezę. Aaronson przeprowadził badania na restauracjach w USA i Kanadzie dla okresu 1978-1995 i doszedł do wniosku, że wzrost płacy minimalnej rzeczywiście skutkuje wzrostem ceny za posiłek w restauracjach (w tym fast-foody). Parametry regresji jego modelu zamieściłem poniżej w tabelach.
Dla USA:

 Dla Kanady:

Najważniejsza jest kolumna oznaczona (3), która uwzględnia pełen okres 1978-1995, inflację krajową, bezrobocie, różnice międzyczasowe i regionalne pomiędzy miastami (wiadomo, że zanim zostaną wprowadzone nowe przepisy, musi minąć pewien czas). Autor sprawdził jak się zachowuje inflacja przed i po wdrożeniu nowej PM, dla różnych okresów. W przypadku USA najsilniejszy efekt występuje w oknie 2 miesiące przed i 2 miesiące po tym wydarzeniu, tj. dla okresu (t-2, t+2), gdzie t to miesiąc wprowadzenia nowej PM. Wtedy średnio biorąc wzrost płacy minimalnej o 1% prowadzi do wzrostu inflacji o 0,056%. W przypadku Kanady jest to odpowiednio okno (t-3, t+3) ze średnią elastycznością 0,08%. Gdyby PM urosła o 10%, ceny posiłków za domem wzrosłyby średnio o 0,8% (precyzyjnie byłoby to 0,803% bo model powstaje z logarytmu, więc delogarytmizacja oznacza exp(0,08) = 1,0803).

Pytanie jak wpływałby wzrost PM na całkowitą inflację, a nie tylko tych dóbr, których koszty silnie zależą od PM. Lemos [3] testowała efekt inflacyjny w obliczu wzrostu PM dla Brazylii z lat 1982-2000. Autorka doszła do wniosku, że wzrost PM o 10% powoduje 0,02% wzrostu cen w pierwszym miesiącu nowej stawki, a po dwóch miesiącach o 0,12%. Sumując efekt dostaniemy exp(ln(1,02*1,12)) = 0,1424% wzrostu inflacji w pierwszych 3 miesiącach nowej PM.

Struktura rynków pracy często różni się między krajami, np. w USA stawki PM różnią się w zależności od stanu, natomiast w większości krajów ustanowiona jest tylko jedna uniwersalna stawka. W droższych miastach wzrost PM będzie miał naturalnie słabszy wpływ na ceny. Drugą kwestią są efekty sezonowości (w cenach), które nie zawsze występują w tych samych miesiącach. Są to problemy, które powodują, że model liniowy może nie odzwierciedlać w sposób prawidłowy wpływu zmiany PM na ceny. Dotyczy to np. Francji, dlatego np. Fougere, Gautier i Le Bihan [4] tworzą model nieliniowy, który ma za zadanie poradzić sobie z tymi przeszkodami dla tego kraju z lat 1994-2003. Wnioski z tego modelu są zamieszczone w poniższej tabeli.

Najważniejsza wydaje się tu kolumna oznaczona (1), (2) i (5). W (1) są podane różne poziomy wzrostu PM. W (2) przedstawione są odpowiednie nieliniowe skumulowane po 57 miesiącach skutki (elastyczności) wzrostu PM na ceny dóbr odpowiednio tradycyjnych restauracji i fast-foodów. Kolumna (5) przedstawia długość okresu w miesiącach w jakim utrzymywało się 90% skumulowanego efektu. Średnio 1% wzrostu PM powodował 0,1% skumulowanego wzrostu inflacji po 57 miesiącach. Natomiast 5% wzrostu PM, powodował ok. 0,53% wzrostu cen po tym samym okresie.

Oczywiste jest, że wzrost PM nie prowadzi do identycznego wzrostu inflacji, chociażby z tego powodu, że PM dotyczy tylko pewnego procentu społeczeństwa, podczas gdy inflacja dotyczy wszystkich. Stąd jeżeli PM podnoszona jest o 5%, to nawet te 0,5% większej inflacji po paru latach nie może budzić jakiegoś niepokoju, co więcej po kilku latach psychologia wszystko rozmywa. Dlatego warto spojrzeć na sprawę zmian inflacji w kontekście przed i po wprowadzeniu PM.

Wadsworth [5] testuje nadwyżkową inflację w Wielkiej Brytanii, która wprowadziła PM w kwietniu 1999 r. Poniższa tabela zawiera niektóre parametry wyników, dla okresu od 1997 do 2003.

RPI to retail price index, odpowiednik CPI (consumer price index) lub PPI (producer price index). Wszystkie te idenksy są wskaźnikami stopy inflacji.
NMW to National Minimum Wage.

W wierszu 'Min. wage' i kolumnie 'All NMW goods' mamy wskazaną nadwyżkową roczną inflację w stosunku do ogólnego RPI. W całym okresie roczna inflacja dla dóbr, dla których wprowadzenie PM miało znaczenie (chodzi tu 10 pierwszych sektorów o najwyższym udziale kosztów w PM), była wyższa o 1,12 pkt proc. niż ogólne RPI. W wierszu 'Min. wage x April 1999+' i kolumnie 'All NMW goods' mamy wskazaną nadwyżkową roczną inflację po wprowadzeniu PM w danym okresie, czyli to samo co wcześniej, ale od kwietnia 1999 do końca 2003. W tym przypadku średnioroczna inflacja dla sektorów PM była wyższa o 0,71 pkt proc. w porównaniu do ogólnego RPI. Różnica 1,12 i 0,71 może świadczyć o tym, że przedsiębiorcy dostosowywali ceny do PM jeszcze zanim ta się pojawiła.
Na innej jeszcze tabeli autor porównał inflację z sektorów PM do inflacji z sektorów niezwiązanych z PM i dla okresu po wprowadzeniu PM uzyskał 0,85 pkt proc. rocznej nadwyżki inflacji w sektorach PM.

Podsumowując badania wpływu płacy minimalnej na ceny, powiemy, że już samo wprowadzenie PM zwiększa inflację o ok. 1 pkt proc. (czyli np. z 2% do 3%), natomiast wzrost PM o 10% implikuje wzrost inflacji w restauracjach o ok. 1%. W kontekście giełdy warto też przypomnieć, że empirycznie stwierdzono, że inflacja jest ujemnie skorelowana ze stopami zwrotu z akcji, zob. Czy inflacja jest dobra dla akcji?.

Podsumowując zaś cały artykuł, powiemy, że jego tytuł mógłby się nazywać "Płaca minimalna jako wyciskarka potu i portfeli".


Literatura:
[1] D. Neumark, W. Wascher, Minimum Wage Effects on Employment and School Enrollment, Apr. 1995;
[2] D. Aaronson, Price Pass-through and the Minimum Wage, Feb. 2001
[3] S. Lemos, Empirical Equations to Estimate the Effect of the Minimum Wage on Prices, Iniversity of Leicester, Aug 2004
[4] D. Fougère, E. Gautier, H. Le Bihan, Restaurant Prices and the Minimum Wage, Oct 2010
[5] J. Wadsworth, Did the National Minimum Wage Affect UK Prices?, Mar 2010.

Komentarz do meta-analizy pt. "Why Does the Minimum Wage Have No Discernible Effect on Employment?"

Ten post jest odpowiedzią na komentarz pod poprzednim artykułem:

"Jedną pozycję za płacą minimalną? W stanach mają więcej. Tutaj np. jest omówienie kilku meta badań i nie widać jednoznacznego wpływu na bezrobocie. http://cepr.net/documents/publications/min-wage-2013-02.pdf"
 
Podana przeze mnie literatura odnosi się do wpływu wzrostu minimalnej płacy - w pierwszej części na biedę, czyli bezpośrednie dochody, a w części drugiej - na bezrobocie, czyli pośredni wpływ na biedę. Zalinkowana pozycja Schmitta [1] ( http://cepr.net/documents/publications/min-wage-2013-02.pdf ) odnosi się tylko do części drugiej. Schmitt podaje nawet sam jedno z rozwiązań konfliktu: na skutek wzrostu kosztów płacowych pracodawcy mogą ciąć godziny pracy czy zamrozić dodatkowe świadczenia, a więc liczba pracujących nie spadłaby. Nie widać tu żadnej sprzeczności.

Analizę Schmitta można jednak porównać z pracą Dańskiej-Borsiak. Otóż autorka testowała przyczynowość (test Grangera), tj. efekt zmian minimum pensji na bezrobocie z rocznym opóźnieniem. Nie chodzi tu więc o korelację w tym samym okresie (w meta-analizie Schmitta nie pada nawet słowo Granger). Różnica w opóźnieniu czasowym jest na pewno jedną z przyczyn różnic przeciwstawnych konkluzji.
Jest też wiele innych szczegółów, które należy rozróżnić. Cytując Dańską-Borsiak na temat badań zagranicznych:

"Meer i West [2013] stwierdzili, że zwiększanie płacy minimalnej przyczynia się do zmniejszenia zagregowanego wzrostu zatrudnienia, przy czym zjawisko to nie jest obserwowalne, jeśli analizowany jest poziom zatrudnienia, ale zauważalne, kiedy modeluje się przyrost tej zmiennej. Wynika to z faktu, że zatrudnienie dostosowuje się z opóźnieniem do zwiększonego poziomu płacy minimalnej. Dube [2013] również zauważył negatywną zależność między płacą minimalną a zagregowanym wzrostem zatrudnienia. Jednak dokładniejsza analiza, na poziomie działów, pokazała, że ta zależność jest silnie dostrzegalna w przetwórstwie przemysłowym, która to gałąź zatrudnia stosunkowo niewielką liczbę najniżej opłacanych pracowników a nieistotna w usługach hotelarskich i gastronomicznych, czyli działach zatrudniających łącznie ok. 2/3 takich pracowników. Takie niezgodne z danymi wyniki estymacji świadczą, zdaniem autora, o braku zależności przyczynowej między płacą minimalną a zatrudnieniem ogółem. Błędy te są wynikiem nieuwzględnienia różnic pomiędzy regionami z wysoką i niską wartością płacy minimalnej i momentów jej wzrostu."

Powyższy cytat w dużej mierze wyjaśnia pozorną sprzeczność niektórych badań.
Meta-analiza wydaje się bardzo złym pomysłem w sytuacji, gdy każde badanie używa innej metodologii i mierzy tak naprawdę coś innego (mimo że pozornie to samo). Pogłębioną problematyczność meta-badań opisuje wikipedia:
https://en.wikipedia.org/wiki/Meta-analysis#Problems

W tak skomplikowanej dziedzinie jak ekonomia, metodologia i porównywanie rezultatów musi być wyjątkowo ostrożne. Nie dziwi mnie więc zupełnie, że gdy wszystkie badania zbierzemy do kupy, to skumulowany  efekt wyjdzie na zero.

Dodatkowe kwestie w pracy Dańskiej-Borsiak na temat współczynnika Kaitza (Wsp. Kaitza to stosunek płacy minimalnej do przeciętnej.):
- "Nie stwierdzono zależności przyczynowej między płacą minimalną a liczbą pracujących ogółem ani między płacą minimalną a przyrostem liczby pracujących. Zależność taka nie występuje również między współczynnikiem Kaitza a poziomem i przyrostem liczby pracujących."
- "Obie zmienne: płaca minimalna i współczynnik Kaitza są zaś przyczynami w sensie Grangera dla liczby pracujących w wieku 15-29 lat."
- Chociaż Dańska-Borsiak stwierdza występowanie ujemnej zależności między minimum płacy a liczbą pracujących niezależnie od wsp. Kaitza, to jednak autorka skupia się na niebezpiecznych skutkach dopiero po przekroczeniu 40% wsp. Kaitza. Meta-badania Schmitta tego nie uwzględniają. Może trzeba sprawdzić jak kształtuje się zależność po przekroczeniu pewnego progu? W końcu, jak sądzę, łatwo dowieść, że nie występuje żadna zależność, jeśli wsp. Kaitza byłby na poziomie np. 10%.

I na koniec - Schmitt w dużej mierze skupia się na badaniach Kruegera i Carda. O ich wynikach można dużo dyskutować (zob. wikipedia: https://en.wikipedia.org/wiki/Minimum_wage#Card_and_Krueger), ale zwrócę tylko uwagę, że ich badania dotyczyły jedynie sieci fast-foodów. Po pierwsze godziny pracy są tam bardziej elastyczne. Po drugie rynek fast-foodów jest monopsonistyczny, czyli po prostu jest monopolem na rynku pracodawców. Oznacza to, że ma siłę kreowania płacy poniżej płacy, którą wykreowałby rynek konkurencyjny. W tym więc przypadku minimalna płaca może być poprawnym narzędziem walki z monopolizacją. Tak więc przykład takich monopsonistycznych rynków pracy jest po prostu nieodpowiedni, dlatego że problem płacy minimalnej dotyczy całego rynku pracy. Gdyby płaca minimalna dotyczyła tylko monopsonów, to byłaby zupełnie inna dyskusja. Gdyby rzeczywiście dowiedziono realne sterowanie płacami przez takie firmy, to wtedy ekonomiści nie spieraliby się raczej ze sobą, a co najwyżej etycy.


Literatura:
[1] J. Schmitt, Why Does the Minimum Wage Have No Discernible Effect on Employment?, Feb. 2013, link: http://cepr.net/publications/reports/why-does-the-minimum-wage-have-no-discernible-effect-on-employment
[2] B. Dańska-Borsiak, Płaca Minimalna A Liczba Młodych Pracujących. Związki Przyczynowe I Prognozy Wariantowe, Uniwersytet Łódzki, 2014, link: http://cejsh.icm.edu.pl/cejsh/element/bwmeta1.element.desklight-4feddeec-395b-4ec8-9f3b-aada3ae4e2fd

Rząd podnosi wynagrodzenie minimalne do 2000 zł brutto - oznacza to wzrost bezrobocia w 2018

Nasz dobry rząd ma podnieść wynagrodzenie minimalne od stycznia 2017 r. o 8,1% w stos. do 2016, czyli do 2000 zł brutto. Bo przecież najłatwiej kazać innym podnieść koszty. Co więcej, E. Rafalska komentuje:
 - Dzięki temu zmniejszy się różnica między wynagrodzeniem średnim, a minimalnym. Zbliżymy się do pożądanych 50 proc. Dobra sytuacja na rynku pracy powinna przekładać się także na wzrost wynagrodzeń.

Reszta na stronie: http://www.regiopraca.pl/portal/rynek-pracy/wiadomosci/placa-minimalna-2017-2000-zlotych-od-pierwszego-stycznia

Dobrze, że dodano komentarz dr Małgorzaty Starczewskiej-Krzysztoszek, głównej ekonomistki Konfederacji Lewiatan:

"Tak wysoki wzrost płacy minimalnej z 1850 zł do 2000 zł może być bardzo niekorzystny dla mikrofirm, które są zwykle mniej efektywne, a średnie wynagrodzenie w nich niewiele przekracza 50 proc. płacy w dużych firmach, a jednocześnie jest tylko trochę wyższe niż płaca minimalna. Dla 96 proc. mikrofirm wysoka podwyżka płacy minimalnej będzie problemem i skłoni przynajmniej część z nich do przejścia do szarej strefy."

Na http://demotywatory.pl/4589316/WIG-20-a-PIS pojawił się swego czasu taki obrazek:
 

Choć od tego czasu giełda się poprawiła, to nadal jest poniżej punktu, od którego PIS przejął władzę.

Wzrost pensji minimalnej najprawdopodobniej spowoduje, że giełda polska będzie spadać jeszcze co najmniej przez 2 lata. Dlaczego tyle? Nie chodzi tu o kolejne wybory parlamentarne, ale właśnie o wynagrodzenie minimalne. Nieco rozświetlę ten temat.

Bardzo przyjemne (bo krótkie) podsumowanie poglądów o płacy minimalnej w ekonomii przedłożył Szarfenberg [1] w 2014 r. Zaczyna od motta:

„... płaca minimalna jest przede wszystkim sprawą polityczną, a koncentrowanie uwagi na modelach ekonomicznych, jakby to one miały kierować procesem politycznym jest całkowicie chybione” Oren M. Levin-Waldman

Nie wiem kto to jest Levin-Waldman, choć google stwierdza, że to spec od ekonomii politycznej. Może i coś w tym jest.

Szarfenberg podaje cały szereg argumentów zwolenników jak i przeciwników płacy minimalnej. Nie będę tu ich przytaczał, bo artykuł Szarfenberga jest dostępny w internecie (link podałem w przypisach).
Ogólnie można powiedzieć, że obrońcy płacy minimalnej albo nie rozumieją jak funkcjonują mechanizmy rynkowe (i w ogóle świat) albo wydaje im się, że wszyscy pracodawcy żyją w zmowie, maksymalizując zyski poprzez maksymalne obniżanie kosztów, czyli wynagrodzeń. Zatem pracodawcy nie konkurują między sobą jak to mówi pre-klasyczna ekonomia, tylko się wzajemnie wspierają. Idąc tym tropem, można byłoby rozszerzyć tę spiskową teorię i powiedzieć, że na rynku jest tylko jeden pracodawca - i oczywiście nie-Polak, tylko Żyd albo Niemiec.

Jasne - są duże sieci monopolistyczne, które rzeczywiście wykorzystują swoją siłę i na przykład dzięki tzw. korzyściom skali ceny ich produktów są niższe niż w sklepach detalicznych, które niewątpliwie na tym cierpią. Ale jakoś obrońcy wynagrodzenia minimalnego nie mają z tym problemu. W końcu im niższa cena tym lepiej! Czysta hipokryzja albo po prostu krótkowzroczność.

A jeżeli nawet pracodawcy nie są w zmowie, to - według socjalistycznych orędowników płacy minimalnej - ludzie są za słabi by sami wymagać godziwego wynagrodzenia, dlatego państwo ma ich za to wyręczać. Jakie to przyjemne - nowi na rynku pracy podczas rozmowy kwalifikacyjnej nie muszą się głowić nad własną wartością rynkową, bo państwo już ich wyceniło.

Szarfenberg waży te dwa przeciwstawne stanowiska, przywołując przykładowe badania statystyczne - będące głosami zarówno za jak i przeciw. Do tego drugiego nurtu zaliczymy wnioski S. Borkowskiej [6]:

„Ogólnie rzecz biorąc, wzrost płacy minimalnej najsilniej oddziałuje na spadek zatrudnienia młodzieży (do 24 roku życia), a w szczególności młodocianych (do 18–19 roku życia)”

Szarfenberg chcąc zachować obiektywizm wskazuje na jedną pozycję w literaturze ekonomicznej, w której autorka pozytywnie ocenia wpływ płacy minimalnej. Cytuje tutaj C. Saget [2]:

„Analiza danych daje silne wsparcie twierdzeniu, że płaca minimalna może mieć pozytywne rezultaty w łagodzeniu ubóstwa poprzez poprawę warunków życia pracowników i ich rodzin, nie mając negatywnego wpływu na zatrudnienie”

Zajrzałem do tej pracy. Saget bada jedynie kraje rozwijające się z Afryki, Ameryki Łacińskiej i Azji. Te z Azji, jakby ktoś pytał, to: Azerbejdżan, Turcja, Filipiny, Tajlandia i Syria. Nie wiem jak inni, ale dla mnie wszelkie dane dot. aktywności ekonomicznej z tych krajów powinny być traktowane z założenia jako podejrzane. Ale nawet pomijając te podejrzenia jedna rzecz dyskwalifikuje ten artykuł. W wersji, która jest darmowa w internecie (i jak sądzę aktualna) autorka pokazuje tabelę z wynikami relacji między biedą a minimalnym wynagrodzeniem:

Częściowy komentarz Saget do tej tabeli:

"The relationship between the minimum wage and poverty remains when the level of development, as approximated by GDP/capita and location are introduced as explanatory variables.5 This can be seen from the bottom of Table 5 (second column), which relates the share of population in poverty to GDP per capita in dollars GDPCAP, minimum wage in dollars MINWDOL, average wage in
dollars AWAGEDOL and four regional dummies."

Zaznaczyłem pogrubioną czcionką "four", bo Saget odnosi się tu do 4 regionów: Afryki Północnej, Afryki Południowej, Ameryki Łacińskiej i Azji. Są to zmienne sztuczne w modelu regresji, tzw. dummy variables albo dummies, które przybierają wartość 0 (fałsz) lub 1 (prawda), wskazując tym samym istotność wpływu danego regionu. Jednak w rzeczonej dolnej części tablicy są tylko 3 z tych regionów, tak jakby 4-ta gdzieś się zgubiła (brakuje Azji). W dodatku analiza zawiera bardzo małą liczbę obserwacji. To wszystko sprawia, że analizy Saget nie można brać na poważnie.

Ludzie przeczytają takie prace niezbyt dokładnie, a potem się nimi posługują jako argumentami na poparcie swojej tezy. Problem naszych czasów polega na tym, że od dziecka ludzie uczeni są, że każdy może wypowiadać się w kwestii ekonomii tak samo jak polityki. Ekonomię traktuje się prawie na równi z polityką. Mamy przecież "ekonomię polityczną". Tak więc premier czy inny polityk nie wie o czym mówi, a ludzie tego słuchają. Ale nie chodzi tylko o polityków, ale też samych ekonomistów. Są różne poziomy ekonomistów. Nie mając przygotowania ani wiedzy, ludzie nie odróżnią eksperta od pseudo-eksperta. Dobrym przykładem jest następujące ćwiczenie: wpisałem w google frazę "wplyw placy minimalnej w polsce". Na drugim miejscu pojawił się artykuł Wielki mit płacy minimalnej. Jej podniesienie nie zwiększa bezrobocia. Czytanie tego to strata czasu, ale przytoczę jeden fragment:

"– Amerykanie potrafili dostrzec pozytywny wpływ racjonalnej polityki płacowej na rozwój gospodarczy. Henry Ford już w 1914 r. wprowadził w swojej firmie minimalną płacę dzienną w wysokości 5 dol. Była to wysoka kwota, bo np. samochód, który wówczas był towarem luksusowym, kosztował 450 dol. Początkowo wszyscy twierdzili, że Ford zbankrutuje, ale dzięki temu wyraźnie wzrosła wydajność pracy w firmie."

Szok, żenada, jak to nazwać? Nie wiem czy cytowany "profesor" czy po prostu autor tego artykułu nie rozumie czym jest płaca minimalna. Gdyby przedsiębiorca mógł sam ustalać wynagrodzenie dla swojego pracownika, to zaprzeczałoby to właśnie idei płacy minimalnej, którą socjalistyczny autor próbuje nam narzucić. Takie artykuły, które pojawiają się nie tylko na pierwszych stronach, ale na pierwszych miejscach wyszukiwarki, stanowią właśnie przyczynę zacofania społeczeństwa w zakresie wiedzy ekonomicznej.

Co w takim razie mówią poważni ekonomiści na zadany temat? Analizując to zagadnienie dla USA, Sabia i Burkhauser w 2010 [3] stwierdzają, że "stanowe i federalne minimalne płace zwiększane pomiędzy 2003 a 2007 nie miały żadnego wpływu na poziom stopy biedy". Dodatkowo również zanotowali negatywny wpływ spadku zatrudnienia. Ich konkluzja brzmi:

"Nasze wyniki sugerują, że wzrost minimalnej płacy stanowi nieodpowiedni sposób do pomocy ubogim pracującym".

Przyglądając się innym badaniom ci sami autorzy zdradzają:

"Ostatnio przeprowadzano wiele badań na temat wpływu wzrostu minimum płacy na dochody i biedę (zob. np. Card i Krueger 1995; Addison i Blackburn 1999; Neumark i Wascher 2002; Gundersen i Ziliak 2004; Neumark, Schewitzer i Wascher 2004, 2005; Burkhauser i Sabia 2007; Sabia 2008) i wszystkie poza jedną zauważały, że podwyżki minimalnych płac nie miały w przeszłości żadnego efektu."

Tym wyjątkiem był artykuł Addisona i Blackburna z 1999 [4]. Przejrzałem go. Mimo że faktycznie ogólne rezultaty przemawiały za ujemną korelacją pomiędzy wzrostem minimalnego wynagrodzenia a stopą biedy, to gdy bliżej się im przyjrzymy, przestają być już tak oczywiste. Najbardziej uderzające jest to, że gdy autorzy podzielili badanie na 2 okresy 1983-1989 oraz 1989-1996, to tylko w drugim okresie minimalne wynagrodzenie miało istotny statystycznie wpływ. Cały efekt wynikał więc z drugiego okresu. Trochę pachnie przypadkiem.

Wszystkie powyższe artykuły skupiały się na szukaniu związku między zmianami min. płacy a poziomem biedy, najczęściej liczonej w dochodach rodziny. Prostszym sposobem jest zmierzenie po prostu poziomu bezrobocia wśród młodych grup zawodowych, których głównie dotyczy ta kwestia. Artykułów zagranicznych o tym jest cała masa. Można też znaleźć artykuły dotyczące Polski; np. jest artykuł B. Dańskiej-Borsiak z 2014 r. , dostępny w internecie [5]. Autorka dochodzi do następującego wniosku:

"Wykazano, że zarówno poziom płacy minimalnej, jak i jej stosunek do wynagrodzenia przeciętnego są przyczynami w sensie Grangera liczby pracujących w wieku 15-29 lat w Polsce w okresie 1990-2013. Stwierdzono również, ceteris paribus, negatywny wpływ obu wymienionych zmiennych na liczbę młodych pracujących, przy czym w przypadku płacy minimalnej ten efekt jest opóźniony o jeden rok. Prognozy wariantowe do roku 2020 wskazują największą liczbę pracujących, jeśli płaca minimalna nie przekroczy 40% wynagrodzenia przeciętnego przy jednoczesnym utrzymaniu obecnego tempa wzrostu płacy minimalnej."

Ostatnie dane GUS wskazują, że przeciętne wynagrodzenie brutto wyniosło w 2 kw. 2016 ponad 4000 zł. Oznacza to, że minimalna płaca obecnie jest za wysoka i nie powinna przekroczyć 1600 zł brutto.

Równie ważne jest ostatnie zdanie w cytowanej wyżej pracy:

"Uzyskane rezultaty mogą stanowić głos w powracającej co roku dyskusji na temat podnoszenia płacy minimalnej. Postulowane przez związki zawodowe ustalenie jej na poziomie 50% wynagrodzenia przeciętnego wydaje się bardzo niekorzystne z punktu widzenia poziomu zatrudnienia."

Od 2017 będziemy mieć już poziom 50%. Od 2018 r. należy się więc spodziewać wzrostu bezrobocia. Ktoś mógłby spytać, że skoro obecnie min płaca > 40% przeciętnej płacy, to dlaczego bezrobocie jest obecnie tak niskie? Tylko że jej skok nastąpił w 2009 r., a potem ją jeszcze w latach 2012-2013 podnoszono:

 Źródło: wikipedia. Link: https://pl.wikipedia.org/wiki/P%C5%82aca_minimalna#/media/File:Minimalne_wynagrodzenie_jako_odsetek_przecietnego_wynagrodzenia_w_gospodarce_narodowej.png

Po roku 2013 też nastąpił wzrost stosunku minimalnej do przeciętnej płacy, ale spowolnił. Wg założeń PIS wzrost ten znów przyspieszy od 2017.

Dla porównania bezrobocie wśród młodych:

Źródło: http://rynekpracy.org/x/946883


Znając giełdę dyskontującą PKB (które jest ujemnie skorelowane z bezrobociem), spadki zaczną się wcześniej.




Literatura:

[1] R. Szarfenberg, Kontrowersje wokół podniesienia płacy minimalnej, Instytut Polityki Społecznej Uniwersytet Warszawski, 2014, link: rszarf.ips.uw.edu.pl/pdf/placmin.pdf

[2] C. Saget, Is the Minimum Wage an Effective Tool to Promote Decent Work and Reduce Poverty? The Experience of Selected Developing Countries, International Labour Office, 2001, link: http://www.ilo.org/employment/Whatwedo/Publications/WCMS_142310/lang--en/index.htm

[3]  J. J. Sabia, R. Burkhauser, Minimum Wages and Poverty: Will a $9.50 Federal Minimum Wage Really Help theWorking Poor?, Jan. 2010;

[4] J. T. Addison, M. L. Blackburn, Minimum Wages and Poverty, Apr. 1999;

[5] B. Dańska-Borsiak, Płaca Minimalna A Liczba Młodych Pracujących. Związki Przyczynowe I Prognozy Wariantowe, Uniwersytet Łódzki, 2014, link: http://cejsh.icm.edu.pl/cejsh/element/bwmeta1.element.desklight-4feddeec-395b-4ec8-9f3b-aada3ae4e2fd

[6] S. Borkowska, Minimum Wages and Reducing Poverty, University of Łódź, 2001, link1:  http://unpan1.un.org/intradoc/groups/public/documents/nispacee/unpan004913.pdf , link2: http://unpan1.un.org/intradoc/groups/public/documents/nispacee/unpan004779.pdf

"Metody najmniejszych kwadratów i niektóre alternatywy" - książka Hartera

Chyba najlepszym sposobem na zwiększenie pokory wobec nauki jest zobaczenie jak ogromny postęp dokonał się w danej dziedzinie w określonym przedziale czasu. Na przykład w ekonometrii osobną poddziedziną można nazwać metodę najmniejszych kwadratów (MNK), której historia zaczyna się mniej więcej od XVIII w. (choć pre-historia od Galileusza, od 1632 r.). Harter opisał ją bardzo, bardzo szczegółowo w książce "The Method of Least Squares and Some Alternatives". Wersję z 1972 r. można pobrać w słabej jakości z poniższego linku:

www.dtic.mil/dtic/tr/fulltext/u2/752211.pdf

Dowiadujemy się, że przed narodzinami MNK narodziła się metoda najmniejszych błędów absolutnych opisana przez Boscovicha w 1757, a także metoda największej wiarygodności, którą zaproponował Bernoulli w 1778. Mimo iż MNK kojarzy się dziś tylko z funkcją regresji, a więc ze zmienną warunkową, jej historia zaczęła się od pytania o właściwe określenie średniej dla zmiennej niewarunkowej. Duży wkład w tym temacie miał Laplace, który w 1781 najpierw przedstawił 4 kryteria, którymi można się kierować przy wyborze miary centralnej tendencji:
1) można wymagać takiej średniej, aby suma dodatnich błędów równała się sumie ujemnych błędów (średnia arytmetyczna);
2) można wymagać, aby suma dodatnich błędów przemnożonych przez ich odpowiednie prawdopodobieństwa równała się sumie ujemnych błędów przemnożonych przez ich odpowiednie prawdopodobieństwa (średnia ważona);
3) można wymagać, aby średnia była najbardziej prawdopodobną prawdziwą wartością (kryterium największej wiarygodności Bernoulliego);
4) można wymagać, aby błąd był minimalny; tzn. aby suma iloczynów błędów i ich prawdopodobieństw była najmniejsza.

Laplace pokazał, że kryterium (4), które uważał za podstawowe, jest równoważne kryterium (2). Pokazał też, że (4) prowadzi do średniej arytmetycznej i w ten sposób zgadza się z (1) pod warunkiem, że:
1. rozkład prawdopodobieństwa jest taki sam dla wszystkich obserwacji;
2. rozkład jest symetryczny;
3. błąd może dążyć do nieskończoności, ale wtedy jego prawdopodobieństwo dąży do zera.

Później w 1805 r. Legendre jako pierwszy opublikował MNK. Gauss również jej używał, jeszcze przed swoimi publikacjami. W 1809 r. Gauss publikuje twierdzenie, że w symetrycznym i jednomodalnym (czyli z jedną dominantą) rozkładzie istnieje tylko jedno prawo - tzw. normalne prawo błędów - dla którego najbardziej prawdopodobną wartością jest średnia arytmetyczna. Prawdopodobieństwo odchylenia jest proporcjonalne do exp(-h x^2), gdzie h = 1/(2s^2), s - odch standardowe, x - zmienna losowa będąca odchyleniem (błędem) od wartości oczekiwanej. Zatem Gauss powiązał kryterium (1) z (3) Laplace'a (pamiętajmy, że mówimy tu ciągle jeszcze o zmiennej niewarunkowej). Jednocześnie dowiódł, że MNK, którą zaprezentował Legendre, stanowi konsekwencję prawa błędów. W 1810 Laplace dowiódł, że przy ogólnych warunkach rozkład średnich w próbie dąży do normalnego. W 1816 r. Gauss zauważył, że nie jest potrzebna precyzja h, aby zastosować MNK. Prawo błędów dostarcza informacji o prawdopodobieństwie odchylenia od średniej, natomiast MNK dostarcza średnią wartość estymatora. W 1818 Laplace porównał MNK z metodą najmniejszych błędów absolutnych zaproponowaną przez Boscovicha i doszedł wniosku, że pierwsza z nich prowadzi do średniej arytmetycznej, natomiast druga do mediany. W końcu w 1823 Gauss uzasadnił użycie MNK bez założenia normalności rozkładu odchyleń.

W 1830 r. Hauber rozszerzył  pracę Gaussa na estymację, gdy obserwacje pochodzą z (możliwie) różnych populacji - o różnych wariancjach, a więc zmienna x przestaje być IID.

W ten sposób rozpoczęła się era teoretycznych odkryć MNK wraz z jego alternatywami. Im dalej, tym modele coraz bardziej złożone, ale i dokładniejsze. Dziś Uogólniona MNK, nieliniowa MNK czy nawet nieparametryczne MNK stały się standardem w specjalistycznych programach do ekonometrii.

Darmowa wersja z 1972 r. kończy się na roku 1972. Harter napisał drugą wersję w 1974. Mimo iż różnica to tylko 2 lata, Autor dodał i opisał dodatkowo jeszcze 118 pozycji. Większość z nich ma zastosowanie do modeli ekonomicznych i finansowych. Myślę, że dzisiaj byłoby to dziesiątki tysięcy.

Średnia warunkowa czy niewarunkowa?

Finansiści, stosując od czasu do czasu regresję liniową, np. model trendu, rzadko myślą o zmiennej losowej warunkowej. Ale to właśnie pojęcie warunkowości tworzy różnicę pomiędzy zwykłą średnią arytmetyczną a stopą w modelu trendu. Ostatnio pokazałem to za pomocą "Smarującego estymatora" (SE) Duana. SE posłużył mi jako oczekiwana stopa zwrotu w dwóch przypadkach:
1) gdy cena rośnie wykładniczo w czasie, tzn. prawdziwy jest model P(t) = e^(bt + składnik losowy), przy czym składnik losowy może pochodzić z dowolnego rozkładu;
2) gdy cena nie zależy od czasu, tzn. średnio znajduje się ciągle na tym samym poziomie. Np. WIG od końca 10.2006 do końca 10.2016 to praktycznie linia płaska:

Okazało się, że w tym drugim przypadku SE sprowadza się do niewarunkowej średniej arytmetycznej stopy zwrotu. Natomiast gdy istnieje wykładnicza zależność od czasu, to SE jest warunkową średnią równą e^b*D, gdzie D to korekta Duana liczona jako średnia arytmetyczna z wykładniczych składników losowych e^(składnik losowy). Zatem, jeżeli czas staje się warunkiem dla zmian kapitału, to średnia niewarunkowa przekształca się w średnią warunkową.

Jednak inwestor przyzwyczajony do pojęcia stopy zwrotu zaczyna się zastanawiać: w jaki sposób czas miałby w ogóle wpływać na stopę zwrotu? Przecież po to właśnie jest pojęcie stopy, czyli procentu, aby uniezależnić zmiany kapitału od kolejnych okresów. Ale gdy spojrzymy na to zagadnienie tak jak na różnicę pomiędzy średnią arytmetyczną a geometryczną, odpowiedź staje się jaśniejsza: gdy obliczamy średnią geometryczną, uwzględniamy fakt, że wartość kapitału zależy od okresu poprzedniego, bo jest jakby oprocentowany. Natomiast gdy wyznaczamy średnią arytmetyczną, każdą zmianę kapitału traktujemy całkowicie niezależnie od poprzednich okresów. To stąd przecież powstaje różnica pomiędzy "długookresową średnią stopą zwrotu" a "krótkookresową średnią stopą zwrotu", wskazując w pierwszym przypadku na czasową zależność zmian kapitału oraz w drugim przypadku na ich niezależność.

A stąd już tylko krok do zrozumienia różnicy pomiędzy warunkową a niewarunkową średnią: ta pierwsza zawiera część stochastyczną D oraz część systematyczną e^b. Część systematyczna jest niczym innym jak średnią geometryczną brutto w rozkładzie ciągłym. Oczywiście jest różnica między rozkładem ciągłym a dyskretnym, ale w modelu ciągłym zakładamy, że pomiędzy dwoma oddalonymi punktami możemy wstawić pewną średnią z tych punktów, ponieważ czas jest ciągły. Nie będzie to średnia arytmetyczna, ale właśnie geometryczna. Jeżeli mamy okres pomiędzy 10 a 11, np. 10,5 i chcemy wyznaczyć teoretycznie ten punkt, to zauważmy, że średnia geometryczna brutto z wartości pomiędzy okresem 10 a 11 równa się (e^10*e^11)^0,5 = e^(21*0,5) = e^10,5. Trzeba jednak zaznaczyć, że przejście od rozkładu dyskretnego do ciągłego w rzeczywistości wszystko zmienia, bo o ile w dyskretnym stopy brutto wewnątrz okresu się redukują, tak że wpływ na średnią ma jedynie pierwsza i ostatnia wartość, o tyle w ciągłym już tego zrobić nie mogą i jest to poniekąd przyczyna, dla której średnia geometryczna brutto w rozkładzie ciągłym staje się równa medianie, co odpowiada temu co napisałem kiedyś w Istota i znaczenie logarytmicznej stopy zwrotu.

Oczywiście trzeba pamiętać, że średnia warunkowa jest znacznie szerszym pojęciem niż tylko w kontekście czasu. Częściej średnia warunkowa traktowana jest w powiązaniu z inną zmienną losową. Np. w dwuwymiarowym rozkładzie normalnym, w którym zmienne losowe X i Y są ze sobą skorelowane, wartość oczekiwana Y pod warunkiem, że X = x jest dana wzorem [2]:

Jeżeli współczynnik korelacji ρ jest równy zero, warunkowa wartość oczekiwana Y sprowadza się do niewarunkowej wartości oczekiwanej m(Y). W przeciwnym razie Y zależy od zachowania X. Na przykład Y może być stopą zwrotu z akcji, a X stopą zwrotu z indeksu giełdowego. Gdyby obie pochodziły z rozkładu normalnego, to przedstawiona relacja byłaby zawsze prawdziwa i zawsze liniowa. Widać więc, jak istotną rolę pełni warunkowość, którą można rozpatrywać zarówno w kontekście przestrzeni jak i czasu.

Literatura:
[1] N. Duan, Smearing Estimate: A Nonparametric Retransformation Method, Sep. 1983,
[2] Z. Hellwig, Elementy rachunku prawdopodobieństwa i statystyki matematycznej, PWN W-wa 1998.