Po drugie parametry modelu, jak i ogólny model muszą być istotne statystycznie.
Po trzecie model musi być stabilny - parametry modelu nie mogą się zmieniać w czasie.
Po czwarte muszą być spełnione odpowiednie warunki rozkładu prawdopodobieństwa składnika losowego. Po piąte trzeba sprawdzić liniowość / nieliniowość modelu. Ten ostatni warunek pomijam, natomiast czwarty zostanie wspomniany.
Należy rozróżniać stacjonarność i stabilność.
Stacjonarność rozumiana jest jako niezmienność rozkładu prawdopodobieństwa w czasie, a co najmniej niezmienność średniej danego procesu w czasie.
Z kolei stabilność oznacza stałość parametrów regresji. Np. jeśli mamy model AR(1):
x(t) = b*x(t-1) + e,
gdzie x(t) to np. stopa zwrotu w okresie t, zaś e to składnik losowy,
to warunkowa wartość oczekiwana zmiennej x(t) jest równa b*x(t-1). Jednakże wyznaczenie parametru b może być sztuczne, jeśli kształt regresji ulega zmianom w czasie. Dlatego musimy mieć pewność, że parametr b będzie stabilny. Powstaje pytanie jak sprawdzić czy parametry modelu pozostają stabilne w czasie? Najbardziej znane są 3 testy na stabilność modelu:
1. Test Chowa
2. Test CUSUM
3. QLR
Ad1) Test Chowa
W 1960 r. ekonomista G. Chow opracował test sprawdzający czy parametry regresji z dwóch różnych próbek są takie same. Najczęściej w ekonomii podejście to służy do testowania czy występuje punkt zwrotny w danym procesie. Cały okres dzielony jest wtedy na dwie podpróby, a moment czasowy rozdzielający je nazywamy punktem zwrotnym. To podejście jest stosowane w Gretlu.
Spróbujemy zrobić przykłady. Zanim jednak zaczniemy, dopowiedzmy, że Gretl automatycznie dzieli daną próbę na połowę, aby porównywać dwa różne okresy. Jest to podejście w miarę poprawne, jednak z praktycznego punktu widzenia lepszym rozwiązaniem wydaje się najpierw na oko oszacować czy w analizowanym okresie mają miejsce istotne zmiany kierunku. Np. możemy starać podzielić na okres hossy i bessy.
W artykule Czy oczekiwane stopy zwrotu w ogóle się zmieniają? analizowałem mWIG40 dla różnych częstości, aby sprawdzić hipotezę stacjonarności. Hipoteza ta dla wszystkich częstości została potwierdzona przez testy ADF i KPSS. Te same dane wykorzystamy teraz do sprawdzenia stabilności modelu. Zaczniemy od miesięcznych stóp zwrotu mWIG40 od początku notowań styczeń 1998-pażdziernik 2014; 198 obserwacji. Poniżej jest wykres notowań mWIG40:
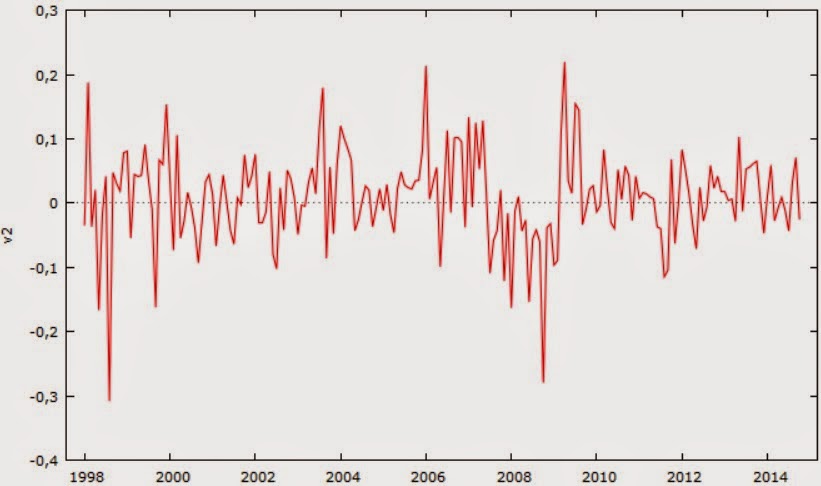
Stopy zwrotu:
Ustalimy hipotetyczny punkt zwrotny w czerwcu 2007 r., gdzie miesięcznie zanotowany został szczyt historyczny. Aby dokonać testu, musimy najpierw wejść w Gretlu w Model -> Klasyczna Metoda Najmniejszych Kwadratów. Tutaj stworzymy klasyczną autoregresję. Pytanie jednak brzmi jakiego rzędu? AR(1), AR(2), a może więcej? Z pomocą przychodzi metodologia Boxa-Jenkinsa, zgodnie z którą teoretyczny model AR(p) ma funkcję autokorelacji cząstkowych (PACF) równą zeru dla opóźnień większych od p (tzn. współczynniki autokorelacji cząstkowej dla opóźnień większych niż p są nieistotne) [1].
Dotychczas nigdy nie wspomniałem o PACF, a jedynie o ACF. Czytelnik, który czytał Czy oczekiwane stopy zwrotu w ogóle się zmieniają? , zapamiętał, że zwróciłem uwagę na to, iż ACF nie pokazuje tak naprawdę autokorelacji, jeśli proces jest niestacjonarny. Jest on właśnie przydatny do naocznego oszacowania czy mamy do czynienia z procesem stacjonarnym poprzez analizę współczynników autokorelacji kolejnych rzędów. Jeżeli są one istotnie dodatnie i spadają z każdym opóźnieniem powoli, to znaczy, że prawdopodobnie mamy proces niestacjonarny (aczkolwiek w artykule Ułamkowa stacjonarność? Co to za twór? wykazałem, że metoda ta może przynieść błędne rezultaty). Z czego to wynika? ACF zawiera wewnętrzne zależności pomiędzy wartościami pośrednimi, np. autokorelacja 5 rzędu, tj. ACF(5) zawierać będzie nie tylko autokorelację pomiędzy obserwacją piątą a bieżącą, ale także autokorelacje pomiędzy obserwacjami pośrednimi, czyli np. 1, 2, 3 i 4 rzędu. Dopiero tzw. cząstkowa autokorelacja, tj. PACF, usuwa te pośrednie zależności., tak że dostaniemy poprawniejszą formę autokorelacji danego rzędu. Przy tym jednak pamiętać trzeba, że PACF jest równa ACF dla 1 rzędu, więc dla procesów niestacjonarnych również ona ma ograniczoną stosowalność. Box i Jenkins doszli do wniosku, że o ile ACF może służyć do oceny stacjonarności procesu (a przez to także determinować właściwy rząd średniej kroczącej w modelu MA), o tyle PACF może służyć za czynnik determinujący rząd w modelu AR.
Oto porównanie ACF(p) i PACF(p) dla miesięcznych zamknięć (czyli nie stóp zwrotu!) mWIG40:
Nie trzeba nawet sprawdzać autokorelacji stóp zwrotu, aby ocenić, że do modelowania AR(p) wystarczy p = 1.
W Gretlu wybierając KMNK, musimy wybrać zmienną zależną, którą jest tu stopa zwrotu. Regresorem będzie stopa zwrotu z opóźnieniem 1. Nie wstawiamy żadnej zmiennej jako regresor, bo poniżej jest opcja "opóźnienia", gdzie wybieramy opóźnienia dla zmiennej zależnej od 1 do 1. Dodatkowo zaznaczamy opcję "Odporne błędy standardowe". Głównym zadaniem regresji odpornej jest umożliwienie uzyskania oszacowań niepodatnych na obserwacje odstające [2]. Jak wiadomo KMNK, która wymaga normalności i homoskedastyczności składnika losowego, nie jest prawidłową metodą dla giełdowych zmian ze względu na występowanie w ich rozkładzie grubych ogonów (rzadkie zdarzenia, które są częstsze niż w rozkładzie normalnym), heteroskedastyczności i efektów ARCH. Pomiędzy tymi 3 cechami nie ma ścisłej zależności, istnieje jednak pewien związek. Modele ARCH można tak skonstruować, by pojawiły się w nich grube ogony [3], [4]. Niestety nie ma możliwości zrobienia testu stabilności przy modelowaniu GARCH, który jest oddzielną funkcją w Gretlu. Dlatego używamy regresji odpornej. Statystyka odpornościowa używa zamiast średniej np. mediany lub obciętej średniej.
Po wybraniu odpowiednich opcji otrzymałem nieistotną stałą i istotny parametr autoregresji 0,164.
1 gwiazdka oznacza istotność na poziomie 10%, dwie gwiazdki oznaczają istotność na poziomie 5%, 3 gwiazdki na poziomie 1%. W tym przypadku mamy 5% istotności, czyli pewności, że hipoteza o nieistotności parametru jest prawdziwa - jest to na tyle mało, że ją odrzucamy.
Oprócz sprawdzania istotności poszczególnych parametrów, należy też ocenić całościową istotność modelu, czyli de facto współczynnika determinacji R^2. Taki test wykonuje Statystyka F (test F-Snedecora). Widać, że wartość p dla testu F = 0,018692, zatem jest to znów poniżej 5%. Jednak to co jest uderzające, to niezwykle niska wartość R^2, która jest mniejsza od 0,03. Praktyczna zmienność stóp zwrotu w porównaniu do modelowanej stopy zwrotu staje się więc zbyt duża do praktycznego wykorzystania. Jednakże naszym celem nie jest ocena faktycznej przydatności AR, a jedynie zbadanie stabilności modelu.
Wchodzimy Testy -> Test zmian strukturalnych Chowa. Oto wyniki:
Ad 2) Test CUSUM
W wielu sytuacjach niedogodnością testu Chowa jest to, że trzeba wskazywać w nim hipotetyczny punkt zwrotny. CUSUM (Cumulated Sum of Residuals) zwany czasami (nie do końca poprawnie) testem Harveya-Colliera) weryfikuje hipotezę o stabilności modelu bez potrzeby wskazywania punktu zwrotnego. Został on zaproponowany przez Browna, Durbina i Evansa w 1975 r. Wchodzimy w Testy -> test stabilności CUSUM. Dostajemy wyniki w formie tekstowej i graficznej.
Jeżeli wykres nie przekracza wartości progowych, czyli niebieskich linii to znaczy, że model można uznać za stabilny. Jak widać tak się nie dzieje, a więc model pozostaje stabilny. Dodatkowo CUSUM wskazał poziom p = 0,99 > 0,05, czyli brak istotności. Parametr ten jednak jest niezbyt przydatny, co się okaże później.
Zatem CUSUM dał przeciwstawne wyniki w stosunku do Chowa.
Trzeba jednak zaznaczyć, że CUSUM opiera się na założeniu, że zmiany strukturalne modelu mają charakter deterministyczny. Odmianą testu CUSUM jest CUSUMQ (Cumulated Sum of Squares Residuals), który może być bardziej niż CUSUM przydatny w sytuacji gdy zmiany struktury modelu mają charakter całkowicie przypadkowy (ze względu na to, że bierze kwadraty różnic to jest bardziej wrażliwy na progi istotności). Wybieramy Testy -> test stabilności CUSUMQ. Dostajemy wyniki w graficznej formie:
W tym przypadku również patrzymy czy wykres przecina niebieską linię. Trzeba przyznać, że wyniki są zupełnie nieoczekiwane. Test sugeruje, że parametry lekko zmieniły się w 2000 r. - to jest w czasach bessy oraz w 2009-2011 r., czyli w czasach niedawnej hossy. Rok 2007 i 2008 były dla testu całkowicie "normalne" pomimo gwałtownych wzrostów i spadków.
Ad 3) Test QLR
Jeśli nie wiemy kiedy nastąpi załamanie strukturalne modelu, ale spodziewamy się, że kiedyś nastąpi, wtedy możemy użyć testu QLR (Quandt Likelihood Ratio). Test ten powstał jako pierwszy ze wszystkich 3 testów, w pracy Quandta w 1958 i 1960 r. W przeciwieństwie do CUSUM zakłada on, że zmiany strukturalne mają charakter stochastyczny [5]. Wybieramy Testy -> test stabilności QLR. Otrzymujemy wyniki:
Bardzo niska wartość p wskazuje na załamanie strukturalne, które wystąpić miało w lipcu 2000 r. Wprawdzie test QLR działa prawidłowo wtedy, gdy daty punktów krytycznych są stosunkowo odległe od punktów daty początku i końca, lecz w tym przypadku rok 2000 nie jest zupełnie na początku, a ponadto data pokrywa się z tym co przedstawia test CUSUMQ.
Przeprowadzimy teraz krótką analizę AR(1) tygodniowych stóp zwrotu mWIG40 w okresie styczeń 2006:październik 2014. Tym razem Przetestujemy tylko CUSUM. Ogólna charakterystyka podana jest poniżej
Parametr autoregresji jest bardzo istotny (na poziomie 1%) i równa się 0,22 (tyle samo wynosi autokorelacja).
Pomimo że wartość p = 0,32 dla CUSUM, a więc wskazuje na nieistotność, to tak naprawdę nie decyduje o tym, czy model miał czy nie miał załamania. Należy spojrzeć na wykres czy nastąpiło przecięcie linii.
Tym razem wg CUSUM struktura modelu zmieniła się dosłownie od marca 2009 r., czyli od początku hossy. Ciekawe, że tym razem zmiana została uznana za deterministyczną, czyli tak jakby pewna zewnętrzna cecha wpłynęła na model. Dodatkowo spójrzmy na CUSUMQ
Test wskazuje na zmianę parametrów już w 2008 r. i niestabilność ta trwała aż do 2013 r. Dopiero od 2013 r. model się "ustabilizował". W przeciwieństwie do CUSUM, CUSUMQ dostarcza informacji o przypadkowej niestabilności modelu w okresach dla miejsc poza niebieską linią.
Powyższa analiza tygodniowych stóp zwrotu manifestuje "wewnętrzne sprzeczności" i trudności w ocenie ekonometrycznej. Stacjonarność danych, wysoka autokorelacja i istotność statystyczna parametrów stoją w sprzeczności do testów Chowa, QLR, CUSUM, CUSUMQ, które często odrzucają stabilność modelu.
Literatura:
[1] E. M. Syczewska, Wprowadzenie do modeli ARMA/ARIMA, W-wa 2011,
[2] D. Korniluk, Metody regresji odpornej, Prezentacja w ramach spotkan zespołu przygotowujacego sie do Econometric Game 2014, 2014
[3] B. O. Bradley and Murad S. Taqqu, Financial Risk and Heavy Tails, 2001
[4] D. Politis, A Heavy-Tailed Distribution for ARCH Residuals, 2004
[5] Discussion Of The Paper By Dr Brown, Professor Durbin And Mr Evans (jako dodatek do artykułu Browna, Durbina i Evansa "Techniques for Testing the Constancy of Regression Relationships over Time", 1975).