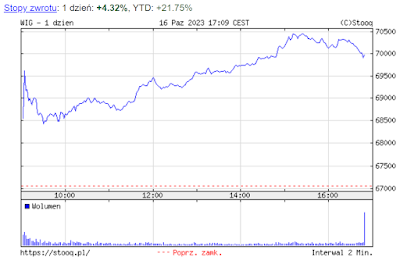
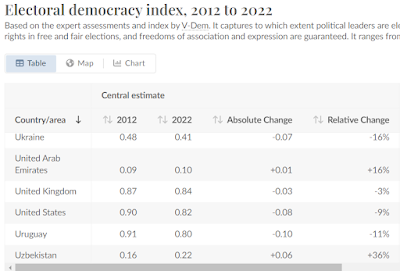
W ostatnich kilku miesiącach sWIG80 rozjeżdża się z WIG20:
Indeks małych spółek znajduje się wręcz w trendzie spadającym, natomiast WIG20 osiąga nowe szczyty. Ta dywergencja jest na tyle silna, że warto wykorzystać ją do postawienia pytania, czy małe spółki zapowiadają bessę, ewentualnie "trend" horyzontalny. sWIG80 często traktuje się jak termometr prognozy gospodarczej, ponieważ małe spółki lepiej odzwierciedlają stan całej gospodarki niż duże.
Naukowo zostało to dowiedzione np. w badaniu E. Widz [1], z którego wynika, że chociaż zarówno duże, średnie, jak i małe spółki korelują wyprzedzająco ze zmianami PKB, to wpływ PKB na giełdę występuje jedynie dla sWIG80. Nawiasem mówiąc autor raczej błędnie interpretuje swoje wyniki, ponieważ stwierdza, że indeksy giełdowe są przyczyną zmian PKB. Pisałem już o tym
tutaj, że przyczynowość w sensie Grangera jest po prostu nazwą na wyprzedzenie w korelacji: inwestorzy po prostu dyskontują cząstkowe informacje przychodzące wcześniej niż oficjalne dane PKB. Pieniądze nie biorą się z nieba, a co najwyżej można starać się dowieść, że zwiększony dług publiczny zwiększa PKB i zainwestowanie środków w akcje jest czymś analogicznym. Jednak ludzie nie zaciągają kredytów i pożyczek, żeby nakupować akcji. W każdym razie jedyną istotną informacją w badaniu Widz jest właśnie ten kierunek odwrotny, tzn. od PKB do giełdy. A to okazuje się jedynie dotyczyć sWIG80 właśnie.
Czyli opadający sWIG80 informuje o słabnącej gospodarce. To jednak nie oznacza jeszcze, że maluchy można traktować jako prognostyk nadchodzącej bessy - bo dawałoby to możliwość przewidywania. Gdyby każdy tak przewidywał, to reakcja dużych spółek musiałaby natychmiast dostosować się do małych: gdyby każdy wiedział, że za parę miesięcy duże spółki zaczną spadać, to każdy będzie grał co najwyżej na krótki termin. Powiedzmy, że średni inwestor postanowi sprzedać akcje za miesiąc. Ale przecież wie, że inni też tak zrobią. To znaczy, że nie będzie w stanie sprzedać po odpowiedniej cenie. Wobec tego skróci termin. Ale wie, że inni też skrócą. Za dwa-trzy tygodnie nikt od niego nie będzie odkupował. Wobec tego skróci do tygodnia. Ale wie, że inni pomyśleli to samo, że muszą skrócić, więc też skrócą. Chociaż się wydaje to tylko teorią, to czysta logika ekonomiczna prowadzi do wniosku, że właściwie, to może jedynie uprawiać daytrading pod warunkiem, że występują duże wahania. Generalnie będzie to jednak oznaczało spadek popytu w kolejnych dniach, ponieważ nie każdy trader będzie w stanie (lub nie będzie chciał) tak działać i dlatego trend powinien rzeczywiście się dostosować do spadkowego.
Teoria efektywnego rynku będzie działać pod dwoma warunkami. Większość inwestorów musi być racjonalna (czyli przeprowadzać powyższy tok rozumowania) oraz musi być ich wystarczająco wielu. Dlaczego to drugie jest tak ważne? Nie chodzi tu wbrew pozorom o płynność, ale to, że jeśli inwestorów będzie za mało, to powstaje ryzyko, że założą koalicję i zaczną sztucznie nakręcać kurs, żeby potem sprzedać paru naiwniakom.
Do czego doszliśmy? Załóżmy, że są spełnione te dwa założenia. W takiej sytuacji sWIG80 nie może być prognostykiem WIG20. Ale to nie oznacza jeszcze, że WIG20 będzie się dostosowywał do sWIG80. Inwestorzy wcale nie muszą brać pod uwagę sWIG80, jeśli uznają, że nie ma on wpływu na wycenę akcji dużych spółek. To znaczy, jeżeli gospodarka Polski znajdzie się w recesji, to nie znaczy automatycznie, że duże spółki też znajdą się w recesji. Powiedzmy np., że rząd wprowadza duży podatek dla małych przedsiębiorstw, a duże mogą go uniknąć. Weźmy lepszy przykład. Poprzednio pisałem, że WIG silnie urósł po wyborach, ponieważ inwestorzy wierzą, że spada ryzyko polityczne. Ale przecież to ryzyko dotyczy bardziej dużych spółek niż małych, ponieważ Skarb Państwa ma udziały tylko w dużych spółkach. Warto też odnotować ostatnie badanie przeprowadzone przez KPMG, z którego wynika, że niepewność polityczna dotyczy właśnie dużych firm (zob.
raport). Widzimy więc, że dywergencja między dużymi a małymi spółkami ma logiczne podstawy.
W sumie ostatni miesiąc traktowałbym jako zdarzenie jednorazowe. Z tej perspektywy kierunek nadal byłby spadkowy lub horyzontalny, gdyby tylko sWIG80 wyznaczył kierunek na przyszłość.
Sprawdźmy więc czy rzeczywiście indeks małych spółek wyprzedzał duże w przeszłości.
Oto wykresy dla logarytmów z obu indeksów w tygodniowych interwałach:
Test wykonałem w R przy pomocy funkcji
lowess (ang.
locally weighted scatterplot smoothing - lokalnie ważone wygładzanie wykresów), a także wykorzystałem kod, który
ktoś zamieścił na StackOverflow na znajdowanie lokalnego ekstremum. Dla maksimów dostałem taki obraz:
Czerwona pionowa linia wskazuje max sWIG80, niebieska pionowa linia - WIG20.
I tak:
- pierwszy max sWIG wyprzedzał
- drugi max WIG20 wyprzedzał
- trzeci max oba indeksy w tym momencie wskazały
- czwarty max sWIG80 pierwszy
- piąty niejasna sytuacja, była dywergencja, prawdopodobnie spowodowana zniknięciem OFE
- szósty oba tak samo
- siódmy sWIG80 szybszy
- ósmy oba w tym samym momencie
Teraz to samo dla minimów:
W tym wypadku nie ma sensu nawet wyliczać dołki, bo niemal wszędzie się nakładają czerwone z niebieskimi.
Widzimy, że wcale nie można polegać na małych spółkach jako kierunkowskazie.
Literatura:
[1] Widz, E., Wahania koniunktury giełdowej a wahania koniunktury gospodarczej w Polsce–analiza przyczynowości w sensie Grangera. Prace Naukowe Uniwersytetu Ekonomicznego We Wrocławiu, nr 531, 2018.
Dodatek:
Kod w R:
#pakiet xts dla wygody
if (require("xts")==FALSE) {
install.packages("xts")
library("xts")
}
# ścieżki i ładowanie danych ....
# mamy indeksy: cena1, cena2 oraz daty: daty1, daty2, WIG20 od 1991 r., sWIG80 od 1995 r.
cena1_xts = xts(cena1, order.by=daty1)
cena2_xts = xts(cena2, order.by=daty2)
# scalanie szeregów czasowych tylko dla dopasowanych dat, czyli od 1995
ceny_xts <- merge(cena1_xts, cena2_xts, join="inner")
ceny_mat <- as.matrix(ceny_xts)
# logarytm indeksu
logcena1 = log(x=ceny_xts[,1])
logcena2 = log(x=ceny_xts[,2])
# filtr lowess
filtr1 = lowess(logcena1, f=0.01)$y
filtr2 = lowess(logcena2, f=0.01)$y
# zamieniam na zwykły wektor, bo potem są problemy z wykresem
logcena1 = as.numeric(logcena1)
logcena2 = as.numeric(logcena2)
# funkcja Evan'a Friedlanda (https://stackoverflow.com/questions/6836409/finding-local-maxima-and-minima)
inflect <- function(x, threshold){
up <- sapply(1:threshold, function(n) c(x[-(seq(n))], rep(NA, n)))
down <- sapply(-1:-threshold, function(n) c(rep(NA,abs(n)), x[-seq(length(x), length(x) - abs(n) + 1)]))
a <- cbind(x,up,down)
list(minima = which(apply(a, 1, min) == a[,1]), maxima = which(apply(a, 1, max) == a[,1]))
}
linieEkstremum <- function(filtrn, is_plot_new, maks) {
# w tym przypadku to nie ma istotnego znaczenia jakie n, dotyczyło wielkości ekstremów dla punktów
n <- 2
# ustawiłem dla min 50, dla max 60, bo dało to lepszy efekt wizualny, ale to można sobie zmieniać dowolnie. Większe powoduje usunięcie mniejszych ekstremów, tzn. lokalność ekstremum rośnie w kierunku globalności
bottoms <- lapply(1:n, function(th) inflect(filtrn, threshold = 50)$minima)
tops <- lapply(1:n, function(th) inflect(filtrn, threshold = 60)$maxima)
if (is_plot_new==TRUE) {
plot(x=index(filtrn), y=filtrn, type = 'l', ylim=c(min(filtr1, filtr2), max(filtr1, filtr2)),
col="darkred", main="", xlab="", xaxt="n")
datyWykres = seq(from=daty1[1], to=daty1[length(daty1)], length.out=round(length(daty1)/96))
indeksWykres = seq(from=1, to=length(filtrn), length.out=round(length(filtrn)/96))
axis(side=1, cex.lab=1, cex.axis=0.8, at=indeksWykres, las=2, labels=format(datyWykres,"%Y-%m"), hadj=1)
mtext(text="okres", side=1, adj=0.5, padj=5.2)
for(i in n:n){
if (maks==1) {
abline(v=tops[[i]], col="red")
} else if (maks==0) {
abline(v=bottoms[[i]], col="red")
}
}
} else {
lines(index(filtrn), filtrn, type = 'l', col="darkblue")
for(i in n:n){
if (maks==1) {
abline(v=tops[[i]], col="blue")
} else if (maks==0) {
abline(v=bottoms[[i]], col="blue")
}
}
}
}
# tylko log-cena
linieEkstremum(logcena1, is_plot_new=TRUE, maks=-1)
linieEkstremum(logcena2, is_plot_new=FALSE, maks=-1)
legend("topleft", legend=c("sWIG80", "WIG20"), col=c("darkred", "darkblue"), lty = 1, lwd = 2)
# filtr + maksima
linieEkstremum(filtr1, is_plot_new=TRUE, maks=1)
linieEkstremum(filtr2, is_plot_new=FALSE, maks=1)
legend("topleft", legend=c("sWIG80", "WIG20"), col=c("darkred", "darkblue"), lty = 1, lwd = 2)
# filtr + minima
linieEkstremum(filtr1, is_plot_new=TRUE, maks=0)
linieEkstremum(filtr2, is_plot_new=FALSE, maks=0)
legend("topleft", legend=c("sWIG80", "WIG20"), col=c("darkred", "darkblue"), lty = 1, lwd = 2)