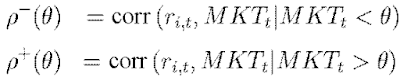Są to dane objęte okresem styczeń 1970-grudzień 1993. W nawiasach kwadratowych podano korelacje bez wyjątkowego października 1987. Przykładowo między rynkiem USA a Niemiec całkowita korelacja wyniosła 0,348. Ale gdy obydwa rynki rosły, korelacja (Up-Up) wyniosła zaledwie 0,086, natomiast gdy oba rynki spadały (Down-Down), korelacja podniosła się do 0,52 (a bez 10.1987 - 0,41).
Powyższe badanie traktowało rynki na równi, co ma znaczenie dla zbudowania odpowiednio zdywersyfikowanego portfela. Bo załóżmy, że mamy możliwość zainwestowania w jakieś kraje. Zamiast brać do analizy całkowitą korelację, moglibyśmy wziąć korelację Down-Down. Wtedy budowa portfela Markowitza wyglądałaby tak samo jak klasyczna, ale zamiast zwykłych średnich stóp zwrotu, użylibyśmy stopy zwrotu Down-Down (tj. ujemnych stóp zwrotu, które odpowiadałyby tym korelacjom) oraz odchylenie standardowe Down-Down. Zauważmy, że w takim podejściu minimalizowalibyśmy nie tylko ryzyko w sensie semiwariancji (Down-Down), ale także wartość bezwzględną z oczekiwanej stopy zwrotu, która byłaby przecież ujemna. Chociaż musiałbym to sam dokładnie sprawdzić, to wydaje mi się, że analiza portfela stałaby się praktyczniejsza, bo nie musielibyśmy wybierać oczekiwanej stopy zwrotu portfela, ale szukalibyśmy największej możliwej, czyli blisko zera. Ale to na inny temat.
Powiedzmy, że w uproszczeniu analizujemy samą korelację, zakładając, że inne zmienne są takie same dla różnych krajów. Na przykład zastanawiamy się czy zainwestować w USA i Niemcy czy też w USA i Francję. Całkowita korelacja jest mniejsza dla pary USA-Niemcy, więc wydaje się ona lepszym wyborem. Ale przecież tylko dla okresu Down-Down niższa korelacja jest korzystniejsza, a już dla Up-Up jest na odwrót (bo mówimy o pozycji długiej). Gdy przyjrzymy się podziałowi korelacji, zauważymy, że para USA-Francja ma większą korelację w okresie Up-Up (0,266) oraz mniejszą w okresie Down-Down (0,483) w porównaniu do USA-Niemcy. Czyli para USA-Francja stałaby się portfelem efektywnym, a para USA-Niemcy nieefektywnym, odwrotnie niż początkowo stwierdziliśmy.
Dla inwestora aktywnego, poszukującego najlepszych inwestycji, ważniejsze od precyzyjnej dywersyfikacji staje się porównanie jego portfela (akcji) z indeksem giełdowym. W takiej sytuacji jego portfel nie będzie traktowany na równi z indeksem / portfelem rynkowym. Trzeba założyć, że aktywa będą podlegały rynkowi w jakimś stopniu. Pytanie brzmi w jakim stopniu? Aby znaleźć odpowiedź, musimy zbadać korelację tego aktywa z indeksem pod warunkiem, że indeks rośnie albo spada. Innymi słowy mamy tu pojedynczą korelację-Up i korelację-Down. Korelację-Down będę nazywał korelacją dolnostronną, a korelację-Up korelacją górnostronną. Najczęściej to korelacja dolnostronna stanowi czynnik ryzyka.
Ang et al. [2] zdefiniowali obydwa rodzaje korelacji następująco:
gdzie pierwsza z minusem to korelacja-Down i druga z plusem to korelacja-Up. Stopa r(i, t) to stopa zwrotu z i-tego aktywa. MKT(t) - market, czyli stopa zwrotu z portfela rynkowego albo indeksu giełdowego. Stopa MKT ma korelować z r(i, t) pod warunkiem, że jest mniejsza (większa) od pewnej wartości, która dla nas będzie równa zero.
Obliczmy całkowitą, dolnostronną i górnostronną korelację dla polskiego rynku. (W Excelu można to zrobić na dwa sposoby. Pierwszy to zapisać w dwóch kolumnach odpowiednio funkcje, wykorzystując funkcję Jeżeli stopa zwrotu z indeksu mniejsza od 0, to odpowiednia stopa zwrotu, w przeciwnym wypadku pusty znak. Z tego wyznaczamy współczynnik korelacji. Drugi sposób to formuła tablicowa).
Test: miesięczne stopy zwrotu w okresie luty 2000 - luty 2018:
1. WIG jako zwykły portfel akcji vs. S&P500 jako portfel rynkowy (MKT):
a) całkowita korelacja = 0,62
b) korelacja-down = 0,6.
c) korelacja-up = 0,28
Jak widać w miesiącach rosnących WIG zachowywał się "słabiej", a w spadkowych mocno korelował z indeksem USA.
Następnie sprawdziłem kilka spółek na tle WIG (jako MKT):.
2. KGHM vs. WIG
a) całkowita korelacja = 0,7
b) korelacja-down = 0,47.
c) korelacja-up = 0,55
3. Amica vs. WIG:
a) całkowita korelacja = 0,5
b) korelacja-down = 0,51
c) korelacja-up = 0,3
4. Budimex vs. WIG:
a) całkowita korelacja = 0,41
b) korelacja-down = 0,33
c) korelacja-up = 0,35
5. Stalexport vs. WIG:
a) całkowita korelacja = 0,38
b) korelacja-down = 0,4
c) korelacja-up = 0,17
6. Lubawa vs. WIG:
a) całkowita korelacja = 0,4
b) korelacja-down = 0,12
c) korelacja-up = 0,31
7. Elzab vs. WIG:
a) całkowita korelacja = 0,37
b) korelacja-down = 0,29
c) korelacja-up = 0,2
Ta pobieżna analiza wskazuje, że spadkom WIGu nie zawsze towarzyszyła większa korelacja z poszczególnymi akcjami, w przypadku Lubawy i KGHM rosnący rynek im sprzyjał. Dodatkowo LBW wydaje się być odporna na spadki rynkowe.
Jednak powyższa analiza to bardzo długi okres czasu. Korelacja może się przecież zmieniać w czasie. Wykonałem te same obliczenia, ale tym razem od 2010 r.
II) Test: miesięczne stopy zwrotu w okresie styczeń 2010 - luty 2018:
1. WIG jako zwykły portfel akcji vs. S&P500 (jako MKT):
a) całkowita korelacja = 0,6
b) korelacja-down = 0,5
c) korelacja-up = 0,47
Całkowita korelacja między WIG a indeksem USA pozostała stabilna, ale dolnostronna nieco spadła, a górnostronna znacznie wzrosła.
2. KGHM vs. WIG
a) całkowita korelacja = 0,66
b) korelacja-down = 0,46
c) korelacja-up = 0,4
3. Amica vs. WIG:
a) całkowita korelacja = 0,38
b) korelacja-down = 0,39
c) korelacja-up = 0,19
4. Budimex vs. WIG:
a) całkowita korelacja = 0,39
b) korelacja-down = 0,09
c) korelacja-up = 0,31
5. Stalexport vs. WIG:
a) całkowita korelacja = 0,29
b) korelacja-down = -0,06
c) korelacja-up = 0,32
6. Lubawa vs. WIG:
a) całkowita korelacja = 0,46
b) korelacja-down = 0,31
c) korelacja-up = 0,2
7. Elzab vs. WIG:
a) całkowita korelacja = 0,33
b) korelacja-down = 0,23
c) korelacja-up = 0,14
Nasuwają się tutaj 2 wnioski. Po pierwsze struktura zmieniła się, tak, że 4 z 6 spółek posiadają teraz większą korelację-down niż korelację-up. Po drugie, zastanawiające są statystyki STX i BDX. Korelacja-down dla STX odwróciła się niemal o 180 stopni, spadając z 0,4 do -0,06, co w istocie znaczy brak korelacji z WIG w okresach spadków. W dodatku korelacja-up znacząco wzrosła. Sugeruje to, że te akcje można trzymać w większym udziale niż inne. Natomiast w przypadku BDX korelacja-up prawie się nie zmieniła, natomiast bardzo spadła korelacja-down. Gdy WIG spadał, BDX prawie nie reagował. Innymi słowy, niezależnie od kierunku indeksu, był to dobry okres dla tej spółki.
Niestety problem, jak widać, polega na tym, że korelacja zmienia się w czasie, co zresztą wykrywały już liczne badania zagraniczne [1, 2, 3, 4, 5] i nie możemy mieć pewności co do tego samego poziomu korelacji w przyszłości. Możemy jednak posłużyć się nowoczesnymi, dynamicznymi modelami, jak np. modelem Engle'a [3], które prognozują ten poziom.
Literatura:
[1] Erb, C. B., Harvey, C. R., Viskanta, T. E., Forecasting International Equity Correlations, Dec. 1994;
[2] Ang, A., Chen, J., Xing, Y., Downside Correlation and Expected Stock Returns, Mar 2002;
[3] Engle, R. F., Shephard, K., Theoretical and Empirical properties of Dynamic Conditional Correlation Multivariate GARCH, Dec 2001;
[4] Wong, A. S. K., Vlaar, P. J. G., Modelling time-varying correlations of financial markets, Sep 2003;
[5] Solnik, B., Boucrelle, C., Fur, Y. L., International Market Correlation and Volatility, Sep. - Oct., 1996.
