Jak powstają cykle i podcykle? Część szósta i ostatnia.

Dlaczego w ogóle mówię o chaosie? Przecież miało być o cyklach giełdowych!
To pytanie można byłoby też odwrócić: Jak to może być, że trajektorie chaotyczne charakteryzują się cyklicznością? Przecież chaos wyklucza porządek, tj. cykliczność!

Jeśli chodzi o pierwsze pytanie, to warto podkreślić, że nowoczesna teoria cykliczności uległa w ostatnich dziesięcioleciach drastycznej przemianie.
"Coraz lepiej zdajemy sobie sprawę z tego, że w świecie zjawisk zachodzących wokół nas, na wielu poziomach budowy materii i w rozmaitych skalach czasu, przebiegają procesy porządkowania i niszczenia porządku. Na razie wiedza o tych procesach jest niepełna i mało dokładna, dlatego w tej dziedzinie wiele jest jeszcze do zbadania i naukowcy będą przez wiele lat mieli co robić. Jednak już teraz wiemy, że Wszechświat na pewno nie jest podobny do kartezjańskiego zegara, w którym czas płynie jednostajnie i może być traktowany jako absolutny zewnętrzny parametr, porządkujący stany w istocie podobne do siebie. Poszukując metafory bardziej odpowiedniej i bogatszej powiedziałbym raczej [to znaczy nie ja, tylko autor cytatu], że Wszechświat bardziej niż zegar przypomina skomplikowaną symfonię, której melodię poznaliśmy dotąd bardzo wyrywkowo." [M. Tempczyk, Skale czasu układów dynamicznych, Zagadnienia Filozoficzne w Nauce, XXVIII-XXIX / 2001, s. 8].

W niedawnym czasie wiedza naukowców o o długookresowym działaniu naszego układu planetarnego znacznie się poszerzyła się. "W roku 1988 G.J. Sussman i J. Wisdom z MIT stosując komputery zbadali ruch planet w okresach czasu rzędu setek milionów lat i wykazali, że ruch Plutona jest chaotyczny z czasem charakterystycznym rzędu pięćdziesięciu milionów lat. Rok później J. Laskar z Bureau des longitudes zbadał dynamikę Układu Słonecznego w okresie dwustu milionów lat i wykazał, że ruch planet najbliższych Słońca, w tym także Ziemi, jest chaotyczny z okresem rzędu dziesięciu milionów lat. Laskar odkrył także, że ruch Wenus jest chaotyczny w stopniu umożliwiającym zmianę kierunku obrotu tej planety wokół osi. Ponieważ obecnie kręci się ona przeciwnie do ruchu obrotowego pozostałych planet, istnieje uzasadnione podejrzenie, że w ciągu swego istnienia zmieniała ona kilka razy kierunek obrotu."[M. Tempczyk, ibidem, s. 7].

Jak widzimy omawianie cykliczności w kontekście chaosu nie dotyczy tylko cykli giełdowych. Można byłoby powiedzieć, że sam czynnik ludzki - świadomość - potrafi zaburzyć nie tylko okresowość na rynkach, ale nawet cykle biologiczne i klimatyczne. Ale świadomość to po prostu pewna zmienna, którą można byłoby potraktować jako czynnik wymuszający chaos. Zmiennych może być jednak wiele i jak się okazuje mają one wpływ (choć dopiero po długim okresie czasu) na coś, co wydawałoby się całkowicie stabilne i tak ważne dla nas - ruch Ziemi. Jeśli więc ruch Ziemi jest chaotyczny, to czy można o nim mówić jako o periodycznym? Można, ale należy mieć na uwadze, że jest to ruch w przybliżeniu okresowy. Cykle giełdowe będą również istnieć - jednak w sposób ułamkowy.

Jeśli chodzi o drugie pytanie, to już częściowo na nie odpowiedziałem powyżej. Można powiedzieć, że cykle chaotyczne są "ułamkowe". Oznacza to, że są niestabilne - po pewnym czasie przestają istnieć, stają się "bardziej chaotyczne". Jednak istnienie niestabilnych orbit okresowych w nieliniowych układach dynamicznych jest faktem matematycznym. Dowód został przedstawiony na przykład w pracy doktorskiej Zbigniewa Galiasa, Analiza i przetwarzanie sygnałów chaotycznych, Kraków 1995).

Przede wszystkim należy wiedzieć, że typowa trajektoria odwiedza wszystkie części atraktora i przechodzi nieskończenie wiele
razy dowolnie blisko każdego punktu należącego do atraktora. [Z. Galias, Analiza i przetwarzanie sygnałów chaotycznych, Kraków 1995, s. 19].

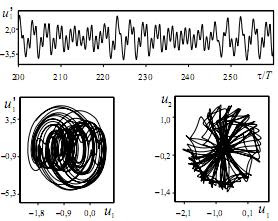
Jeśli więc znajdziemy trajektorię, która będzie przynajmniej kilka razy pod rząd, w tym samym czasie (czyli zgodnie z jakimś okresem) powracać bardzo blisko punktu startu, to możemy przyjąć, że jest to ruch okresowy. Nie jest to więc ruch stricte okresowy, czyli taki, że punkt końcowy-powrotny idealnie łączy się z punktem startu. Można by powiedzieć, że mamy tu ruch quasi-okresowy (prawie okresowy). Ruch quasi-okresowy jest czymś pomiędzy ruchem całkowicie okresowym a chaotycznym. Quasi-okresowa orbita różni się tym od chaotycznej, że jeśli znamy na nią wzór, to w każdym momencie możemy przewidzieć jej położenie i nie ma czegoś takiego jak wrażliwość na warunki początkowe. Quasi-okresowa orbita jest specyficznym złożeniem orbit okresowych. Przykładem jest f = cos(2^(1/2)*x) + cos(x). Na dole mamy wykres tej funkcji.



Jeśli otoczenie danego punktu trajektorii będzie wystarczająco małe i odległość pomiędzy dwiema quasi-okresowymi trajektoriami będzie mniejsza od średnicy tego otoczenia, to możemy spokojnie przyjąć, że te dwie trajektorie odpowiadają tej samej trajektorii okresowej. Jeśli dysponujemy nieskończenie długim ciągiem próbek pochodzących z trajektorii odwiedzającej wszystkie części atraktora to zmniejszając średnicę otoczenia będziemy znajdować coraz więcej orbit okresowych zanurzonych w dziwnym atraktorze. W praktyce jednak dysponujemy ciągiem skończonym. Wybierając zbyt małe otoczenie nie wykryjemy istnienia orbit okresowych, zwłaszcza tych, które leżą w rzadziej odwiedzanych częściach atraktora. Wybór zbyt dużej wartości średnicy otoczenia spowoduje, że nie znajdziemy wielu z dłuższych orbit okresowych, które leżą blisko orbit krótszych. [Op. cit. Z. Galias, ibidem, s. 26].

Poniżej przedstawiono przykład znalezionej orbity okresowej w układzie Lorenza (wynika z twierdzenia Pilarczyka, 2000).



Poniżej przedstawiono przykład wybranych orbit okresowych odwzorowania Henona (rys. z Z. Galias, ibidem, 29). Są to tylko punkty - jest to bowiem odwzorowanie dyskretne.



Okazuje się, że najłatwiej odkrywać orbity okresowe za pomocą odwzorowań Poincarego - na mapach Poincarego. Wtedy bowiem skupiamy się jedynie na punktach przecięcia trajektorii z pewną płaszczyzną. Jeśli obserwujemy, że punkty powrotne po określonym czasie znajdują się w małym dozwolonym otoczeniu, otrzymujemy orbitę okresową.

Mapa Poincarego pozwala także lepiej zrozumieć fraktalność atraktora chaotycznego. Ponieważ każda trajektoria przechodzi nieskończenie wiele razy dowolnie blisko każdego punktu należącego do atraktora, mapa będzie bardzo "zwartym" obiektem. A jednak, jeśli obiekt ten leży na płaszczyźnie, to ze względu na brak ciągłości pomiędzy punktami, nie będzie on posiadał dwóch wymiarów, choć intuicyjnie powinien. Na przykład atraktor Henona, który wcześniej przedstawiałem, posiada wymiar fraktalny (ułamkowy) wynoszący ok. 1,28. Pomimo, że trajektoria chaotyczna może być ruchem całkowicie ciągłym, to już ze względu na to, że mapa Poincarego posiada wymiar ułamkowy, atraktor chaotyczny zanurzony w trójwymiarowej przestrzeni fazowej, nie będzie posiadał wymiaru rzędu 3, ale pomiędzy 2 a 3 (jeśli bowiem byłby trójwymiarowy, obraz płaszczyzny rozcinającej go w pewnym miejscu powinien mieć dokładnie dwa wymiary). Na przykład atraktor Lorenza posiada wymiar fraktalny ok. 2,06 (tak mało, bo te jego listki są prawie dwuwymiarowe). Jeśli rozpatrujemy rynki kapitałowe, to prawdopodobnie pierwszym, który odkrył istnienie atraktorów chaotycznych jest E. E. Peters, który w książce "Teoria chaosu a rynki kapitałowe" opisuje swoje wyniki i tak: dla S&P 500 wymiar fraktalny wynosi 2,33. Dla MSCI Niemcy 2,41, dla SCI Wielka Brytania 2,94 oraz dla MSCI Japonia 3,05. Oznacza to, że dla trzech pierwszych rynków ruch trajektorii można modelować za pomocą trzech zmiennych, a ostatni japoński rynek za pomocą czterech zmiennych.

Przypomnę, że przedstawiony na tym blogu model składa się z trzech zmiennych: nastroju (chciwość, strach), niezdecydowania (niepewności) oraz czynnika fundamentalnego ("przyspieszenia" lub "opóźnienia" kapitału). Zauważmy, że całą przestrzeń fazową tworzą ogólnie dwa czynniki: psychologiczny i fundamentalny, przy czym pierwszy dzieli się na nieracjonalny (ograniczenie racjonalny) i racjonalny.

Wynika z tego, że nasz model można przystosować do faktycznej rynkowej trajektorii (z wyjątkiem rynku japońskiego), gdyż atraktor o mniej niż trzech wymiarach można zanurzyć w przestrzeni fazowej o trzech zmiennych.

Fraktalność atraktora można w pewnym sensie przełożyć na fraktalność szeregu czasowego pewnej zmiennej trajektorii. O ile fraktalność atraktora jest przestrzenna, o tyle fraktalność szeregu czasowego jest czasowa. Z punktu widzenia realizacji procesu stochastycznego, rozkład prawdopodobieństwa jest w każdej skali czasowej taki sam. Jednostki czasu możemy przecież dowolnie dobierać - i to właśnie stąd wynika. Jeśli więc wyobrazimy sobie atraktor miesięcznej stopy zwrotu, to teoretycznie atraktor tygodniowej stopy zwrotu powinien być identyczny. Wykresy dzienne i tygodniowe cen akcji powinny być nieodróżnialne od miesięcznych. Rzeczywistość okazuje się jednak bardziej skomplikowana - dla dziennych i tygodniowych stóp zwrotu wykresy są dużo bardziej poszarpane i nieprzewidywalne niż dla miesięcznych stóp zwrotu (Por. Peters, ibidem, s. 113). Realny proces na giełdach nie jest więc w pełni samopodobny. Z czego to wynika? Dodatnia korelacja pomiędzy dziennymi stopami zwrotu jest mniejsza niż korelacja pomiędzy tygodniowymi stopami zwrotu, a ta jeszcze mniejsza niż pomiędzy miesięcznymi stopami zwrotu. Widocznie dzienne stopy zwrotu mają większą skłonność do powrotów do średniej. Z czasem jednak korelacja pomiędzy miesięcznymi zwrotami stabilizuje się, tak że jedno, kilku-, kilkunasto- i kilkudziesięciomiesięczne wykresy stają się statystycznie nierozróżnialne. W końcu, po wielu miesiącach, korelacja (pamięć rynku) zaczyna spadać do zera.

Doszliśmy wreszcie do końcowego praktycznego wniosku. Wykrywanie orbit okresowych w układach chaotycznych umożliwia tzw. stabilizację orbit, czyli sterowanie układów chaotycznych. Skoro można znaleźć trajektorię okresową o co najmniej kilku zmiennych, to tym bardziej można znaleźć trajektorię o jednej zmiennej, tzn. okresowy szereg czasowy. Jeśli tę zmienną stanowi stopa zwrotu, to znaleźliśmy swego rodzaju cykl giełdowy. Dzienna stopa zwrotu będzie zawierać większy szum i nie znajdziemy widocznej okresowości. Jednak coraz większe "otoczenie czasowe" pozwoli wykryć coraz lepiej dodatnio (nieliniowo) skorelowane stopy zwrotu.

Można powiedzieć, że Peters wykrył takie "orbity okresowe". Badał on różne rynki kapitałowe, biorąc za okres 1 miesiąc. Jego wyniki są następujące: w USA tracimy zdolność do prognozowania po ok. 4 latach (48 miesięcy), dla Wielkiej Brytanii pamięć rynku wynosi 36 miesięcy, a Japonii 44 miesiące. Z kolei z analiz N. Siemieniuka w pracy "Fraktalne właściwości polskiego rynku kapitałowego" wynika, że polski rynek kapitałowy tracił pamięć po 218 tygodniach, czyli 55 miesiącach. Ze względu na mniejszą liczbę danych autor brał za okres tydzień. Można więc sobie wyobrazić, że miesięczna lub tygodniowa stopa zwrotu posiada trajektorię, która jest okresowa przez czas odpowiedni dla wybranego rynku, przebywając w pewnym "skorelowanym" obszarze. Po tym okresie destabilizuje się - przechodzi w całkowity chaos. Można byłoby powiedzieć, że początkowo raczej jest to trajektoria quasi-okresowa, bo wykryte cykle są cyklami przeciętnymi na przestrzeni lat i trudno mówić tu o pełnej periodyczności.

Jak powstają cykle i podcykle? Ułamkowość jest wszędzie. Część piąta

Dzisiejszy artykuł odwołuje się do wszystkich poprzednich części serii "Jak powstają cykle?" Poszukujemy uogólnionych czynników wpływających na ruchy cen akcji i wykorzystamy do tego wiedzę z poprzednich artykułów.

W pierwszej części artykułu "Jak powstają cykle?" pojawiał się często termin "preferencja" i "niepewność". Niepewność była wówczas rozumiana jako niezdecydowanie (a nie jako ryzyko). Należy zwrócić uwagę, iż pomimo związanego z tymi terminami subiektywizmu, ani "preferencja", ani "niepewność" nie niosą ze sobą zabarwienia emocjonalnego. Wprawdzie niezdecydowanie może wynikać ze sprzecznych emocji, ale równie dobrze z braku lub sprzeczności informacji (chyba że tymi informacjami są emocje).

Z drugiej strony od trzeciej części niniejszego cyklu przewija się wątek emocjonalny, gdzie chciwość i strach motywują do działania. Strachu nie należy mieszać z niepewnością. Strach jest lustrzanym odbiciem chciwości. Chciwość i strach są niemal tym samym. Anthony de Mello w książce "Przebudzenie" stwierdza, że pożądanie wynika w rzeczywistości ze strachu. Chciwość jest więc wtórna w stosunku do strachu. Jeśli czegoś (emocjonalnie) pragniemy, to prawdopodobnie dlatego, że się porównujemy z innymi. Jeśli czegoś nie posiadamy, co inni posiadają, a tego pragniemy, to czujemy się gorsi, co wywołuje lęk. A to jest źródłem chciwości. Ktoś powie: no jakże, przecież nauka ekonomii nie istniałaby, gdyby nikt nie chciał więcej niż ma. To prawda. Są wprowadzone do ekonomii pewne postulaty, na przykład, że im większy budżet, tym lepiej. Są też dobra nazywane dobrami pożądanymi - to te, które chcemy, czyli preferujemy. Jednak zwykłym ludziom trudno odróżnić tzw. preferencje od pożądania czegoś. Ekonomia mówiąc o preferencjach, stanowi jedynie o wyborze czegoś zamiast czegoś innego, szerzej - o wyborze ilości danego dobra względem ilości drugiego dobra. Celem jest maksymalizowanie użyteczności (i jednocześnie to jest definicja racjonalności). Nie mówi w ogóle o emocjach (a pożądanie to emocja). Dobro pożądane to tylko nazwa, nic więcej, wręcz myląca. Lepiej mówić o dobrach preferowanych i niepreferowanych. Ekonomia mówi o dążeniu jednostki do szczęścia, ale to szczęście może być opacznie rozumiane.

Świetne zrozumienie tej różnicy przychodzi po przeczytaniu "Przebudzenia". W jednym fragmencie de Mello odnosi się do czytelnika:

"Sądziłeś, ze szczęście to ekscytacja i dreszcze. Nieprawda, one tylko powodują depresję. Czy nikt ci o tym nie mówił? Jesteś podekscytowany, dobrze, ale właśnie torujesz sobie drogę do następnej depresji. Przy okazji w ten sposób pielęgnujesz kryjący się w tobie lęk."

Przychodzi tu niemal natychmiastowe skojarzenie z wahadłem, którego jeden silny ruch nieuchronnie prowadzi do ruchu w przeciwnym kierunku.

Gracze giełdowi, którzy szukają wrażeń, szybko wypadają z gry. W takim tonie wyraża się A. Elder (z zawodu psychiatra) w książce "Zawód-inwestor giełdowy". Podkreśla to również B. Graham w "Inteligentnym inwestorze". Często słyszy się też o maklerach, którzy dążą do szybkich pieniędzy i szybkiej kariery, lecz żyją w tak dużym napięciu, że po paru latach kompletnie wypalają się.

Paradoks polega na tym, że emocje mogą stać się również dobrem(!) Formalnie jednostka może wybierać tyle i tyle chciwości, tyle i tyle strachu. Brzmi to niedorzecznie, ale z ekonomicznego punktu widzenia nie ma przeszkód. Żywym przykładem mogą być aktorzy filmowi, którzy wywołują u siebie różnorakie stany emocjonalne. Wiedzą oni dobrze, że nie mogą to być zbyt słabe stany, żeby ich rola nie była zbyt "płaska", ale też nie mogą być skrajne, bo prowadzi to do przesady. To czy są to rzeczywiście jakieś emocje, czy tylko udawanie, pozostawiam na boku.

Problem polega na tym, że silne emocje prowadzą bardzo często do popełniania błędów przy różnych decyzjach. Wynika z tego, że jednostka dążąca do silnych emocji preferuje popełniać błędy. Oczywiście popełnianie błędów jest efektywne, gdy prowadzi do uczenia się czegoś. Ale w tym przypadku celem nie jest uczenie się, ale właśnie samo popełnianie błędów, co staje się coraz bardziej niedorzeczne. Co więcej, popełnianie błędów w niektórych sytuacjach musi prowadzić do nieracjonalności. Załóżmy, że człowiek jest pod wpływem silnej emocji i podejmuje jakąś decyzje, ale wiadomo jednocześnie, że gdyby tych emocji nie było, podjąłby inną decyzję. Emocje nie wpływają na obiektywną sytuację, w jakiej znajduje się ta osoba, a jednak zmienia ona preferencje tylko w zależności od tego, czy emocje nią rządzą czy nie. Oznacza to niespójność preferencji, wręcz nielogiczność - co jest właśnie błędem - a więc brak racjonalności.

Ale i z tej opresji można jakoś wyjść. Ten nieracjonalny człowiek powie po prostu, że on preferuje być nieracjonalnym... W sumie czemu nie, tylko pytanie, czy rzeczywiście nie staje się on wtedy racjonalny. Można więc zadać pytanie czy zachodzi następujące paradoksalne twierdzenie:
jeśli ktoś preferuje być nieracjonalny, to zawsze będzie racjonalny.

Gdyby to twierdzenie było prawdziwe, prowadziłoby do niezłego zamieszania. Jeśli ktoś chce być nieracjonalny, to posiada względem siebie pewną preferencje, zgodnie z którą dokonuje decyzji, a więc paradoksalnie staje się racjonalny. Jeśli jednak pragnie nieracjonalności, a staje się racjonalny, to nie spełnia swoich preferencji i staje się tym samym nieracjonalny. Ale jeśli staje się nieracjonalny, to paradoksalnie faktycznie "udaje" mu się spełnić preferencje w postaci bycia nieracjonalnym... itd.

Jak widać konieczne jest powołanie do życia człowieka ograniczenie racjonalnego. Taki człowiek jest ułamkowo racjonalny, ma jakieś preferencje, ale nie maksymalizuje do końca swojej użyteczności. Ciągle tkwi w niezdecydowanym stanie na granicy racjonalności i nieracjonalności. Ale nie jest to człowiek nieracjonalny.

Przejdźmy od jednostki do zbiorowości. W części drugiej niniejszego cyklu starałem się, wykazać, że jednostki są niejako zmuszane przez rynek do zachowania ograniczenie racjonalnego. Spróbuję to przedstawić jeszcze ściślej. Załóżmy, że każdy inwestor jest w pełni racjonalny i dyskontuje każdą ważną rynkową informację. Widzieliśmy, że prowadzi to do sytuacji, że rynek staje się zupełnie nieprzewidywalny, kolejne stopy zwrotu stają się nieskorelowane, losowe. I znów paradoks: gdyby rzeczywiście każdy inwestor reagował na każdą informację, to między innymi skrupulatnie dokonywałby operacji statystycznych. A więc testy statystyczne wykazywałyby, że nie da się przewidzieć przyszłości. Obserwując takie dane nie byłoby sensu grać na giełdzie, jeśli posiadamy awersję do ryzyka (co jest cechą w sumie rozsądną, inaczej mówilibyśmy o naiwności graczy, a to "pachnie" nieracjonalnością - taki gracz szybko wypadłby z gry, a przecież nie preferuje takiej sytuacji). No chyba, że ktoś byłby nieracjonalny, co przeczy początkowemu założeniu. A więc następuje zahamowanie handlu. A jednak handel nie ustaje. To więc już dowodzi, że inwestorzy nie są w pełni racjonalni (niezależnie od tego czy stopy faktycznie są losowe, czy nie). Są więc co najwyżej ograniczenie racjonalni.

Powyższe "co najwyżej" można usunąć. Gracze nigdy nie będą całkowicie nieracjonalni, właśnie z tego powodu, który został wyżej przytoczony - zawsze można jakoś tłumaczyć swoje zachowanie i we własnych oczach pozostawać w miarę racjonalnym.

Są książki, w których stawia się tezy, że zbiorowość uczestników rynku jest w ogóle nieracjonalna. Taką tezę spotkamy na przykład u Tony'ego Plummera w "Psychologii rynków finansowych". Plummer stwierdza, że człowiek ma dwoistą naturę. "Z jednej strony każdy ma skłonność do postępowania samodzielnego i indywidualnego, zwaną również tendencją asertywną, z drugiej zaś każdego cechuje również tendencja integracyjna, w wyniku której powstaje pragnienie przynależenia do zbiorowości. Jako członkowie zbiorowości ludzie zachowują się inaczej niż postępowaliby w pojedynkę." Przyczyna tego ma być głęboko ukryta w naturze; w przyrodzie wszystko ma być wzajemnie uwarunkowane. "Jak wykazał Erich Jantsch [The Self-Organising Universe, Pergamon, Oxford 1980], wychodząc od ustaleń fizyki kwantowej, cała przyroda składa się z wielopoziomowych struktur. Każdy poziom w tej hierarchii jest w stanie organizować niższe poziomy i wykorzystywać je dla swoich celów. W konsekwencji, każdy poziom posiada zdolność zachowywania własnej tożsamości, pomimo zmian swoich indywidualnych składników."
Ludzie więc tworzą zbiorowość, która stanowi nową jakość, nowy organizm, posiada własny "umysł", zdolność do samoorganizacji. "Istotną cechą każdego systemu posiadającego zdolność organizowania się - niezależnie od tego, czy będzie to zbiorowość, czy organizm żywy - jest fakt jego oscylowania w czasie przekazywania energii i informacji. Oscylacje te kształtują cykl życia zbiorowości: narodziny, dojrzałość i śmierć.

"Zbiorowość powstaje w wyniku pewnej zmiany wywołanej przez określoną informację oraz dzięki swej zdolności do zorganizowanej reakcji na tę zmianę." "Podczas fazy rozwoju zbiorowość wykazuje pełną zdolność do zachowania swojej integralności, nawet w obliczu nieprzyjaznego otoczenia."

"W okresie swej dojrzałości zbiorowość zaczyna jednak interesować się głównie własną egzystencją, przez co staje się mało elastyczna. Zdobywa poczucie pewności siebie, pławi się w blasku swych osiągnięć i dąży do kontrolowania twórczych poczynań swoich członków."

"W końcu okazuje się, że na skutek owej sztywności struktury zbiorowość nie jest już w stanie przystosowywać się do zmian otoczenia. Oczekiwania zbiorowości nie zmieniają się i w coraz większym stopniu okazują się rozbieżne z rzeczywistością. Wówczas zaczyna się rozpad, którego oznakami są wewnętrzne spory (...) W końcu przychodzi wstrząs, który doprowadza do całkowitego rozpadu zbiorowości. Jej cykl życiowy w ten sposób domyka się, a należące do niej jednostki mogą stać się członkami innych zbiorowości. A zatem mamy tu do czynienia z ciągłym procesem odradzania się, w którym po śmierci przychodzą narodziny." (Op. cit. T. Plummer, Psychologia rynków finansowych. U źródeł analizy technicznej, s. 10, 29-31.)

Pod względem nauki o kształtowaniu się zbiorowości i złożonych struktur, warto przeczytać tę książkę. Ale czy to rzeczywiście można przenieść na ruchy akcji? Przede wszystkim należy zauważyć, że zbiorowość jako pewna zorganizowana struktura tworzy się dlatego, że siła (użyteczność) zbiorowości jest wyższa niż siła (użyteczność) sumy jednostek ją tworzących. Pod tym względem rzeczywiście rynek zdobywa siłę, kształtuje się trend. To jest to, o czym pisałem w drugiej części cyklu, że inwestorzy niejako sami się racjonalizują. Aby utrzymać organizm przy życiu komórka musi współpracować z innymi komórkami.

Jednak istnieje tu maleńka różnica, która sporo zmienia. Ta komórka, która częściowo tworzy organizm komunikuje się z innymi komórkami i dokładnie "wie", co zrobią inne. Jednocześnie sama jest od nich zależna. W społeczeństwie też od siebie zależymy. Kiedy idę do sklepu, wiem mniej więcej co zastanę i łatwo mogę przewidzieć, jak zachowa się wobec mnie ekspedient. On też łatwo może przewidzieć, co zrobię, to znaczy, że coś kupię, podejdę do kasy i wypłacę pieniądze. Społeczeństwo tworzymy, aby zwiększyć globalną użyteczność, ale jest to możliwe tylko wtedy, gdy następuje pewna synchronizacja pomiędzy jednostkami. Synchronizacja wiąże się z możliwością przewidywania tego, co zrobi druga jednostka.

A jak to jest na rynku kapitałowym? To rzeczywistość, w której jeden chce przechytrzyć drugiego. Oczywiście istnieją małe społeczności, które faktycznie sobie próbują pomóc, dostarczając różnych informacji (przykładem są fora internetowe). Ale ze względu na elektroniczną więź, siła tych społeczności jest słaba i nie ma (raczej) wpływu na ceny aktywów. W przeciwieństwie do faktycznych zorganizowanych zbiorowości, zbiorowość rynkowa jest niepewna tego, co zrobią jej członkowie.

Plummer stwierdza na początku, że ludzie mają w sobie sprzeczne tendencje do zachowania indywidualizmu i konformizmu. Można się w pełni z tym zgodzić. Ale konformizm czy inaczej tendencje integracyjne nie mogą przyćmiewać - jeśli chodzi o graczy giełdowych - tendencji asertywnych. Należy więc raczej mówić o kombinacji obydwu czynników.

Dlaczego więc trend się ustala? Pomijając czynniki fundamentalne, ludzie zachowują się podobnie, stosują podobne heurystyki, przeżywają podobne emocje, ponieważ są podobnie skonstruowani. Niektórzy szybciej się dostosowują do sytuacji na rynku, inni wolniej. Kiedy zacznie się ruch w danym kierunku, to ci szybsi będą znowu spekulować kolejny wzrost, a wolniejsi znowu po nich. W ekonomii wymieniane są dwa rodzaje okoliczności, gdy popyt rośnie, gdy cena rośnie. W pierwszym przypadku mówi się o tzw. popycie niefunkcjonalnym, który wynika z oddziaływania tzw. efektów zewnętrznych na użyteczność. Oznacza to, że użyteczność danego dobra może się zmieniać w zależności od zachowania się innych konsumentów. Jednym z zachowań nabywców jest wtedy efekt owczego pędu, który oznacza, iż popyt na dane dobro wzrasta dlatego, że inni konsumują to dobro. W drugim przypadku mówi się o tzw. popycie spekulacyjnym, który wiąże się z oczekiwaniami co kształtowania się cen w przyszłości. [R. Milewski, Podstawy ekonomii, W-wa 2002, s. 99]. Często ludzie mylą efekt owczego pędu z popytem spekulacyjnym. Pomiędzy nimi jest jednak znacząca różnica: efekt owczego pędu jest zjawiskiem emocjonalnym, zachowaniem co najwyżej ograniczenie racjonalnym; popyt spekulacyjny jest zachowaniem wykalkulowanym i może być całkowicie racjonalny. Łatwo się domyślić, że nie jest możliwe odróżnić jeden typ od drugiego, nie tylko na giełdzie. Każdy nabywca może odpowiedzieć, że to kupno było wykalkulowane, oszukując nie tylko pytającego, lecz także samego siebie.

Teraz możemy połączyć, to o czym powiedzieliśmy. Mamy już racjonalny czynnik w postaci niepewności, ograniczenie racjonalny czynnik w postaci chciwości (strachu). Każdy z tych czynników odniesiemy do zbiorowości rynku.

Na początku naszą giełdową przestrzeń fazową będą tworzyć dwie zmienne: na osi poziomej chciwość (po stronie ujemnej - strach) oraz na osi pionowej niepewność. Dostaniemy ten sam obraz cyklu granicznego, który dotyczył wahadła.



Na rynku panują równoliczne grupy A (popyt), B (0) i C (podaż). Coś sprawia, że kurs idzie w górę. Jest to impuls dla grupy B, aby rozpocząć efekt owczego pędu bądź popyt spekulacyjny. Niech "chciwość" będzie utożsamiona z zachowaniem grupy B. Zatem z punktu, w którym oś chciwości jest równa zeru, a oś niepewności jest maksymalna, B przesuwa się w kierunku wzrostu chciwości, co powoduje spadek niepewności. Gracze stopniowo zmieniają swoje preferencje, dostosowując je do sytuacji na rynku. Zauważmy, że zmieniają je pod wpływem emocji. W końcu chciwość jest tak wielka (stopa zwrotu też), że przyćmiewa całkowicie niepewność, która równa się 0. Ale zaraz potem niepewność znowu wzrasta, lecz w kierunku przeciwnym, co powoduje, że chciwość maleje. Stopa zwrotu ciągle jest dodatnia, ale spada. W końcu niepewność znowu osiąga max, a chciwość spada do zera. Jest to moment, gdy chciwość = strach, a stopa zwrotu jest zerowa. Od tej chwili następują spadki na giełdzie, a niepewność maleje. W końcu strach jest maksymalny i niepewność zerowa. Następnie ujemna stopa zwrotu maleje, a niepewność wzrasta. W końcu strach znów zrównuje się z chciwością, a stopa zwrotu powraca do zera. Cykl zaczyna się od początku.

Jeśli ten cykl graniczny umieścimy w wymiarze czasowym, to powstanie spirala w trzech wymiarach. Z punktu widzenia jednej ze zmiennych, na przykład chciwości, dostaniemy szereg czasowy, którego wykres jest po prostu sinusoidą:



Uważny czytelnik zauważył, że zrównaliśmy poziom chciwości ze stopą zwrotu. Inaczej mówiąc poziom chciwości utożsamiamy z wielkością zmiany kapitału na rynku. Dlaczego? Ponieważ poziom chciwości jest proporcjonalny do oczekiwanej stopy zwrotu przez uśrednionego gracza. Im większą oczekuje stopę zwrotu, tym (chętniej) więcej włoży kapitału w inwestycję.

Chciwość możemy również potraktować nie jako stopę zwrotu, ale jako warunkową oczekiwaną stopę zwrotu (warunkową wartość oczekiwaną stopy zwrotu). Wtedy model staje się uogólnieniem modelu rynku efektywnego - dla rynku efektywnego chciwość = strach = 0 (brak emocji, pełna racjonalność). Jedynie panuje maksymalna niepewność, a więc warunkowa oczekiwana stopa zwrotu = 0.

Gdyby rzeczywiście tak przyjąć, to taki model byłby wystarczający. Jednak chcemy stworzyć model z rzeczywistymi zmianami, a nie tylko oczekiwanymi. Jeśli jednostki są ułamkowo racjonalne, to z pewnością nie będą się zachowywać jak nieracjonalna zbiorowość w sensie Plummera. Będą starać się wykorzystywać każdą możliwość, by zarobić, ale jednocześnie będą pod wpływem zachowań innych graczy. Gdyby byli taką Plummerowską zbiorowością, szybko zdyskontowaliby wiedzę o "narodzinach", "dojrzałości" i "śmierci" zbiorowości. Coś takiego jest iluzją. Jeśli już mówić o istnieniu pewnej zorganizowanej struktury, to nie w sferze realnej, lecz abstrakcyjnej (istnieje niewidzialna nić połączeń pomiędzy jednostkami oparta na emocjach i heurystykach). Umożliwi to model chaotyczny. Założymy, że ruch cen akcji odbywa się w czasie ciągłym. Wtedy musimy uwzględnić trzecią zmienną w przestrzeni fazowej, aby możliwe było wywołanie chaosu.

Niech trzecią zmienną stanowi czynnik fundamentalny. Wcześniej utożsamialiśmy ten czynnik z grupą D. W zależności od wielkości grupy D, wywoływała ona większy lub mniejszy impuls, który znowu stawał się efektem motyla dla grupy B. Czynnik fundamentalny możemy, podobnie jak to uczyniliśmy z "chciwością", określić jako zmianę wartości zmiany kapitału, czyli zmianę stopy zwrotu (dynamika kapitału zależy od ogólnej koniunktury gospodarczej). Analogią jest tu prędkość i przyspieszenie. Prędkość to zmiana drogi w czasie, przyspieszenie to zmiana prędkości w czasie, czyli zmiana tej zmiany drogi w czasie.

Jeśli więc trzy podukłady - zmiana wartości kapitału, zmiana wartości tej zmiany oraz niepewność nie będą ze sobą synchronizować, pojawi się ruch chaotyczny.

Nie wiadomo jednak, jak taki atraktor chaotyczny wygląda. Może przypomina dziwny atraktor wirnika? Poniżej przedstawiono dwa przykłady chaotycznych portretów fazowych (projekcji atraktora na wybrane osie współrzędnych) dla drgań wirnika z dwóch różnych perspektyw i odpowiadający przebieg czasowy jednej ze zmiennych.





[Rysunki wzięte z U. Ferdek, Wpływ zderzeń na drgania poprzeczne i skrętne wirników, Czasopismo techniczne, 1-M/2008, s. 93].

W następnym, czyli ostatnim odcinku z serii "Jak powstają cykle?" poruszymy meritum sprawy, tj. istnienie cykliczności i podcykliczności trajektorii w układach chaotycznych.