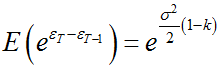Smarujący estymator

Poprzednio pokazałem, że gdy przyjmiemy model geometrycznego procesu ruchu Browna (model ceny aktywa):

(1)

oraz wiedząc, że parametr b jest nieznany, tak że możemy jedynie oszacować jego wartość na podstawie próby losowej, to wartość oczekiwana stopy zwrotu (R) może być oszacowana za pomocą modelu:

(2)

gdzie b z falką to estymator MNK z modelu ln(P) = b*T + składnik losowy.

Wyraz k wyraża błąd retransformacji z postaci liniowej do nieliniowej (pierwotna jest postać nieliniowa, która jest transformowana do liniowej przez logarytmowanie, aby zastosować MNK; następnie powracamy do postaci nieliniowej, czyli dokonujemy retransformacji). Jak widać przy nieco większym T, wyraz k ma bardzo mały wpływ.

Geometryczny ruch Browna zakłada jednak rozkład log-normalny. Z tym rozkładem jest ten problem, że jego lewy ogon bardzo szybko zbiega do zera:

W rzeczywistości dobrze wiemy, że na giełdach zdarzają się rzadkie, ale bardzo silne odchylenia, a także asymetria. Kwartalny sWIG80 od 01.1994 do 03.2016 (87 obserwacji) miał minimum na poziomie -40%, a maksimum prawie +54%. Poniżej jest wykres oszacowanego rozkładu sWIG80 (zrobiony w Gretlu za pomocą jądra Gaussa - metoda ta daje zniekształcony obraz, bo sugeruje, że wystąpiły wartości poniżej -40%, co jest nieprawdą):

W tym wypadku lepszy okazuje się rozkład normalny, choć występuje tu pewna prawostronna skośność.

Duan [1] przedstawił metodę retransformacji, która nie zakłada z góry żadnego rozkładu. Duan nazwał swój estymator "smarującym estymatorem" (smearing estimate). Pokazał, że jego estymator daje lepsze rezultaty, tzn. jest bardziej efektywny, gdy rozkład stopy zwrotu nie jest log-normalny, a więc gdy logarytmiczna stopa zwrotu nie posiada rozkładu Gaussa. 

Smarujący estymator (SE) dla oczekiwanej stopy zwrotu można zapisać następująco:

(3)

Wariancja składnika losowego jest tym razem stała w czasie, czyli występuje jednocześnie  homoskedastyczność i stacjonarność składnika losowego. Składnik losowy jest tutaj różnicą pomiędzy sąsiadującymi składnikami losowymi modelu logarytmicznej ceny, dlatego że pierwotny składnik losowy w modelu (1) jest niestacjonarny (porównaj zapis wariancji w obu przypadkach). Oczekiwana stopa zwrotu powstała po prostu przez zapis:

Nic więc dziwnego, że aproksymacją będzie:

(4)

Korekta Duana to zwykła średnia arytmetyczna kolejnych stosunków reszt z regresji liniowej. 

Gdy rozkład log-stopy jest normalny i znamy pełną populację to (4) sprowadza się do:

oraz gdy jest normalny i nie znamy pełnej populacji, to z modelu (2) wynika, że:

Model (3) można więc traktować jako uogólnienie (2). Trzeba jednak zaznaczyć, że oryginalny wzór Duana jest nieco bardziej ogólny niż ten, który podałem w (3): w naszym przypadku rolę zmiennej objaśniającej pełni zmienna czasowa, która się redukuje, natomiast w oryginale jest zastąpiona zmienną x, która może być dowolna (wtedy też w modelu (3) ocena parametru b z falką będzie przemnożona dodatkowo przez x).

Model (3) pozwala też zrozumieć zależności pomiędzy średnią warunkową a niewarunkową. Jeżeli nie istnieje liniowa korelacja między okresem T a logarytmiczną ceną ln(P), czyli gdy ocena b = 0 w modelu (1), to oczekiwana stopa zwrotu w (3) sprowadza się do zwykłej średniej arytmetycznej:

Przykład.

Aby porównać model (2) z (3), użyję tych samych danych co poprzednim razem, tj. dla mbanku - rocznie 1994-2015 (22 obserwacje). Nie będę się wgłębiał w to czy stopy mbanku są normalne, lognormalne czy jeszcze inne. Zaczynamy od zlogarytmowanego modelu (1):

Parametr b wyniósł 11,18%. Korzystając z Gretla uzyskałem reszty powyższej regresji liniowej, które podstawiłem do wzoru (4), czyli korekty SE. Korekta ta wyniosła 1,0699. Podstawmy to do (3):

Dla porównania stosując model (2) uzyskałem wielkość 18.69%, natomiast dla standardowego wzoru na wartość oczekiwaną w rozkładzie lognormalnym (czyli dla k = 0) 18.73%. Dodatkowo przypomnę, że średnia arytmetyczna wyniosła 20,08%, a geometryczna 11,71%. Pamiętać trzeba, że geometryczna średnia dotyczy tylko inwestycji długoterminowej, dlatego SE staje się konkurencyjny głównie w stosunku do średniej arytmetycznej (która będzie poprawna w sytuacji, gdy logarytmiczna cena nie jest liniowo skorelowana z okresem czasu) oraz do estymatora z (2) (który jest poprawny dla próby w rozkładzie log-normalnym).

Literatura:

[1] N. Duan, Smearing Estimate: A Nonparametric Retransformation Method, Sep. 1983

Transformacja lognormalnego modelu z nieznanym parametrem

Problem estymacji parametrów nieliniowych funkcji losowych poprzez przekształcenia liniowe jest znany w statystyce od dawna i ma bogatą historię. Zajmowali się nią Barlett [1], Quenouille [2], Neyman i Scott [3], Box i Cox [4], Hoyle [5], Granger i Newbold [6], Duan et al. [7], Taylor [8] i wielu innych. W szczególności transformacjami rozkładów lognormalnych zajmowali się Finney [9],  Mostafa i Mahmoud [10], Meulenberg [11], Goldberger [12], Bradu i Mundlak [13] , Heien [14], Teekens oraz Koerts [15], Evans i Shaban [16], Duan [17].

Zacznijmy ponownie  od modelu, który opisałem w Czy mediana jest lepsza od średniej?, tj. proces geometrycznego ruchu Browna, jednak dla uproszczenia pomińmy stałą, która nie ma tutaj wpływu na analizę:

(1)

Logarytmując model (1) uzyskujemy funkcję liniową, co pozwala nam na użycie MNK:

Wiemy już, że prosta delogarytmizacja ostatniego równania nie prowadzi do otrzymania wartości oczekiwanej P(t). Aby ją uzyskać, musimy wykorzystać własności rozkładu lognormalnego. Składnik losowy z początkowego założenia ma rozkład normalny, wobec czego exp(składnik losowy) ma rozkład lognormalny. Ale co z parametrem b? Dotychczas dla uproszczenia zakładaliśmy, że b jest znane. W rzeczywistości nie znamy parametru b. Jeżeli nawet b jest nieznane, to ciągle pozostaje stałą, wobec czego wartość oczekiwana zmiennej lognormalnej pozostaje jak w poprzednich rozważaniach:

(2)

W rzeczywistości b jest nieznane, bo operujemy zawsze na pewnej próbie losowej, a więc szacowany parametr będzie się zachowywał jak zmienna losowa (dla danego okresu) o pewnej wartości oczekiwanej i wariancji. Trzeba zauważyć, że w ekonometrii mamy 2 rodzaje wartości oczekiwanych: dla stałej wartości (w populacji) oraz dla zmiennej losowej (w populacji i w próbie). W pierwszym przypadku mamy do czynienia po prostu z prawdziwym parametrem istniejącym de facto dla pełnej populacji. Jednak próbki z tej populacji będą losowe i będą kreować statystyki, jak średnia i wariancja. Dopiero przy bardzo dużej liczebności próbki, wariancja będzie spadać do zera, tak że pozostanie tylko średnia, która zbliży się do prawdziwego parametru i w ten sposób wartość oczekiwana zmiennego parametru z próby będzie się równać prawdziwemu (stałemu) parametrowi. W drugim przypadku wartość oczekiwana dotyczy zmiennej losowej niezależnie czy myślimy o próbie czy populacji. Wtedy próbki losowe będą kreować własne rozkłady, ale wraz z wielkością próby będą zbliżać się do rozkładu z populacji, podobnie jak w pierwszym przypadku. Jednakże  tym razem wariancja nie będzie już spadać do zera wraz z liczebnością próby.

Niezależnie od tego czy mówimy o pierwszym czy o drugim przypadku, zawsze określenie "wartość oczekiwana" będzie się odnosić do średniej z populacji. Wartość oczekiwana parametru b będzie więc równać się prawdziwemu parametrowi.

Przyjmiemy pierwszy przypadek. Chociaż moglibyśmy przyjąć drugą możliwość - z parametrem jako zmienną losową - to czyniłoby to analizę znacznie bardziej skomplikowaną. Dlatego przyjmiemy standardowy punkt widzenia - czyli że istnieje tylko jeden prawdziwy parametr, ale dążymy do jego uzyskania na podstawie prób losowych. Oznacza to, że parametr b jest stały, więc model (2) jest nadal poprawny.

Formalnie rzecz biorąc model (1) stanowi model dla całej populacji. Stąd również model (2) dotyczy całej populacji. Jeżeli więc tworzymy model w oparciu o próbę losową, to nasze parametry zaczynają już się wahać, stają się zmiennymi losowymi, a przez to, aby zachować formalność, musimy te zmienne jakoś inaczej oznaczyć, aby odróżnić je od prawdziwych (stałych) parametrów. Oznaczymy je daszkiem. Uzyskamy więc na podstawie próby losowej cenę z daszkiem, parametr b z daszkiem, a nawet składnik losowy z daszkiem, bo ogólnie rzecz biorąc może on się inaczej zachowywać niż prawdziwy składnik losowy z populacji. Mówiąc krótko, estymujemy model (1) za pomocą:

(3)

Ponieważ składnik losowy ma rozkład normalny, to zmienna b także. Naszym zadaniem jest teraz znaleźć wartość oczekiwaną ceny z daszkiem. Pamiętajmy jednak czym jest cena z daszkiem - to losowa prognoza ceny. Zatem szukamy oczekiwanej prognozy ceny. Zmienna b z daszkiem jest ciągle zmienną losową o rozkładzie normalnym, zatem exp(bt) ma rozkład log-normalny, czyli cena z daszkiem ma rozkład log-normalny. A więc szukamy wartości oczekiwanej zmiennej o takim rozkładzie. Wzór na nią jest znany. Wzór ten zawiera w sobie wartość oczekiwaną b z daszkiem oraz wariancję b z daszkiem. W naszym wypadku zakładamy, że wariancja współczynnika b jest znana, tzn. jest równa wariancji współczynnika b z daszkiem. Z własności wartości oczekiwanej i wariancji wiemy, że

, ponieważ czas t jest oczywiście stałą.
Całkowity model z wartością oczekiwaną to przekształcenie z (3)

(4)

Zwróćmy uwagę, że wariancja składnika losowego jest funkcją czasu, a nie stałą - w każdym kolejnym okresie się zwiększa.

Aby nie mylić jednostek czasowych ze zmienną, t zastąpimy ostatnim okresem T. Ponieważ wariancja składnika losowego sumuje się w czasie, zapiszemy ją jako średnią wariancję przemnożoną przez T:

(5)

Aby uprościć model (5), wykorzystamy dwa znane wzory: na ocenę parametru b z daszkiem oraz wariancję parametru b z daszkiem. (Oba można znaleźć np. w Uriel [18], wzory 2-37 + 2-64). Pierwszy to estymator MNK dla b, który oznaczymy jako b z falką, w sytuacji gdy stała w modelu liniowym jest równa 0:

(6)

Jednak sumę kwadratów liczb naturalnych można wyrazić za pomocą (zob. np. http://www.trans4mind.com/personal_development/mathematics/series/sumNaturalSquares.htm):

(7)

Stąd:

(8)

Drugi wzór - na wariancję współczynnika b pokażemy od razu wykorzystując wzór (7):

(9)

Wariancja ta nie zawiera już falki, bo z początkowego założenia była znana. Ponieważ wariancja składnika losowego jest znana, to podstawiamy (9) do (5):

(10)

Uzyskaliśmy ocenę wartości oczekiwanej ceny. W końcu przypomnijmy, że (2) można zapisać:

(11)

 Co oznacza, że nasz model (10) będzie go przypominał wraz ze wzrostem liczebności próby T:

 Inaczej mówiąc:

Ale tak będzie tylko w przypadku, gdy T jest duże. Trzeba w tym miejscu mocno uświadomić sobie co to oznacza. Model (10) jest wartością oczekiwaną prognozy ceny (prognoza ceny jest zmienną losową). Oczekiwana prognoza ceny jest pewną średnią opartą na obserwacjach historycznych. Tymczasem model (11) jest wartością oczekiwaną samej ceny. Dopiero w długim okresie model (10) zrówna się z modelem (11). Tak nakreślona sytuacja pozwala nam określić kryterium, za pomocą którego wybierzemy jedną z tych dwóch wartości oczekiwanych. Czy chcemy odnaleźć wartość oczekiwaną z próby losowej czy wartość oczekiwaną z populacji. Wcześniej jednak stwierdziłem, że mówiąc o wartości oczekiwanej mam na myśli zawsze średnią w populacji, jeśli więc dotyczy próby, to nie jest to wartość oczekiwana. Wynika z tego, że model (10) jest estymatorem obciążonym wartości oczekiwanej ceny. Nie jest wcale oczywiste, że obciążony estymator należy odrzucić. Ważniejsza jest efektywność estymatora. W tym przypadku mniejszą wariancję posiada jednak estymator nieobciążony wartości oczekiwanej ceny - model (11), który nas interesuje (widać, że w modelu (10) współczynnik f jest dodatni, więc powiększa wariancję, więc jest gorszy). Problem leży w wyłuskaniu jego empirycznej postaci.

Problem ten rozwiązuje Meulenberg [11]. Zauważa on, że model (10) jest modelem empirycznym, a więc to on będzie punktem zaczepienia. Pomiędzy modelem (10) a (11) istnieje pewna relacja. Na początku przecież stwierdziłem, że wartość oczekiwana zmiennej b z daszkiem będzie równa b, czyli:

(12)

Ale wtedy dla dowolnego T można będzie (10) zapisać:

(13)

 A wtedy (13) można przekształcić:

 I w ten sposób dostajemy równanie na poszukiwaną E(P):

(14)

Co wstawić za E(P z daszkiem)? Meulenberg stwierdził, że (10), a więc także (13) jest modelem empirycznym, a więc już zawierającym parametry obliczone MNK. Zauważmy jednak do czego to prowadzi. Jest to najtrudniejszy moment w teorii, więc powtórzmy. Zaczynamy od modelu (3), logarytmujemy i z liniowego modelu wyznaczamy poprzez MNK empiryczne b, które oznaczamy jako b z falką. Ale b z falką jest stałą (w przeciwieństwie do b z daszkiem), a nie zmienną losową. Jeżeli więc teraz podstawimy tę stałą do modelu liniowego, to retransformacja do modelu wykładniczego (3) i wyznaczenie wartości oczekiwanej wykładniczego modelu (3) nie będzie zawierać składnika f, związanego z wahaniami estymacji. Zatem wartość oczekiwana z (3) stanie się prostym modelem:

 (15)

Pomysł Meulenberga polega na zrównaniu modelu (13) z modelem (15). Później przeanalizujemy czy jest on trafny.

(16)

Przekształcając:

Co daje:

(17)

Stąd:

(18)

Czyli:

(19)

Lub w nieco prostszym ujęciu:

(20)

Model (20) jest tym, czego szukaliśmy: zawiera wszystkie składniki gotowe do użycia w regresji liniowej MNK. Pozostaje jeszcze kwestia wariancji. Do jej estymacji może służyć zwykła wariancja logarytmicznej stopy zwrotu, ale formalnie należy użyć tzw. błędu standardowego reszt, będącego pierwiastkiem wariancji składnika resztowego (formalność wynika z ciągłości użytej funkcji).

Podobnie jak to wcześniej analizowaliśmy, gdy T rośnie, błędy związane z przekształceniem funkcji liniowej w wykładniczą tracą coraz bardziej na znaczeniu, tak że w dużej próbie b z falką stanie się bliskie prawdziwemu parametrowi b (a więc k spada do zera).

Teraz przeanalizujemy trochę dokładniej sposób Meulenberga, ponieważ wcale nie jest jasne utożsamienie (13) z (15). Wróćmy jeszcze raz do tej równowagi w (16) i przekształćmy inaczej:

(21)

W końcu, biorąc pod uwagę zapis (20) trzeba zauważyć, że (21) można zapisać:

(22)

Zwróćmy uwagę na (22): odejmuje się tu pewną zawyżoną część wariancji, aby zrównać ocenę parametru z prawdziwym parametrem b.

Warto jeszcze raz odróżnić ocenę wartości oczekiwanej od tej wartości:

Zazwyczaj mniej lub bardziej świadomie popełnia się ten błąd, że prawdziwy parametr b jest równy ocenie tego parametru, czyli b z falką. Formalnie rzecz biorąc nie można więc podstawić b z falką ani do modelu (2) ani (10). Podstawienie b z falką do (16) wynika wyłącznie ze stwierdzenia, że b z falką już zawiera w sobie zawyżoną kapitalizację wskazując tym samym na jej pochodzenie od zmiennej losowej. Prosto mówiąc: wiem, że (13) jest zawyżone oraz wiem, że (15) jest zawyżone, ale też wiem, że obydwa pochodzą od tego samego modelu (3) - wobec tego zakładam, że mogę je ze sobą zrównać. Oto wyjaśnienie zapisu (16), który wydaje się teraz sensowny.

Ostatecznie widać jaki błąd wywołuje retransformacja z modelu liniowego do nieliniowego:
błąd ten bierze się stąd, że ocena parametru b ulega procentowym zmianom w czasie, jest zmienną losową, natomiast prawdziwy parametr jest stały w czasie. Gdyby ocena była stałą liczbą, błąd ten nie wystąpiłby.

Faktycznie, nie jest to prosty temat. Przyda się przykład.



Przykład.
Na podstawie wzoru (20) nie trudno zauważyć, że duża liczebność obserwacji sprawia, że błędy retransformacji nie mają praktycznie żadnego znaczenia. Dlatego najlepszym sprawdzianem będzie niewielka próbka. Weźmy roczne dane mbanku od końca 1994 do końca 2015 r. i są to 22 obserwacje.

Statystyki stopy zwrotu:
średnia = 20,08%
mediana = 12%
średnia geometryczna = 11,71%
odch. standardowe = 45,5%

Tworzymy model (1):

Logarytmujemy:

Uzyskujemy:

Obliczamy parametr regresji b w KMNK. Uzyskałem 11,18%. Błąd standardowy reszt (tj. odchylenie standardowe składnika losowego) wyniósł 34,6%. Następnie stosujemy (20) dla oczekiwanej stopy zwrotu:

gdzie R to stopa zwrotu jako zmienna losowa.
Podstawiamy:

Porównajmy wynik ze standardowym wzorem dla k = 0:

Błąd retransformacji wynosi 0.04%.

Dwie uwagi. Po pierwsze warto zauważyć jak należy używać wariancji. Wariancja składnika losowego liczona jest jako suma kwadratów składnika losowego podzielona przez liczbę obserwacji (22) pomniejszoną o liczbę stopni swobody (2). Nie jest to więc zwykła wariancja, gdyż dotyczy modelu liniowego. Nie jest to też zwykła wariancja logarytmicznych stóp zwrotu.

Po drugie zwróćmy uwagę, że użyłem modelu ze stałą. Model empiryczny tego wymaga, gdyż bez stałej zakładamy, że jest ona równa zero, czyli, że P(0) = 1. To spowodowałoby błędne nachylenie linii regresji. Trzeba jednak pamiętać, że wzór (7) zakładał właśnie brak stałej.  Dlaczego więc można stosować ciągle wzór (20)? Oczywiście dlatego, że interesuje nas stopa zwrotu brutto M, czyli stopa netto R. A ta rzecz jasna nie może zależeć od poziomu stałej.


Literatura:
[1] M. S. Bartlett, The Use of Transformations, Mar 1947
[2] M. H. Quenouille, Notes on Bias in Estimation, Dec 1956
[3] J. Neyman, E. L. Scott, Correction for Bias Introduced by a Transformation of Variables, Sep 1960
[4] G. E. P. Box, D. R. Cox, An Analysis of Transformations, 1964
[5] M. H. Hoyle, Estimating Generating Functions, Nov 1975
[6] C. W. J. Granger, P. Newbold, Forecasting Transformed Series, 1976
[7] N. Duan, W. G. Manning, Jr., C. N. Morris, J. P. Newhouse, A Comparison of Alternative Models for the Demand for Medical Care, Apr 1983
[8] J. M. G. Taylor, The Retransformed Mean After a Fitted Power Transformation, Mar 1986
[9] D. J. Finney, On the Distribution of a Variate Whose Logarithm is Normally Distributed, 1941
[10] M. D. Mostafa, M. W. Mahmoud, On the Problem of Estimation for the Bivariate Lognormal Distribution, Dec 1964
[11] M. T. G. Meulenberg, On the Estimation of an Exponential Function, Oct 1965
[12] A. S. Goldberger, The Interpretation and Estimation of Cobb-Douglas Functions, 1968
[13] D. Bradu and Y. Mundlak, Estimation in Lognormal Linear Models, Mar 1970
[14] D. M. Heien, A Note on Log-Linear Regression, 1968
[15] R. Teekens, J. Koerts, Some Statistical Implications of the Log Transformation of Multiplicative Models, Sep 1972
[16] I. G. Evans, S. A. Shaban, A Note on Estimation in Lognormal Models, Sep 1974
[17] N. Duan, Smearing Estimate: A Nonparametric Retransformation Method, Sep. 1983
[18] E. Uriel, The simple regression model: estimation and properties, 09-2013
 
http://www.trans4mind.com/personal_development/mathematics/series/sumNaturalSquares.htm

Szybkie porównywanie statystyk w Wolphram Alpha

Jeśli nie mamy za bardzo czasu na głębsze analizy makroekonomiczne, ale chcielibyśmy uzyskać szybko wskaźniki porównawcze, możemy posłużyć się narzędziem Wolphram Alpha (WA). WA służy głównie do rozwiązywania różnych, często skomplikowanych problemów matematycznych, ale jego użyteczność na tym się nie kończy. Powiedzmy, że najpierw chcę sprawdzić jak się zachowuje wzrost PKB w Polsce. Wpisuję np. "gdp growth poland" i wciskam Enter:

Dalej, np. chcę porównać wzrost PKB w Polsce ze wzrostem PKB w USA. Wpisuję w wyszukiwarce WA np. "poland gdp growth vs usa gdp growth":

Wpiszmy "Poland unempoyment rate vs GDP growth rate":

Jeśli chodzi o dane ekonomiczne, WA nie jest jakimś wybitnym narzędziem, bo wielu bardziej szczegółowych rzeczy nie znajdziemy (np. gdy chciałem znaleźć porównanie danych kwartalnych, to nie dostałem tego co chciałem). Najlepsze statystyki dostaniemy, gdy porównamy pewne ogólne cechy, np. wpiszemy "Poland vs Germany":

Niektóre statystyki pominąłem.
Nawiasem mówiąc, biorąc pod uwagę tzw. Kryzys Migracyjny , tj. ciągły napływ uchodźców np. do Niemiec, dość interesujące, że w Niemczech aż 91% populacji to ciągle Niemcy, a więc niewiele mniej niż Polaków w Polsce (96%) - dane są z 2014 r. Dalej, patrząc na religię, o ile Polska to niemal w 100% kraj katolicki, o tyle Niemcy są w dużej mierze ateistami, stąd tylko 76% uważa się za chrześcijan, natomiast islam stanowi tylko 4,5%. Język natomiast już w ogóle tak jak w Polsce jest niemal w 100% "rdzenny".

WA można także wykorzystać do wielu analiz statystycznych. Np. wpisanie "z-test for population mean", dostarczy szczegółowej analizy statystyki z. Wybieramy dane do testu, np.

I otrzymujemy takie informacje:

co oznacza, że (zakładając rozkład normalny) jeśli liczba obserwacji = 100, a średnia z próbki wynosi 0,2 i odchylenie standardowe = 1, to hipoteza sprawdzająca czy średnia z populacji wynosi 0, zostanie odrzucona na poziomie istotności 5%, ponieważ p-value = 4,55% < 5%.

Następnie, łatwo sprawdzić regresję liniową, którą można prosto ułożyć stosując np zapis: linear fit {34, 20},{40, 23},{48, 22},{52, 29},{57, 27.5}, {62, 31}

WA podaje wiele innych przykładów funkcji statystycznych (np. przedział ufności dla średniej i odchylenia standardowego) i ekonometrycznych (np. "exponential fit" czy "log fit").

Na koniec, jako ciekawostkę, dodam, że jest też możliwość użycia CAPM: