Bessa w USA nie udzieli się Polsce???

Post ten ten jest odpowiedzią na artykuł Czy bessa w USA udzieli się Polsce?, który pojawił się 10.02 na całkiem niezłym, choć trochę zbyt amatorskim blogu. Z owego artykułu dowiadujemy się, że:

• Nadejście bessy w USA nigdy nie spowodowało nadejścia bessy w Polsce. Co więcej czasem to właśnie Polska pierwsza zaczynała spadać, a dopiero później dołączały Stany. 
• Bessy w Polsce zawsze pojawiały się w towarzystwie słabych danych makro z kraju.

 A później czytamy:

Na pytanie o zawalenie się naszej giełdy mamy jasna odpowiedź nieco wyżej mówiącą że: Jeszcze nigdy bessa w USA nie wywołała bessy w Polsce. Ta odpowiedź sugeruje, że nie musimy martwić się, o "przeciągającą się" hossę w USA jeśli inwestujemy w Polsce.

 Dzięki uzyskanej wiedzy w artykule Czy trój-betowy CAPM wyjaśnia stopy zwrotu? wiemy już, że istnieje teoretyczny związek pomiędzy dochodami z pracy a oczekiwaną stopą zwrotu z akcji na rynku kapitałowym. Wiemy także, że istnieje empiryczna zależność pomiędzy stopami zwrotu a dochodami z pracy. Należy tu dokładnie zrozumieć, że mówimy o dochodach z pracy,a zatem nie wliczamy żadnych dochodów z inwestycji kapitałowej. Oznacza to, że dochody z pracy nie mogą być utożsamiane z PKB. PKB uwzględnia wszelkie dochody. Od PKB trzeba by odjąć wszystkie dochody pochodzące spoza pracy: dywidendy (jeśli nie są rekompensatą za wynagrodzenie) oraz wszystkie zyski kapitałowe.

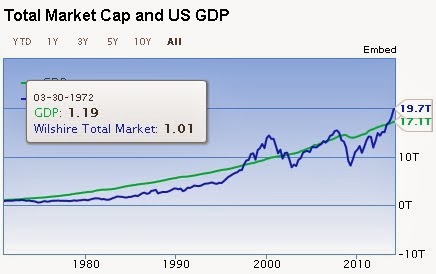
Dla uproszczenia obliczeń, przyjmę jednak, że dochody z pracy jest to PKB. Ale musimy pamiętać, że nie jest to dobre przybliżenie, jeśli S&P500 stanowi dużą część PKB USA. A jaki jest obecnie stosunek SP500 do GDP? Na stronie http://www.gurufocus.com/stock-market-valuations.php
mamy odpowiedź. Najpierw spójrzmy na następujący wykres:

Teraz zobaczmy to samo, ale w stosunku procentowym obydwu indeksów:

SP500 obecnie przewyższa GDP o 15%. Tak więc S&P 500 ogólnie stanowi dużą część GDP, dlatego też korelacja pomiędzy nimi jest sama z siebie tautologiczna. Ma to też pewien związek ze strategią polegającą na kupowaniu akcji gdy ten stosunek jest mniejszy od 1 i sprzedawaniu gdy jest powyżej 1. Jeśli bowiem dziś akcje stanowią ponad 100% GDP, to znaczy, że GDP rośnie ogólnie wolniej niż SP500, co sprawia, że można uznać rynek za zbyt szybko rosnący, czyli jakby przewartościowany. Odwrotnie, jeśli SP500 do GDP < 1, to GDP rośnie ogólnie szybciej od SP500, co sprawia, że można uznać rynek za zbyt wolno rosnący, czyli jakby niedowartościowany. Tym samym otrzymujemy pewne wskazówki na rosnące niebezpieczeństwo inwestowania w akcje w USA.

Pytanie jednak jak się ma giełda USA do Polski? Możemy z dużą dozą pewności stwierdzić, że dane makro z Polski będą mieć wpływ na WIG. Ale czy amerykańskie PKB wpływa na WIG?

Pobrałem kwartalne PKB ze strony http://www.bea.gov/ aby obliczyć kwartalne stopy zmian PKB kw/kw (niezaanualizowane). Ze stooq.pl pobrałem dane S&P500 oraz WIG i policzyłem kwartalne stopy zwrotu kw/kw. Interesowały mnie lata od początku 2001 do ostatnich danych, czyli września 2013. Było to tylko 51 danych, ale wnioski można już wyciągać. Przy tak małej liczbie obserwacji poziom istotności 0,1 wystarczy.

To może po kolei. Korelacja Pearsona pomiędzy PKB USA i S&P 500 wyniosła 0,39, oczywiście istotna stat.  Jednakże z punktu widzenia regresji liniowej, zależność istnieje, p < 0,01, ale R^2 = 15%, R^2 adj. = 13,4%.

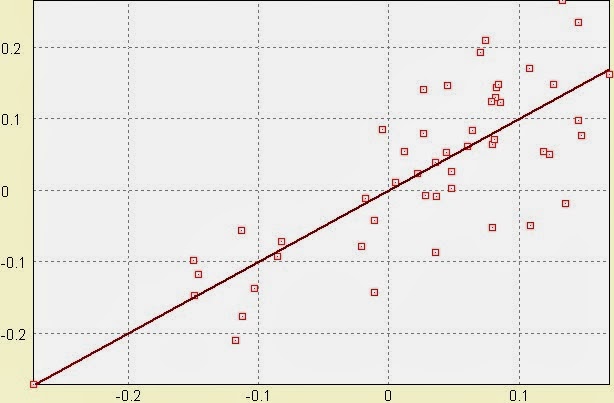
Jednak nas bardziej interesuje kwartalna zmiana WIG w relacji do kwartalnej zmiany PKB USA. Okazuje się, że korelacja Pearsona wynosi aż 0,44. W regresji liniowej również p < 0,01, R^2 jest wyższy niż dla SP500 i wynosi 19,55%, a R^2 adj.= 18%. Niski R^2 jest spowodowany dużym rozrzutem obserwacji wokół wartości oczekiwanej:

Ten empiryczny model ma następującą postać:

Oczekiwana stopa WIG(t) = -0.04 + 7.02*Stopa_zmian_PKB_USA(t)

Oczekiwaną i faktyczną stopę zwrotu z WIG możemy także porównać w perspektywie czasowej:

Nie ma żadnych wątpliwości, że PKB amerykańskie ma wpływ na WIG.


Ale nie dotarliśmy jeszcze głównej myśli, czyli relacji S&P 500 i WIG. Możemy pokusić się o stworzenie czegoś na kształt dwu-, a później 3-czynnikowego CAPM opisywanego w poprzednim artykule. Dołóżmy do modelu stopę z SP500. Jeśli przyjmiemy, że stopa procentowa jest stała w czasie, to możemy pominąć stopę wolną od ryzyka i po prostu przyjąć 2-czynnikowy CAPM w postaci:

Oczekiwana stopa WIG(t) = stała + Beta*Stopa_SP500 + beta(labor)*Stopa_zmian_PKB_USA(t) 

Otrzymałem następujące parametry (stała praktycznie wyniosła zero i jest nieistotna):

Oczekiwana stopa WIG(t) = 0.96*Stopa_SP500(t) + 2.58*Stopa_zmian_PKB_USA(t)

R^2 = 63,5%, R^2 adj. = 62%.

Wnioski są oczywiste. Jeśli WIG potraktujemy jak zwykłą, ale dużą spółkę w indeksie SP500, to otrzymujemy bardzo silną zależność 0,96 pomiędzy S&P 500 a WIG.

Przy usunięciu zmiennej PKB, beta = 1,04, a zatem WIG będzie nieco silniej się odchylał niż SP500, ale R^2 jest wtedy niższy.

I na koniec można się zastanowić nad 3-cim czynnikiem. Ogólnie nasz CAPM wyglądał tak:

Uważny Czytelnik dostrzeże, że nasza regresja nie jest to CAPM, bo tam beta była zmienną, a stałe współczynniki były wyliczane z regresji. U nas jest odwrotnie: betę sobie wyliczyliśmy jako stałą. Z tego powodu nie mamy prawa twierdzić, że modelujemy zmienność bety. Jak już moglibyśmy się pokusić o stwierdzenie, że modelujemy zmienność oczekiwanej stop zwrotu SP500. Ponieważ definicja bety(prem) była następująca:

to w naszym przypadku ta beta(prem) zostanie obliczona na podstawie Metody Najmniejszych Kwadratów, która stosuje ten sam wzór. Musimy tylko dobrać odpowiednie zmienne. Zmiennymi pierwotnymi były Ri(t) - stopa zwrotu i-tego aktywa oraz R(prem)(t-1) - premia za ryzyko rynkowe z okresu t-1. Jednak, jak już wcześniej założyliśmy, stopa wolna od ryzyka będzie stała, a zatem premia za ryzyko może być wyrażona po prostu oczekiwaną stopą SP500. Ponieważ naszym celem jest odszukanie zmienności oczekiwanej stopy zwrotu SP500 albo, mówiąc bardziej ekonomicznie, cykliczności rynkowej, za R(prem)(t-1) podstawimy R(prem)(t-4), nazwijmy ją beta(2), czyli w naszym przypadku stopę zwrotu z SP500 sprzed 4 kwartałów. Mówiąc krótko, dostaniemy model:

Oczekiwana stopa WIG(t) = stała + Beta(1)*Stopa_SP500 + Beta(2)*Stopa_SP500(t-4) + Beta(3)*Stopa_zmian_PKB_USA(t)

Otrzymałem następujący model empiryczny ze wszystkimi istotnymi parametrami:

Oczekiwana stopa WIG(t) = 0.93*Stopa_SP500 - 0.28*Stopa_SP500(t-4) + 3*Stopa_zmian_PKB_USA(t)

R^2 = 66.7%, R^2adj. = 64.4%  - wysokie wartości wskazują na najlepsze dopasowanie z dotychczasowych modeli.

Poniżej dopasowanie obserwacji do analizowanego modelu przedstawia rysunek:

Model sugeruje, że stopa zwrotu SP500 sprzed 4 kwartałów, czyli 1 roku, wpływa ujemnie na bieżącą stopę WIG o ok. 30%. Jeśli wiemy, że rok temu SP500 urósł w 1 kw. o 10%, to możemy się spodziewać, że w tym roku w 1 kw. WIG spadnie o niecałe 3%, przy innych czynnikach niezmienionych. Można powiedzieć, że po roku następuje pewna zmiana w cyklu WIG. Co ciekawe, taka zależność nie występuje dla SP 500. Indeks amerykański nie reaguje na to co się działo na nim rok temu, z punktu widzenia regresji liniowej. 

Z czego może wynikać ta różnica? Moja hipoteza jest taka, że cykl gospodarczy w USA nie pokrywa się z cyklem gospodarczym w Polsce, a to powoduje, że WIG reaguje na przeszłe zmiany samego SP500 inaczej. Na przykład załóżmy, że cykl gospodarczy trwa w Polsce krócej niż w USA. To będzie powodowało, że WIG zacznie szybciej zmieniać kierunek, bo już po roku. W tym czasie w USA cykl jeszcze trwa. Jeżeli w USA cykl trwa dłużej, to pewna odwrotna reakcja na przeszłe zmiany powinna nastąpić po dłuższym okresie. Pytanie po jakim okresie? Z moich prób wynika, że po 7 kwartałach.
Kiedy zastosowałem model:

oczekiwana stopa zwrotu SP500 = stała + beta*stopa_SP500(t-7)

a więc sprawdziłem jak się zachowuje indeks po 7 kwartałach, to okazało się, że dostałem parametry istotne statystycznie:

oczekiwana stopa zwrotu SP500 = 0.02 - 0.25*stopa_SP500(t-7)

R^2 jest wprawdzie bardzo niski, bo tylko 8%, jednak nie ma wątpliwości, że istnieje ujemna zależność. 

Przedstawiona hipoteza byłaby fałszywa, gdyby WIG również miał istotne parametry i podobny R^2 dla identycznego modelu, tj dla

oczekiwana stopa zwrotu WIG = stała + beta*stopa_SP500(t-7)

Jednak w tym przypadku otrzymany parametr, za wyjątkiem stałej, jest nieistotny statystycznie (p = 0.34), zaś R^2 wynosi tylko 2,1%.

  Z powyższego można wnioskować, że rzeczywiście cykl SP500 jest dłuższy niż cykl WIG ok. 3 kwartały. To prawdopodobnie jest przyczyna, dla której Autor rzeczonego artykułu stwierdził, że bessa w USA nie zwiastuje bessy w Polsce. Cykle obu indeksów się nie pokrywają, cykle obydwu gospodarek mają prawdopodobnie różną średnią długość, lecz reakcja WIG na S&P 500 jest silna i dodatnia.


Źródło:

1. http://gieldowyracjonalista.blogspot.com/2013/11/czy-troj-betowy-capm-wyjasnia-stopy.html
2. http://10-procent-rocznie.blogspot.com/2014/02/czy-bessa-w-usa-udzieli-sie-polsce.html
3. http://www.gurufocus.com/stock-market-valuations.php
3. http://www.bea.gov/
4. stooq.pl