1) Kierunek, nie wartość.
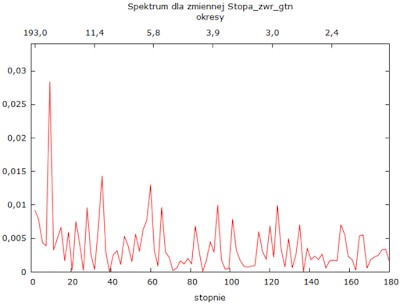
Chociaż w pracy Gómeza [1] czytamy, że FB może zostać przedstawiony jako najlepszy liniowy estymator z punktu widzenia średniokwadratowego błędu odchyleń, to jednak nie będzie tak w każdym przypadku. Sprawdziłem jak się zachowa FB dla funkcji sinus z nałożonym błądzeniem przypadkowym (300 danych). Analiza spektralna jednoznacznie wskazuje jedną powtarzającą się częstotliwość (o maksymalnym spektrum), która w stopniach wyniosła 12:
Po wstawieniu częstości odcięcia, x_c = 12, dostałem dość spodziewany efekt w postaci regularnej sinusoidy:
Jednak, jak się przyjrzeć dokładniej, nie jest to filtr, który minimalizuje błędy odchyleń. Np. jeśli wstawimy x_c = 20, otrzymamy lepsze dopasowanie:
Czyli FB (w powiązaniu z analizą spektralną) służy głównie do prognozowania kierunku, a mniej samej wartości.
2) Częstość odcięcia stopniowo tłumi wyższe od niej częstości.
Dlaczego gdy x_c = 20, nie pojawiają się jeszcze szumy na powyższym rysunku, skoro max spektrum zostaje osiągnięte dla x_c = 12?
Wiadomo, że przy dużo wyższych wartościach x_c, szumy się uwydatniają. Wstawmy x_c = 70:
A teraz x_c = 6. Tym razem filtr staje się płaski:
Zauważmy, że dla tego ostatniego częstości cyklu nie zostały usunięte, a przecież z periodogramu wynikałoby, że powinny. Ale okazuje się, że to już jest granica, bo dla x_c = 5, dostaniemy:
Dla x_c = 4, będzie to już prawie linia płaska.
Przeanalizujmy jeszcze przykład z nakładającymi się funkcjami sinus o różnej częstości i zmianami losowymi:
Spektrum:
3 piki o x_c = 2, 17 i 172 stopni.
Dla x_c = 2:
Dla x_c = 17:
Dla x_c = 172:
Łatwo się domyślić co będzie dla wartości pomiędzy 2 a 17, np. 9:
Źródło: Pollock, D. S. G. [3]
Oś pozioma to częstości x. Oś pionowa - wartości tzw. wzmocnienia filtru (gain of filter; filter gain). Rysunek przedstawia funkcję wzmocnienia filtra Butterwortha, G(x). Z matematycznego punktu widzenia wzmocnienie to po prostu współczynnik regresji, której zmienną niezależną jest np. sinus + szum, a zmienną zależną sam sinus, tj. filtr. Ten współczynnik nie jest jednak stałą, ale funkcją zależną od częstości x. Podobnie zmienna niezależna jest funkcją częstości x. Możemy w skrócie zapisać:
sygnał wyjściowy(x) = G(x) * sygnał wejściowy(x).
FB charakteryzuje się tym, że dla częstości x_c wzmocnienie zawsze wyniesie 0,5. Pokazano to na rysunku, gdzie za x_c podstawiono (pi/2 + pi/4) / 2. Czyli dla tej wartości G(x) = 0,5 czy po prostu G(x_c) = 0,5. Możemy więc w skrócie napisać:
FB(x_c) = 0,5 * sygnał wejściowy(x_c).
Czyli FB tłumi połowę sygnału wejściowego dla x_c, przez co wykres jest spłaszczony. I nie ucina natychmiast wszystkich częstości powyżej x_c, ale wraz z ich wzrostem coraz mocniej usuwa dane szeregu czasowego aż do zera.
Patrząc na rysunek widać, że x_c wyznacza środek procesu tego tłumienia (wyżej opisane G(x) = 0,5), jednakże nie wpływa na samą szybkość tłumienia. O tej szybkości decyduje drugi parametr FB, n. W zależności od jego ustawienia wykres G(x) staje się mniej lub bardziej nachylony i to właśnie wokół x_c (czyli ogólnie wzmocnienie zależy od dwóch parametrów i można byłoby zapisać G(x, n)). To dlatego jeden wykres jest zakreskowany i bardziej nachylony, a drugi (ciągły) bardziej prosty. Im bardziej prosty, tym częstości powyżej x_c zostaną szybciej stłumione.
Ten drugi parametr, o którym mowa, ustawialiśmy zawsze na poziomie n=2, aby uzyskać wersję filtru Hodricka-Prescotta. Co się stanie, gdy dla ostatniego przykładu podniesiemy go do 8, a x_c zachowamy na poziomie 9? Oto wynik:
A więc rzeczywiście częstości powyżej x_c = 9, zostały natychmiast stłumione, tak że te częstości drugiego rzędu zniknęły. Żeby się pojawiły, musielibyśmy zwiększyć x_c do 15.
Czyli żeby tłumienie zostało maksymalnie przyspieszone, musielibyśmy zmaksymalizować parametr n, tj. odejść od filtru Hodricka Prescotta. Jednak z punktu widzenia prognostyka jest to nie tylko niepotrzebne, ale i błędne rozwiązanie. Stopniowe tłumienie jest całkowicie wystarczające, a podwyższanie n prowadzi często do nieprawidłowych estymacji w przypadku rzeczywistych danych statystycznych.
Dodatek matematyczny:
Mamy sygnał wejściowy o losowym charakterze:
gdzie:
A - stała,
x - losowa częstość z przedziału (0, 2*pi),
t - czas.
Filtr jako odpowiedź na sygnał będzie funkcją:

gdzie:
G(x) - wzmocnienie albo tłumienie filtra,
P(x) - przesunięcie fazy.
Przesunięcie fazy, P(x), nie ma dla nas praktycznego znaczenia, bo dotyczy ono opisu fizycznych zjawisk, jak np. echo, które stanowi opóźnioną odpowiedź na sygnał wejściowy. Wobec tego dla nas P(x) = 0:
Tak więc wzmocnienie, o którym była mowa w artykule, stanowi współczynnik regresji.
Można pokazać [2], że:
gdzie:
g_F - gęstość spektralna dla F (funkcja gęstości spektralnej dla F),
g_S - gęstość spektralna dla S (funkcja gęstości spektralnej dla S).
Gęstość spektralna ma zbliżoną interpretację do autokorelacji pomiędzy obserwacjami, które występują z tą samą częstotliwością
Ogólnie wzór na gęstość spektralną jest postaci:
gdzie ACF_k oznacza autokorelację pomiędzy kolejnymi k-tymi (tj. w kolejnych k-tych jednostkach czasu) sygnałami o częstości x.
Dla wybranych częstotliwości (x) gęstości spektralne S i F będą się oczywiście nakładać. W tych miejscach g_F(x) = g_S(x), a wtedy:
Dla tych punktów G(x)^2 to po prostu współczynnik determinacji, a więc G(x) okazuje się także współczynnikiem korelacji między sygnałem wejściowym a filtrem.
Literatura:
[1] Gómez, V., The Use of Butterworth Filters for Trend and Cycle Estimation in Economic Time Series, Jul., 2001;
[2] Jenkins, G. M., General Considerations in the Analysis of Spectra, May, 1961;
[3] Pollock, D. S. G., Statistical Signal Extraction and Filtering: A partial survey, Aug. 2009.