Użycie filtru HP wymagało podanie jednego parametru - lambdy. Parametru tego używają inne filtry, w tym Butterwortha. Dla tego ostatniego Gómez [1] podaje wzór:
(1)
x_c - częstość cyklu podawana w radianach
n = 1, 2, 3, ... , gdzie większa wartość n generuje ostrzejszy filtr.
Gómez pokazuje, że dla n = 2,
(2)
Jak pamiętamy, Hodrick i Prescott sugerowali stosować lambdę równą 1600 dla danych kwartalnych. Rozwiązaniem równania (2) dla lambdy równej 1600, będzie x_c = 0,1583. Dla celów praktycznych musimy tę wartość przekształcić w stopnie. Maksymalną wartością x_c będzie zawsze pi, czyli 3,14, która oczywiście stanowi 180 stopni. Aby uzyskać 0,1583, należy podzielić 3,14 przez ok. 21. To znaczy, że 0,1583 w stopniach wynosi 180 / 21 = 8,6 stopni.
Zróbmy następujące ćwiczenie. W programie Gretl przeanalizujmy kwartalne zmiany PKB w cenach stałych (realny PKB), od 1 kw. 2003 do 3 kw. 2018 (częstość kwartalna). Najpierw tworzymy filtr HP, wybierając lambda = 1600. Dostajemy coś takiego:
Następnie wybieramy filtr Butterwortha (Zmienna -> filtracja -> Filtr Butterwortha). Za n wstawiamy 2, a za częstość odcięcia (w stopniach) 9. Wartość 9 wynika z zaokrąglenia 8,6, którą przed chwilą obliczyliśmy. Dostajemy wykres:
Identyczne, co dowodzi, że rzeczywiście dla tak ustalonych parametrów oba filtry się zazębiają. Jest to dobry punkt wyjścia do precyzyjniejszych prognoz.
Częstość x_c możemy oszacować na podstawie analizy spektralnej. Zanim to zrobimy, musimy sprawdzić czy szereg jest stacjonarny - jeśli nie, musimy go do takiego sprowadzić. W Gretlu są dostępne co najmniej 4 metody sprawdzania stacjonarności (resztę można pobrać w dodatkach). Zarówno KPSS jak i ADF jednoznacznie odrzucają niestacjonarność. Jednak, o dziwo, ADF-GLS i testy ułamkowego rzędu integracji nie pozwalają odrzucić hipotezy niestacjonarności. Spoglądając na wykres funkcji autokorelacji można dojść do wniosku, że winę za to odpowiada bardzo silna autokorelacja pierwszego rzędu (0,81) oraz silne autokorelacje drugiego (0,63) i trzeciego rzędu (0,42). Dalsze nie występują. Pamiętać należy jednak, że próbka zawiera zaledwie 63 obserwacje.
Zastosowanie analizy spektralnej do danych niestacjonarnych nawet graficznie nie pozwoli znaleźć długości cyklu, a zatem samą analizę spektralną możemy także wykorzystać do testowania stacjonarności. Otrzymałem taki periodogram:
Powstały obraz jest charakterystyczny dla szeregów niestacjonarnych. Dlatego wezmę pierwsze różnice zmian PKB, aby uzyskać stacjonarność. Wykres tych różnic to:
I wówczas periodogram tychże przedstawia się następująco:
Występują tutaj 3 piki sugerujące: cykl 16-kwartałowy (4 lata), 8-kwartałowy (2 lata) i 3-kwartałowy. Zajmiemy się tym pierwszym, najbardziej przekonującym.
To samo możemy uzyskać dużo szybciej, zmieniając po prostu w opcjach jednostki radianów na stopnie. Wchodzimy w Zmienna -> Periodogram - spektrum, i zmieniamy jednostki osi częstości z data-based na degrees:
Mając wiedzę o długości cyklu, skorzystamy z filtru Butterwortha, przy czym trzeba się zastanowić czy stosować go na oryginalnych zmianach PKB czy ich różnicach. Zróbmy zatem obydwoma sposobami. Najpierw na oryginalnych danych:
Dla danych niestacjonarnych istotnym elementem jest składnik cykliczny. W porównaniu do poprzedniego filtrowania, tym razem otrzymaliśmy informację, że cykl gospodarczy wszedł w fazę stagnacji (wartości składnika cyklicznego < 0).
Następnie zastosujmy filtr na danych stacjonarnych:
W tym przypadku nie zaznaczałem już składnika cyklicznego, bo jest on tu mniej przydatny - same dane są tu traktowane bardziej jako składnik cykliczny niż trend. Widzimy, że układa się dość równomierna sinusoida i obecnie faktycznie wchodzimy w fazę spadkową, co potwierdza analizę na trendzie. Całkiem rozsądne jest uznać, że użycie tych parametrów do filtru daje lepsze rezultaty dla danych de-trendowanych, stacjonarnych. W przypadku oryginalnego wykresu, prognoza będzie dużo mniej pewna, prowadzić będzie często do pozornych trendów i cykli.
W tym miejscu musi paść pytanie, dlaczego właściwie użyliśmy n = 2, czyli filtru HP, skoro właśnie chcemy dostać coś lepszego od HP? Przecież to jest ten sam filtr, tylko zgodnie ze wzorem (2) lambda wyniesie wtedy 43 (a nie 1600).
Możemy więc poeksperymentować. Skoro wiemy, że optimum x_c = 23, to możemy dostosować właściwe n. Tutaj za kryterium możemy przyjąć najmniejsze odchylenie standardowe składnika cyklicznego - a więc dla testów składnik cykliczny dla różnic okaże się jednak przydatny (bo traktujemy go nie jako składnik cykliczności, tylko jako błąd, odchylenie od tego składnika). W opcjach filtru Butterwortha zaznaczamy opcję "Zapisz składnik cykliczny jako" i kalibrujemy poziomem n, i przy każdej zmianie zmieniamy nazwę, np. dodając końcówkę 2, 3 itd. Dla n = 2, dostałem odch. standardowe = 0,87. Dla n = 3, wyniosło 0,88, a wykres samego składnika trendu wygląda tak:
Od n = 4 do n = 6, zmienia się postrzeganie bieżącej fazy cyklu - jest to faza wzrostowa. Jednak odchylenie standardowe ciągle rośnie. Dla n = 7 obecna faza znów staje się spadkowa, a odchylenie wzrasta do 0,98:
Skoro odchylenie ciągle rośnie, niezależnie od n, to optymalnym rozwiązaniem powinno być n = 2. A co z n = 1? Jest to niedopuszczalne rozwiązanie, co samemu łatwo sprawdzić.
Przykłady do giełdy:
Mając już pewną wiedzę na temat filtru Butterwortha, spróbujemy sporządzić prognozy dla WIG, sWIG80, AMC oraz GTN.
1) WIG: 1 kw 2003 - 4 kw 2018 (częstość kwartalna)
Periodogram dla stóp zwrotu:
Uzyskaliśmy bardzo wyraźną długość cyklu 13 kwartałów, tj. dokładnie 3 lata i 1 kwartał. Odpowiada to 27,7 stopni. W filtrze Butterwortha ustawimy n = 2 i x_c = 28. Wykres:
Filtr sugeruje, że jesteśmy niemal dokładnie w dołku filtra. Nie oznacza to zakończenia spadków, ale zakończenie dużych spadków (stopy zwrotu będą dążyć do zera).
2) sWIG80: 1 kw 2003 - 4 kw 2018 (częstość kwartalna)
Periodogram dla stóp zwrotu:
Dla mniejszego brata WIG-u uzyskaliśmy praktycznie to samo. Może dodatkowo uwidacznia się mniej wyraźny cykl 2,5 kwartałów (na wykresie odpowiada ok. 140 stopni).
W filtrze Butterwortha ustawimy n = 2 i x_c = 28. Wykres:
W tym przypadku faza bessy jest dużo bardziej drapieżna, co się da łatwo zauważyć na samych wykresach indeksów. Filtr wcale nie pozwala sądzić, że zbliżamy się do dołka. "Maluchy" łatwego życia nie mają (w ciągu ostatnich 5 lat sWIG80 spadł o 22%, WIG wzrósł o 20%). Należy jednak zaznaczyć, że ta słabość rynku małych spółek potwierdza tezę efektywności rynku, a zaprzecza tzw. efektowi małych spółek. Z drugiej strony to na sWIG80 występują najsilniejsze autokorelacje, które można będzie wykorzystać w odpowiednim czasie.
Przy okazji, gdy już jesteśmy przy autokorelacjach warto spojrzeć na tablice autokorelacji kwartalnych stóp zwrotu dla obu indeksów. Dla WIG:
Dla sWIG80:
Oprócz pierwszych dodatnich autokorelacji zwraca uwagę ujemna korelacja dla 7-go opóźnienia na ACF. To ona właśnie jest wykazywana jako faza odwrócenia w cyklu 2,5-kwartalnym. Prawdopodobnie ma to związek z efektami kalendarzowymi, gdy indeks lepiej zachowuje się np. od października do kwietnia i gorzej od maja do września.
Ponieważ już styczeń praktycznie minął, to dalej będę pracował na miesięcznych stopach zwrotu.
3) AMC: koniec grudnia 2002 - styczeń 2018 (częstość miesięczna):
Uwidacznia się na Amice cykl 39-miesięczny, tj. znów 3 lata i 1 kwartał. W filtrze Butterwortha ustawiamy n = 2 i x_c = 9. Rezultat poniżej:
Filtr wskazuje, że AMC wchodzi właśnie w fazę wzrostu. Jest więc szansa, że AMC wróci do sugerowanej przeze mnie wyceny 160-166 zł (CAPM skorygowany o PIT. Dalsza wycena Amiki). Tamta wycena opierała się na zbyt optymistycznych prognozach zysku operacyjnego w stosunku do rzeczywistości (nie tylko nie wzrósł, ale spadł o 7%), jednak niższa obecnie baza przyczyni się do łatwiejszego powrotu do średniego wzrostu.
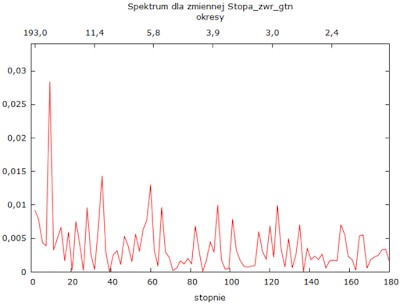
4) GTN: koniec grudnia 2002 - styczeń 2018 (częstość miesięczna):
Filtr Butterwortha (n = 2, x_c = 9):
Wygląda na to, że GTN nadal znajduje się w głębokiej depresji, chociaż końcówka sugeruje, że dołek coraz bliżej. Pewną nadzieją jest fakt, że stopy GTN są silnie skorelowane ze stopami WIG (wsp. kor. = 0,56), a WIG jest coraz bliżej dołka. Mimo to obecnie bardziej opłacalne wydaje się zainwestowanie w AMC, której korelacja w WIG jest trochę słabsza (0,48), a filtr daje właściwie sygnał kupna.
.........................................................................................................................
AKTUALIZACJA GTN:
Końcówka stycznia 2019 okazała się dla GTN wyjątkowo spektakularna. Kurs w ciągu zaledwie 4 dni, od 28.01.2019 do 31.01.2019, wzrósł o 46%. Spowodowało to, że charakter filtra zmienił się diametralnie w tym okresie:
.........................................................................................................................
W kontekście korelacji można zapytać czy skoro gospodarka wchodzi w fazę stagnacji, to warto inwestować w akcje? Tutaj przypomnę, że to WIG wyprzedza i prognozuje polskie PKB rok naprzód (zob. WIG dyskontuje prędzej Zagranicę niż Polskę), natomiast bieżące zmiany PKB mają słaby, możliwe, że nieistotny wpływ (korelacja roczna niecałe 0,17). PKB jednak się przyda, gdy będziemy przewidywać kolejny rok, bo indeks zareaguje w tym samym kierunku w roku bieżącym. Jeśli spojrzymy na obecne poziomy C/Z i C/WK WIG-u, które wynoszą na chwilę obecną odpowiednio 10,2 i 1, to stwierdzimy, że potencjał spadku jest jeszcze spory. Jeżeli już decydujemy się na akcje, to powinniśmy wybrać te, które wcześniej już drastycznie spadły, kiedy WIG jeszcze rósł.
W następnym artykule opiszę dokładniej co oznacza częstość odcięcia, dzięki czemu będziemy sprawniej używać filtra.
Literatura:
[1] Gómez, V., The Use of Butterworth Filters for Trend and Cycle Estimation in Economic Time Series, Jul., 2001.