Uogólniony wskaźnik Sharpe'a

W każdym podręczniku poruszającym temat zarządzania portfelem inwestycyjnym znajdziemy pojęcie wskaźnika Sharpe'a (SR - Sharpe Ratio). W procesie zarządzania podstawową kwestią jest zbadanie oczekiwanej (średniej) stopy zwrotu (u(Rp)) w stosunku do ponoszonego ryzyka. Tradycyjnie ryzyko określane jest przez odchylenie standardowe stopy zwrotu. W nawiązaniu do CAPM przyjęło się dodatkowo, żeby od oczekiwanej stopy zwrotu odjąć stopę wolną od ryzyka (R(f)), bo wtedy dostaniemy premię za ryzyko. Zatem SR ma postać:

Oczywiście im większy SR, tym lepsza jakość zarządzania portfelem.

Jest to znany i powszechnie stosowany miernik. Jednakże opiera się on na założeniu, że istnieją tylko dwa parametry rozkładu gęstości stopy zwrotu: średnia i wariancja. Założenie to ma teoretyczne podstawy, gdyż  zgodnie z Centralnym Twierdzeniem Granicznym średnia stopa zwrotu będzie dążyła do rozkładu normalnego, jeśli kolejne stopy zwrotu będą od siebie niezależne oraz będą posiadać identyczny rozkład prawdopodobieństwa oraz skończoną wariancję. To znane twierdzenie zostało jednak bardzo mocno uogólnione. Okazuje się, że średnia będzie dążyć do rozkładu normalnego, nawet jeśli zmienne są od siebie zależne [3], a nawet wtedy, gdy ich rozkłady nie będą jednakowe [1]. Właściwie jedynym ograniczeniem jest, aby średnia i wariancja były skończone. Trzeba jednak pamiętać, że w tych przypadkach zbieganie do rozkładu Gaussa będzie dużo wolniejsze niż dla klasycznego przypadku. (Przyjemnie opisane "działanie" tego twierdzenia można obejrzeć tutaj )

Badania jednak wskazują, że stopy zwrotu daleko odbiegają od rozkładu normalnego. Dziać się tak może z dwóch powodów. Po pierwsze twierdzenie mówi, że średnia stopa zwrotu dąży do r. Gaussa, a nie sama stopa (aczkolwiek zamiast średniej może być to po prostu suma, a więc logarytmiczna stopa zwrotu już mogłaby dążyć rozkładu normalnego). Po drugie wariancja może wbrew intuicji być nieskończona; co więcej wiadomo, że w wielu przypadkach tak właśnie się dzieje.

Nawet jeśli Centralne Twierdzenie Graniczne nadal obowiązuje na rynku, to prawdopodobnie potrzeba (bardzo) dużej próbki, aby testy potwierdzały normalność stóp zwrotu. Inwestor zarządzający portfelem nie może zatem lekceważyć pozostałych parametrów takich jak skośność i kurtoza.
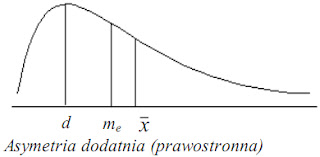
Skośność może być prawostronna lub lewostronna. Poniżej przykład skośności prawostronnej:

Ponieważ mediana, me, dzieli badaną strukturę na dwie równe części, a  średnia jest większa od mediany, to mniej niż połowa danych ma wartości większe od średniej.


A poniżej przykład lewostronnej:



Ponieważ mediana dzieli badaną strukturę na dwie równe części, a  średnia jest mnijesza od mediany, to ponad połowa danych ma wartości większe od średniej.

Kurtoza może być leptokurtyczna lub platykurtyczna. Poniżej widzimy  różne kształty rozkładu w porównaniu do rozkładu normalnego.

Leptokurtoza jest to kurtoza dodatnia i charakteryzuje się wysmukłym wierzchołkiem oraz tzw. grubymi ogonami, tj. rzadkie zdarzenia są częstsze niż dla rozkładu normalnego. Platykurtoza jest to kurtoza ujemna i charakteryzuje się spłaszczonym wierzchołkiem oraz cienkimi ogonami, tzn. mniej prawdopodobne zdarzenia są rzadsze niż dla rozkładu normalnego. 


 V. Zakamouline i S. Koekebakker [6] wyprowadzili SR uwzględniający skośność (ASSR - Adjusted for Skewness Sharpe Ratio). Wzór na ASSR jest następujący:

gdzie

χ - skośność rozkładu stopy zwrotu

b(3) - względna awersja do ryzyka.

Parametr b(3) jest ściśle związany z awersją do ryzyka Pratta-Arrowa. Przypomnę teraz, że w artykule Rozbieżność opinii w kontekście CAPM  zdefiniowana była awersja do ryzyka Pratta Arrowa następująco:

gdzie U - funkcja użyteczności inwestora (dopowiedzmy, że jeżeli awersja do ryzyka pozostaje wielkością stałą, to U jest dana wzorem: U(W) = y1 + y2*(-exp(-a*W)), dla a > 0, gdzie y1 to dowolna liczba; y2 > 0; W to inwestowana kwota. Zob. [5]).

Z kolei parametr b(n) jest dany wzorem:

gdzie n - liczba parametrów rozkładu stopy zwrotu.

Jeśli n = 2, wtedy stopa zwrotu jest opisana tylko wartością oczekiwaną i wariancją. Wtedy też b = 1.
W przypadku 3 parametrów, pojawia się skośność. Dostajemy wtedy wzór:

Parametr b(3) oznacza w tym wypadku preferencję w stosunku ryzyka skośności. Skośność wyznacza pewną osobliwą miarę ryzyka, którą za chwilę omówię. 
Na razie zauważmy, że ASSR zależy od preferencji inwestora, a nie tylko od własności stopy zwrotu. Co to oznacza? Że inwestorzy z różną preferencją do ryzyka skośności będą inaczej rangować ryzykowne aktywa.

Zauważmy teraz, że im większa (dodatnia) skośność, tym większy ASSR. Czyli lepsze zarządzanie portfelem, pomimo iż oczekiwana stopa zwrotu nie rośnie. Dzieje się tak, ponieważ większa dodatnia skośność znacznie zmniejsza ryzyko ujemnych stóp zwrotu i zwiększa prawdopodobieństwo bardzo dużych stóp zwrotu. Przypatrzmy się jednak obu obrazkom gdzie jest dodatnia skośność. Prawdopodobieństwo niskich stóp zwrotu zwiększa się, czyli jest to negatywny efekt, jednakże jest on równoważony przez spadek ujemnych stóp zwrotu i wzrost bardzo dużych stóp zwrotu. Oczekiwana stopa zwrotu pozostaje niezmienna, a jedynie częstości się przesuwają.

Odwrotna sytuacja występuje dla ujemnej skośności. Spada gwałtownie do zera szansa na bardzo duże zyski, rośnie szansa na umiarkowane zyski oraz rośnie szansa na straty. Z punktu widzenia ryzyka ujemna skośność jest niepożądana przez inwestora.

Od razu powiem, że nie jest to wcale proste do zrozumienia. Jeśli ujemna skośność rośnie coraz bardziej, to przecież rośnie szansa na przyzwoite zyski. Dlaczego więc to jest negatywne? Rzecz dotyczy tego samego aspektu co w przypadku innej miary ryzyka, Value at Risk, która mierzy tylko maksymalną stratę z danym prawdopodobieństwem. Trzeba pamiętać, że oczekiwany zysk się nie zmienia i choć największa szansa jest, że "będzie dobrze", to równocześnie rośnie niebezpieczeństwo, że "będzie źle" albo "bardzo źle".

Jednak faktyczna moc ASSR polega na tym, że jeśli inwestor nie ma w ogóle awersji do takiego ryzyka, to b = 0 i wtedy ASSR sprowadza się do SR. Pytanie czy jest to zasadne skoro VaR rośnie (maksymalna strata wzrasta ze względu grubszy lewy ogon rozkładu). Wątpliwe. Skąd jednak mamy wiedzieć jaką awersję do ryzyka skośności przyjąć?

Przy założeniu, że rozkład stopy zwrotu jest tzw. normalnym odwrotnym Gaussowskim rozkładem (nie jest to sztuczne założenie, tzn. ma również podstawy teoretyczne; rozkład ten jest jednym z uogólnień rozkładu normalnego. Co więcej, badania dowodzą, że doskonale dopasowuje się on do rozkładu dziennych stóp zwrotu [2])  U. Homm i C. Pigorsch [4] wyprowadzają uogólniony wskaźnik Sharpe'a (GSR - Generalized Sharpe Ratio), który nie zależy w ogóle od awersji do ryzyka. Wzór na GSR  jest następujący:

gdzie K - kurtoza albo precyzyjniej nadwyżka kurtozy, bo aby porównywać rozkład zmiennej z rozkładem normalnym, musimy odjąć od kurtozy liczbę 3.

Gdy skośność i K są równe 0, GSR sprowadza się do SR.

Jak widać powyższy wzór na GSR uwzględnia nie tylko skośność, ale dodatkowo także kurtozę, a więc ryzyko rzadkich zdarzeń, jak np. krach. Zatem kurtoza mierzy dodatkowo ryzyko załamania. Będzie tak, gdy K > 0. Oczywiście, jeśli K < 0, to ryzyko rzadkich zdarzeń staje się mniejsze niż dla rozkładu Gaussa, zatem ma wtedy pozytywny wpływ na GSR.

Wzór GSR może się wydać skomplikowany, ale jest łatwy w użyciu. Wystarczy podstawić, używając Excela, który ma wszystkie potrzebne miary statystyczne. Zwrócę tu uwagę, że Excel w swoich funkcjach nazywa nadwyżkę kurtozy właśnie kurtozą, a więc wystarczy wstawić bezpośrednią funkcję do wzoru.

Przykład.

Porównajmy SR i GSR na przykładzie paru wybranych spółek i WIG w okresie 30.11.2004 - 27.08.2013. Zakładając, że w tym okresie trzymamy pewne spółki i ich nie sprzedajemy, mierzymy co miesiąc stopę zwrotu (dywidendy są uwzględnione). Dane pobrałem ze stooq.pl. Czyli miesięczne stopy zwrotu stają się podstawą do wyznaczenia SR i GSR:

WIG:
SR = 12,8%.
GSR = 12,5%.

GSR jest mniejszy od SR z powodu ujemnej skośności (-0,37) oraz leptokurtozy (1,58).

PKO:
SR = 12,7%
GSR = 12,4%

SR i GSR dla PKO są niemal identyczne jak dla WIG.

PGD:
SR = 9,3%
GSR = 10,2%

GSR pokazuje, że w rzeczywistości premia za ryzyko w stosunku do podejmowanego ryzyka Pageda jest wyższa o 1% niż wskazywałby SR. Pomimo tej poprawy trzymanie tej spółki od końca 2004 r. do dziś wydaje się być złym pomysłem, skoro WIG przynosi wyższe wynagrodzenie w stosunku do ryzyka. 


LBW:
SR = 14,1%
GSR = 15,6%

W przypadku Lubawy sytuacja wygląda odwrotnie. Nie dość, że SR jest znacznie wyższe od WIG, to jeszcze GSR informuje, że ryzyko jest jeszcze mniejsze. Poprawa GSR wynika z dużej dodatniej skośności LBW, która zmniejsza ryzyko (dla WIG skośność była ujemna).

ELZ

SR = 15,1%
GSR = 15,9%.

Sytuacja Elzabu jest podobna jak w przypadku LBW, a więc znacznie pokonuje indeks.
Tym razem możemy dodatkowo porównać efektywność inwestowania w LBW z ELZ. Gdybyśmy je ocenili w oparciu o SR, to stwierdzilibyśmy, że trzymanie ELZ jest efektywniejsze niż LBW. Ale jak ocenimy je przez pryzmat GSR, to dowiadujemy się, że obie mają porównywalną efektywność: 15,9% u ELZ jest nieznacznie wyższe od 15,6% u LBW, intuicyjnie można wręcz powiedzieć, że różnica jest zaniedbywalna. Zatem jakość zarządzania portfelem w obu przypadkach jest praktycznie identyczna, pomimo że SR mówiłby co innego.

Literatura:

[1] Andrews D. W. K., An  Empirical  Process  Central  Limit  Theorem for  Dependent  Non-identically  Distributed Random  Variable,  Journal of Multivariate Analysis 38, 187-203 (1991);

[2] Barndorff-Nielsen, O.E., Normal Inverse Gaussian Distributions and Stochastic Volatility Modelling, Scandinavian Journal of Statistics, Volume 24, Issue 1, pages 1–13, March 1997;
[3] Hoeffding, W., Robbins H., The central limit theorem for dependent random variables,
Volume 15, Number 3 (1948), 773-780;

[4] Homm, U., Pigorsch, C., Beyond the Sharpe ratio: An application of the Aumann-Serrano index to performance measurement, April 7, 2012,
[5] Pratt, J. W., Risk Aversion in the Small and in the Large, Econometrica, Vol. 32, No. 1/2. (Jan. - Apr., 1964), pp. 122-136;
[6] Zakamouline, V. ; Koekebakker, S., Portfolio performance evaluation with generalized Sharpe ratios: Beyond the mean and variance, Journal of Banking & Finance, 22 August 2008.

Źródło danych statystycznych: stooq.pl.