Pytanie, które z pewnością nie jeden inwestor zadawał, jest następujące. Jeżeli giełdowe stopy zwrotu zależą od różnych czynników ekonomicznych, takich jak cykl gospodarczy, inflacja, stopy procentowe oraz czynników psychologicznych takich jak wysokie lub niskie oczekiwania co do przyszłych zmian wyników finansowych, to w czy w takim razie są one zjawiskiem dynamicznym, nie posiadającym stałego rozkładu prawdopodobieństwa? Czy parametry rozkładu, takie jak wartość oczekiwana i wariancja (a zapewne też skośność i kurtoza) zmieniają się w czasie? Jeśli zapytamy o to dowolnego inwestora czy spekulanta, który "coś tam słyszał, czytał" albo nawet kiedyś "miał na studiach" elementy ekonometrii, to każdy bez wyjątku (obiecuję to) powie, że rozkład jest dynamiczny. Dodatkowo stwierdzi, że rozważanie stosowalności modeli ekonometrycznych na giełdzie nie ma większego sensu, bo stopy zwrotu zmieniają swoją strukturę w czasie, a modele ekonometryczne są zbyt statyczne. Dostaniemy cały wykład na temat psychologii ludzi, która wymyka się statystyce (lub że będzie ona podlegać statystyce w zbyt długim okresie czasu, by móc to praktycznie wykorzystać) i że żadne twierdzenie matematyczne (odwołując się do prawa wielkich liczb lub centralnych twierdzeń granicznych) nie jest w stanie modelować ludzkich zachowań. Taką odpowiedź dostaniemy na 100%. Dlaczego? Bo ludzie sądzą, że są niezwykli i stąd ich zachowania nie mogą być badane tak jak zjawiska przyrodnicze.
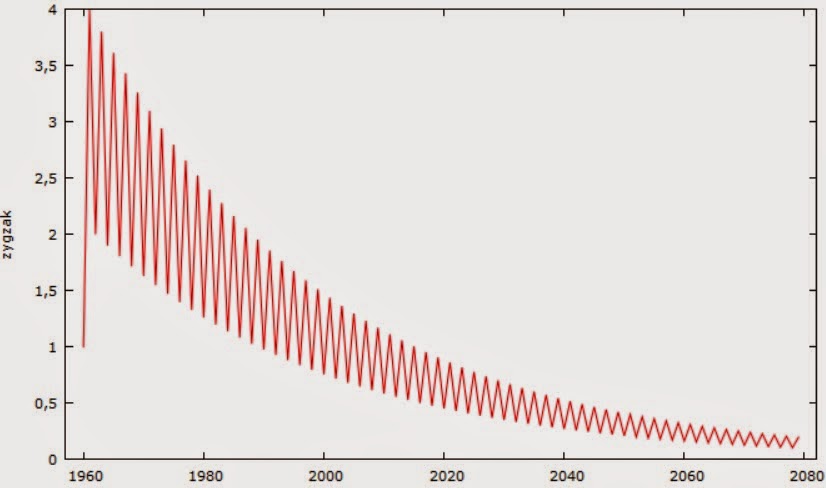
Ale każdą teorię, jeśli traktować poważnie, powinno potrafić się zweryfikować. Jak to sprawdzić? Oczywiście mamy tu do czynienia z hipotezą niestacjonarności stóp zwrotu. Powstało wiele testów na tę hipotezę, co więcej, metody są ciągle rozwijane i dyskutowane. W literaturze przedmiotu znajdujemy dwa podstawowe podejścia. Pierwsze rozwiązanie to sprawdzenie autokorelacji próbki kolejnych rzędów. Jest to po prostu korelacja pomiędzy obserwacją z bieżącego okresu a obserwacją z p-tego okresu jakiejś zmiennej. Jeśli funkcja autokorelacji dla każdego kolejnego p spada "powoli", to prawdopodobnie mamy do czynienia z niestacjonarnością [1, 2]. W ogólnym przypadku, czyli gdy rozkład nie musi być normalny, współczynnik autokorelacji Pearsona wychwytuje 2 czynniki: znaki pomiędzy kolejnymi obserwacjami oraz odległość pomiędzy kolejnymi obserwacjami. Nawet jeśli kolejne znaki są różne, to jeśli odległość pomiędzy kolejnymi danymi będzie (średnio) dodatnia, to współczynnik korelacji będzie dodatni. Np. przeanalizujmy taki wykres:
Rys. 1
Mogłoby się wydawać, że autokorelacja 1 rzędu będzie tu ujemna, ale faktycznie wynosi +0.56. Wynika to właśnie z tego, że średnio obserwacje oddalają się od siebie. Z punktu widzenia samego badania autokorelacji, jest to oczywista bzdura. W tym przypadku autokorelacja jest doskonale ujemna, czyli prawdziwy współczynnik korelacji powinien wynieść -1. Prawidłowy współczynnik autokorelacji nie powinien uwzględniać odległości pomiędzy kolejnymi obserwacjami, ale właśnie tylko znaki. O ile w korelacji między zmiennymi zależnymi odległości te mogą być przydatne (wskazując siłę zależności), o tyle w samej autokorelacji wypaczają jej sens.
To pokazuje tylko, że współczynnik autokorelacji Pearsona jest bardzo słabym miernikiem faktycznej autokorelacji, jeśli próba nie pochodzi ze stacjonarnej zmiennej. Ale z drugiej strony, taka właściwość współczynnika korelacji pozwala właśnie ocenić czy mamy do czynienia z niestacjonarnością. Poniższy wykres przedstawia współczynniki autokorelacji dla kolejnych opóźnień procesu z rys. 1. Niebieska linia reprezentuje próg istotności statystycznej. Widać, że korelacja spada powoli, co świadczy o niestacjonarności procesu.
Przykład zygzaka jest oczywisty, bo na oko widać, że to proces niestacjonarny. Wystawmy na próbę bardziej skomplikowane procesy. Co z periodycznymi lub quasi-periodycznymi ruchami, które stają się bliższe chaosowi deterministycznemu?
Weźmy taki przykład:
Rys. 2
Nie mamy raczej wątpliwości, że jest to proces niestacjonarny. Jak w takim przypadku zachowuje się ACF (Autocorrelation Function)? Znów dostajemy wysoką autokorelację, która z każdym opóźnieniem, czyli rzędem p, spada bardzo wolno:
Rys. 3
Powyższy przykład jest całkiem niezły, bo nie ma w nim konkretnego trendu, a mimo to narzędzie w postaci ACF daje bardzo solidne dowody, że proces jest niestacjonarny. Przecież niestacjonarność może nie mieć tak prostego oblicza
jak wyrazisty trend.
Niestety problem pojawia się w bardziej subtelnych danych, takich jak te z rys. 4:
Rys. 4
Miejscami wykres wydaje się wskazywać na niestacjonarność, jednak ogólnie jest to sytuacja tak rozmyta, że wszelkie dostrzegane wzory na tym wykresie można uznać za złudzenie. Co mówi korelogram?
Rys. 5
Sytuacja jest niepewna, bo korelacja najpierw dość szybko spada, ale nagle szybko się podnosi i utrzymuje się ponad progiem istotności. Przypomina nieco przykład zygzaka, który zmieniał gwałtownie korelację, ale tutaj ACF nie daje jednoznacznej odpowiedzi. Skłania nas do poszukiwania bardziej formalnego egzaminu.
D.A. Dickey z pomocą swojego promotora W.A. Fullera, napisał w 1976 r. dysertację, w której stworzył test na niestacjonarność procesu, dziś nazywany testem Dickeya-Fullera (DF) [2]. W 1979 r. obaj napisali artykuł, w którym opublikowali rozszerzony test, tzw. Augmented Dickey-Fuller test (ADF) [3]. Różnica polega na tym, że w DF błąd statystyczny modelu jest zawsze białym szumem, a w ADF nie musi być, czyli może np. zawierać autokorelacje [1]. W 1991 r. Kwiatkowski et. al., stwierdzili, że ADF zawodzi w niektórych danych ekonomicznych, błędnie odrzucając hipotezę niestacjonarności. Skonstruowali test, znany dziś pod skrótem KPSS (Kwiatkowski, Phillips, Schmidt, Shin). odwrotny niż ADF, bo w ADF hipotezą zerową jest niestacjonarność, a w KPSS stacjonarność [4].
Testy na niestacjonarność są stosunkowo nowe, ale zarówno ADF jak i KPSS uznawane są dziś jako standard w narzędziach ekonometrii. Dostępne są np. w Gretlu. Sprawdźmy więc jak te narzędzia sobie radzą.
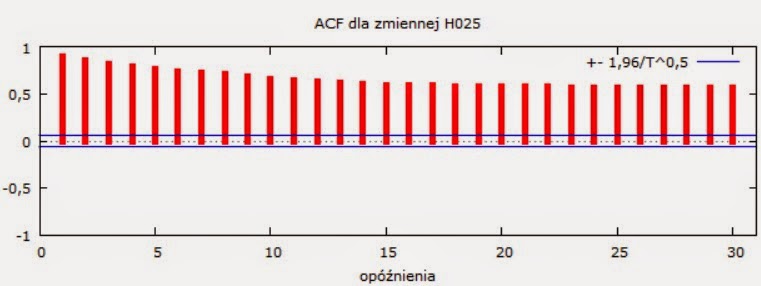
Model ADF dla szeregu z rys. 2:
Dostajemy takie oto statystyki ADF (wchodzimy w Zmienna -> Testy pierwiastka jednostkowego -> Test ADF):
Rozszerzony test Dickeya-Fullera dla procesu H025
dla opóźnienia rzędu 18 procesu (1-L)H025
(maksymalne było 21, kryterium zmodyfikowane AIC)
liczebność próby 1005
Hipoteza zerowa: występuje pierwiastek jednostkowy a = 1; proces I(1)
test z wyrazem wolnym (const)
model: (1-L)y = b0 + (a-1)*y(-1) + ... + e
Autokorelacja reszt rzędu pierwszego: -0,001
opóźnione różnice: F(18, 985) = 6,096 [0,0000]
estymowana wartość (a-1) wynosi: -0,0364048
Statystyka testu: tau_c(1) = -2,38399
asymptotyczna wartość p = 0,1463
Bardzo ważna jest tu hipoteza zerowa, która brzmi, że występuje pierwiastek jednostkowy a = 1; proces I(1).
Chociaż żeby dobrze zrozumieć, dlaczego pierwiastek jednostkowy jest tu utożsamiany z parametrem a, musielibyśmy przestudiować zagadnienia matematyczne, to dla naszych potrzeb wystarczy na razie wiedzieć, że pierwiastek jednostkowy musi być kojarzony z niestacjonarnością.
Wartość p = 0,146 > 0,05, a więc możliwy błąd odrzucenia hipotezy zerowej wynosi 0,146. Ogólnie nie możemy odrzucić hipotezy zerowej, co oznacza, że przyjmujemy niestacjonarność badanego procesu.
Model KPSS dla szeregu z rys. 2:
Następnie dla szerszej perspektywy, robimy test KPSS (wchodzimy w Zmienna -> Testy pierwiastka jednostkowego -> Test KPSS). Dostajemy następujące statystyki:
Hipoteza zerowa: proces stacjonarny.
Test KPSS dla zmiennej H025
T = 1024
Parametr rzędu opóźnienia (lag truncation) = 7
Statystyka testu = 1,59819
10% 5% 1%
Krytyczna wart.: 0,348 0,462 0,743
wartość p < .01
W tym przypadku od razu Gretl nam podpowiada, że hipoteza zerowa to proces stacjonarny.
Aby znaleźć prawidłową odpowiedź, patrzymy najpierw na statystykę testu, która wynosi 1,598 i porównujemy ją z krytyczną wartością przy różnych poziomach istotności. Jeśli statystyka testu jest większa od krytycznej wartości, to odrzucamy hipotezę zerową. Standardowo głównie nas interesuje wartość krytyczna przy 5% istotności. Czyli 1,598 > 0,46, a zatem odrzucamy hipotezę zerową o stacjonarności procesu (z dużą większą pewnością niż ADF).
Zarówno ADF jak i KPSS dały tę samą odpowiedź, co oznacza, że nie mamy wątpliwości, iż szereg czasowy ma strukturę zmienną w czasie. Jednak to było dość oczywiste. Dużo bardziej interesujące będzie sprawdzenie rysunku nr 4.
Model ADF dla szeregu z rys. 4:
Rozszerzony test Dickeya-Fullera dla procesu H003
dla opóźnienia rzędu 20 procesu (1-L)H003
(maksymalne było 21, kryterium zmodyfikowane AIC)
liczebność próby 1003
Hipoteza zerowa: występuje pierwiastek jednostkowy a = 1; proces I(1)
test z wyrazem wolnym (const)
model: (1-L)y = b0 + (a-1)*y(-1) + ... + e
Autokorelacja reszt rzędu pierwszego: 0,000
opóźnione różnice: F(20, 981) = 3,350 [0,0000]
estymowana wartość (a-1) wynosi: -0,314178
Statystyka testu: tau_c(1) = -4,30171
asymptotyczna wartość p = 0,0004362
ADF wskazuje jednoznacznie, że proces jest stacjonarny, bo p = 0,0004 < 0,05
Model KPSS dla szeregu z rys nr 4:
Hipoteza zerowa: proces stacjonarny.
Test KPSS dla zmiennej H003
T = 1024
Parametr rzędu opóźnienia (lag truncation) = 7
Statystyka testu = 0,430991
10% 5% 1%
Krytyczna wart.: 0,348 0,462 0,743
Interpolowana wartość p 0,063
Statystyka testu = 0,43 < 0,46, a więc proces jest raczej stacjonarny. Trzeba jednak natychmiast zaznaczyć, że różnica jest bardzo niewielka, p = 0.063 > 0.05 świadczy o, że moglibyśmy przyjąć niestacjonarność. KPSS jest dużo bardziej wrażliwy i przez to lepszy od ADF, bo wskazuje, że stacjonarność jest trochę umowna.
Obydwa testy skłaniają ku tej samej odpowiedzi, przez co metoda korelogramu została wzmocniona. Przykład ten dobitnie pokazuje, że lepiej posługiwać się testami statystycznymi. Gdy mamy do czynienia z tak subtelnymi danymi jak stopy zwrotu na giełdzie, powinniśmy szczególnie mieć to na uwadze.
Możemy więc w końcu sprawdzić czy faktycznie giełda ma tak zmienną strukturę jak się powszechnie sądzi. Wszystkie dane pobrane zostały ze stooq.pl.
Zacznijmy od miesięcznych stóp zwrotu S&P 500 w latach 1940-2013 (dane ze stooq.pl), 882 obserwacje. Test ADF wskazuje na p = 0, zatem hipotezę o niestacjonarności należy odrzucić. Test KPSS daje następujące statystyki:
Statystyka testu = 0,04876
10% 5% 1%
Krytyczna wart.: 0,348 0,462 0,743
wartość p > .10
0,049 < 0,462 , czyli proces jest stacjonarny.
Przetestujmy teraz polską giełdę. Weźmy miesięczne stopy zwrotu mWIG40od początku notowań styczeń 1998-pażdziernik 2014; 198 obserwacji. Test ADF wskazuje na stacjonarność (p = 0). KPSS również wskazuje na stacjonarność (Statystyka testu = 0,0616738 < 0,348 przy 10% istotności).
Następnie weźmy tygodniowe stopy zwrotu mWIG40 w tym samym zakresie czasu; 878 obserwacji. ADF wskazuje na stacjonarność (p = 0), KPSS też na stacjonarność (Statystyka testu = 0,0789135 < 0.348 przy 10% istotności).
To samo zróbmy dla dziennych stóp zwrotu mWIG40, ale w okresie styczeń 2001-październik 2014; 3469 danych. Zarówno ADF jak i KPSS wskazują na stacjonarność (odpowiednio p = 0 dla ADF i 0,174 < 0,46 przy 5% istotności dla KPSS).
Zatem dla każdej częstości stopy zwrotu okazują się być procesem stacjonarnym z punktu widzenia klasycznej statystyki.
Przypatrzmy się jednak dziennym stopom zwrotu mWIG40 w testowanym okresie:
Rys. 6
Występuje tu zjawisko zwane grupowaniem wariancji: po serii dużych wariancji, następuje seria małych wariancji. Proces ten jest dobrze znany od dawna i w ekonometrii został rozwiązany przy pomocy modeli klasy ARCH. Modele te jednak w klasycznej formie są stacjonarne. Wynika to z faktu, że uwzględniają one warunkowe zmiany wariancji, tzn. takie zmiany, które następują pod wpływem zmian z przeszłości. Nawet jeśli wariancja warunkowa się zmienia, to wariancja niewarunkowa będzie w tych modelach stała.
I w tym miejscu rodzi się bardzo ważna nowa wskazówka. Okazuje się, że w rzeczywistości ADF i KPSS wcale nie wykrywają zmienności wariancji, tylko zmienność średniej. Jeśli weźmiemy taki oto przykład
to nie ma najmniejszych wątpliwości, że wariancja zmienia się w czasie, czyli proces jest niestacjonarny. Jednak średnia jest stała i wynosi 0. ADF wskazuje, że proces jest stacjonarny (p = 0), KPSS - tak samo (Statystyka testu = 0,032 < 0,46). Nie znaczy to, że wszystkie testy pierwiastka jednostkowego testują tylko średnią. Np. gdy te dane przetestowałem zmodyfikowanym testem ADF, zwanym ADF-GLS, dostałem niestacjonarność. Wtedy przyszło mi do głowy pytanie, jak w takim razie ADF-GLS oceni dzienne stopy zwrotu mWIG40 z rys. 6? Okazało się, że test kazał odrzucić hipotezę o niestacjonarnosci (p = 0,0001), a więc tak jak ADF i KPSS. Jest to mocny dowód na to, że wariancja niewarunkowa jest stała w czasie, tak jak to przewidują modele ARCH.
W ten sposób dokonałem praktycznego odkrycia, że ADF i KPSS mogą służyć do testowania stabilności średnich stóp zwrotu (przy czym KPSS wydaje się lepszy), natomiast ADF-GLS jest dobrym narzędziem do testowania stabilności wariancji niewarunkowej, czy ogólnej stacjonarności stóp zwrotu.
Powstaje jednak pytanie czy jeśli klasyczne testy na zmienność średniej w czasie stwierdzą, że nie ma tej zmienności, to czy rzeczywiście tak jest? Czy nie powinniśmy w dalszej kolejności użyć metod wykrywających chaos deterministyczny lub fraktalność? De facto chodzi nam o wykrycie ułamkowej niestacjonarności. W Gretlu razem z klasycznymi testami na niestacjonarność, znajdziemy także test na ułamkowy rząd integracji.
Mówiąc prosto, wiadomo że jeżeli proces jest niestacjonarny, jak np. cena akcji, to można doprowadzić go do stacjonarności poprzez odjęcie od ceny z t okresu ceny z t-1 okresu. Wtedy dostajemy proces zintegrowany 1 rzędu. Jednak taka transformacja może nie wystarczyć do doprowadzenia do stacjonarności, a to dlatego że cena akcji rośnie np. wykładniczo. Możliwe, że będzie konieczne ponowne zróżnicowanie, czyli ponowne wzięcie różnicy pomiędzy obserwacją (która jest różnicą cen) z t-tego okresu a obserwacją z t-1 okresu. Wtedy dostaniemy proces zintegrowany 2 rzędu. I tak można zwiększać ów rząd.
Widać, że kolejne rzędy są liczbami całkowitymi. Co jednak się stanie jeśli przyjęlibyśmy ułamkowy rząd, to znaczy, odjęlibyśmy tylko pewną część obserwacji z poprzedniego okresu? Dostaniemy wtedy proces zintegrowany ułamkowego rzędu. Skoro jednak odjęliśmy tylko pewną część procesu, to znaczy, że ta pozostała część może mieć ciągle wpływ na kolejną wartość. Np. jeśli testujemy stopy zwrotu i od stopy zwrotu z t-tego okresu odejmujemy tylko pewną część stopy zwrotu z okresu t-1. Pomiędzy stopami z różnych okresów może więc wystąpić pewna zależność. Zadaniem testu na ułamkowy rząd integracji jest znalezienie takiej zależności. Im większy ułamkowy rząd integracji, tym większa fraktalna zależność. Gdy równa się on 0, wtedy brak tej zależności i jednocześnie brak ułamkowej niestacjonarności. Okazuje się, że gdy jest większy od 0, ale mniejszy lub równy 1/2, to proces jest ułamkowo lub lokalnie stacjonarny (asymptotycznie stacjonarny) i jednocześnie posiada długą pamięć, a gdy jest większy od 1/2, staje się w pełni niestacjonarny.
W ten sposób ułamkowa autokorelacja wiąże się z ułamkową niestacjonarnością.
Gretl przeprowadza 2 testy na ułamkowy rząd integracji: Whittle'a oraz GPH (Geweke'a, Portera-Hudaka). Dla omawianych obserwacji dziennych stóp zwrotu mWIG40, dostałem następujące statystyki:
Estymator lokalny Whittle'a (m = 132)
Estymowany ułamkowy rząd integracji = 0,171471 (0,0435194)
Statystyka testu: z = 3,94011, z wartością p 0,0001
Test GPH (Geweke'a, Portera-Hudaka) (m = 132)
Estymowany ułamkowy rząd integracji = 0,175429 (0,0611883)
Statystyka testu: t(130) = 2,86704, z wartością p 0,0048
Hipoteza zerowa zakłada, że rząd integracji = 0 (czyli brak ułamkowych zależności i niestacjonarności). Jak widać w obu przypadkach p < 0,05 , czyli istnieje fraktalna zależność pomiędzy stopami zwrotu, co jednocześnie oznacza istnienie ułamkowej niestacjonarności. Powinienem także zwrócić uwagę, że dla procesu z rys. 4 ułamkowy rząd również występuje i wynosi odpowiednio dla testu Whittle'a i GPH 0,31 (p=0) i 0,27 (p=0.0029).
Warto też przypomnieć [5], że wykładnik Hursta jest ścisle zależny od ułamkowego rzędu integracji i jest dany wzorem:
H = d + 1/a
gdzie d - ułamkowy rząd integracji, a - parametr alpha rozkładu Levy'ego jako miara rozciągliwości rozkładu. Dla a = 2, dostajemy rozkład Gaussa. Estymacją Mccullocha obliczyłem, że dla testowanego szeregu dziennych stóp zwrotu mWIG40 a = 1,56. W przypadku takich skoków i zmian wariancji z rys. 6, nie można uzyskać a = 2, tj. rozkładu normalnego. W tym przypadku H = 0.17 + 1/1.56 = 0.81. Gdyby rozkład był normalny, ale z przedłużoną wariancją, wówczas H wyniósłby 0.67 (0.5 + 0.17).
Podsumowując, zmienność oczekiwanych stóp zwrotu może nie jest mitem, ale z pewnością nie jest również sprawą oczywistą. Klasyczne testy na niestacjonarność nie wykrywają tej zmienności (byłoby to chyba za proste) i tylko testy na ułamkowe autokorelacje stanowią swoisty dowód, że ma ona miejsce w postaci lokalnej niestacjonarności.
Literatura:
[1] Maddala, G.S., Introduction to Econometrics (Third Edition) , 2001,
[2] Dickey, D. A., Estimation and hypothesis testing in nonstationary time series, 1976,
[3] Dickey D.A.; Fuller W.A., Distribution of the Estimators for Autoregressive Time Series with a Unit Root, 1979,
[4] Kwiatkowski D., Phillips P.C.B, Schmidt P., Shin Y., Testing the null hypothesis of stationarity against the alternative of a unit root, 1991,
[5] http://gieldowyracjonalista.blogspot.com/2010/07/uamkowy-ruch-levyego-czyli-nic-nie-jest.html
P.S. Czytelnik może zauważyć dziwne nazwy testowanych przez Gretl procesów, jak H025 i H003. Nazwy te biorą się z natury wygenerowanych przez mnie procesów o różnych wykładnikach Hursta H. Pierwszy proces posiada H=0.25, drugi H=0.03. Dla rozkładu normalnego i H=0.5 dostalibyśmy proces ruchu Browna. Wynika z tego, że formalnie rzecz biorąc skomplikowany proces H=0.03 jest niestacjonarny, czyli KPSS słusznie "wahał się" w jego ocenie. Z moich obserwacji wynika, że KPSS jest dużo wrażliwszy i lepszy od ADF.