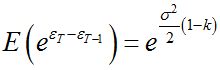Średnia warunkowa czy niewarunkowa?

Finansiści, stosując od czasu do czasu regresję liniową, np. model trendu, rzadko myślą o zmiennej losowej warunkowej. Ale to właśnie pojęcie warunkowości tworzy różnicę pomiędzy zwykłą średnią arytmetyczną a stopą w modelu trendu. Ostatnio pokazałem to za pomocą "Smarującego estymatora" (SE) Duana. SE posłużył mi jako oczekiwana stopa zwrotu w dwóch przypadkach:
1) gdy cena rośnie wykładniczo w czasie, tzn. prawdziwy jest model P(t) = e^(bt + składnik losowy), przy czym składnik losowy może pochodzić z dowolnego rozkładu;
2) gdy cena nie zależy od czasu, tzn. średnio znajduje się ciągle na tym samym poziomie. Np. WIG od końca 10.2006 do końca 10.2016 to praktycznie linia płaska:

Okazało się, że w tym drugim przypadku SE sprowadza się do niewarunkowej średniej arytmetycznej stopy zwrotu. Natomiast gdy istnieje wykładnicza zależność od czasu, to SE jest warunkową średnią równą e^b*D, gdzie D to korekta Duana liczona jako średnia arytmetyczna z wykładniczych składników losowych e^(składnik losowy). Zatem, jeżeli czas staje się warunkiem dla zmian kapitału, to średnia niewarunkowa przekształca się w średnią warunkową.

Jednak inwestor przyzwyczajony do pojęcia stopy zwrotu zaczyna się zastanawiać: w jaki sposób czas miałby w ogóle wpływać na stopę zwrotu? Przecież po to właśnie jest pojęcie stopy, czyli procentu, aby uniezależnić zmiany kapitału od kolejnych okresów. Ale gdy spojrzymy na to zagadnienie tak jak na różnicę pomiędzy średnią arytmetyczną a geometryczną, odpowiedź staje się jaśniejsza: gdy obliczamy średnią geometryczną, uwzględniamy fakt, że wartość kapitału zależy od okresu poprzedniego, bo jest jakby oprocentowany. Natomiast gdy wyznaczamy średnią arytmetyczną, każdą zmianę kapitału traktujemy całkowicie niezależnie od poprzednich okresów. To stąd przecież powstaje różnica pomiędzy "długookresową średnią stopą zwrotu" a "krótkookresową średnią stopą zwrotu", wskazując w pierwszym przypadku na czasową zależność zmian kapitału oraz w drugim przypadku na ich niezależność.

A stąd już tylko krok do zrozumienia różnicy pomiędzy warunkową a niewarunkową średnią: ta pierwsza zawiera część stochastyczną D oraz część systematyczną e^b. Część systematyczna jest niczym innym jak średnią geometryczną brutto w rozkładzie ciągłym. Oczywiście jest różnica między rozkładem ciągłym a dyskretnym, ale w modelu ciągłym zakładamy, że pomiędzy dwoma oddalonymi punktami możemy wstawić pewną średnią z tych punktów, ponieważ czas jest ciągły. Nie będzie to średnia arytmetyczna, ale właśnie geometryczna. Jeżeli mamy okres pomiędzy 10 a 11, np. 10,5 i chcemy wyznaczyć teoretycznie ten punkt, to zauważmy, że średnia geometryczna brutto z wartości pomiędzy okresem 10 a 11 równa się (e^10*e^11)^0,5 = e^(21*0,5) = e^10,5. Trzeba jednak zaznaczyć, że przejście od rozkładu dyskretnego do ciągłego w rzeczywistości wszystko zmienia, bo o ile w dyskretnym stopy brutto wewnątrz okresu się redukują, tak że wpływ na średnią ma jedynie pierwsza i ostatnia wartość, o tyle w ciągłym już tego zrobić nie mogą i jest to poniekąd przyczyna, dla której średnia geometryczna brutto w rozkładzie ciągłym staje się równa medianie, co odpowiada temu co napisałem kiedyś w Istota i znaczenie logarytmicznej stopy zwrotu.

Oczywiście trzeba pamiętać, że średnia warunkowa jest znacznie szerszym pojęciem niż tylko w kontekście czasu. Częściej średnia warunkowa traktowana jest w powiązaniu z inną zmienną losową. Np. w dwuwymiarowym rozkładzie normalnym, w którym zmienne losowe X i Y są ze sobą skorelowane, wartość oczekiwana Y pod warunkiem, że X = x jest dana wzorem [2]:

Jeżeli współczynnik korelacji ρ jest równy zero, warunkowa wartość oczekiwana Y sprowadza się do niewarunkowej wartości oczekiwanej m(Y). W przeciwnym razie Y zależy od zachowania X. Na przykład Y może być stopą zwrotu z akcji, a X stopą zwrotu z indeksu giełdowego. Gdyby obie pochodziły z rozkładu normalnego, to przedstawiona relacja byłaby zawsze prawdziwa i zawsze liniowa. Widać więc, jak istotną rolę pełni warunkowość, którą można rozpatrywać zarówno w kontekście przestrzeni jak i czasu.

Literatura:
[1] N. Duan, Smearing Estimate: A Nonparametric Retransformation Method, Sep. 1983,
[2] Z. Hellwig, Elementy rachunku prawdopodobieństwa i statystyki matematycznej, PWN W-wa 1998.

Smarujący estymator

Poprzednio pokazałem, że gdy przyjmiemy model geometrycznego procesu ruchu Browna (model ceny aktywa):

(1)

oraz wiedząc, że parametr b jest nieznany, tak że możemy jedynie oszacować jego wartość na podstawie próby losowej, to wartość oczekiwana stopy zwrotu (R) może być oszacowana za pomocą modelu:

(2)

gdzie b z falką to estymator MNK z modelu ln(P) = b*T + składnik losowy.

Wyraz k wyraża błąd retransformacji z postaci liniowej do nieliniowej (pierwotna jest postać nieliniowa, która jest transformowana do liniowej przez logarytmowanie, aby zastosować MNK; następnie powracamy do postaci nieliniowej, czyli dokonujemy retransformacji). Jak widać przy nieco większym T, wyraz k ma bardzo mały wpływ.

Geometryczny ruch Browna zakłada jednak rozkład log-normalny. Z tym rozkładem jest ten problem, że jego lewy ogon bardzo szybko zbiega do zera:

W rzeczywistości dobrze wiemy, że na giełdach zdarzają się rzadkie, ale bardzo silne odchylenia, a także asymetria. Kwartalny sWIG80 od 01.1994 do 03.2016 (87 obserwacji) miał minimum na poziomie -40%, a maksimum prawie +54%. Poniżej jest wykres oszacowanego rozkładu sWIG80 (zrobiony w Gretlu za pomocą jądra Gaussa - metoda ta daje zniekształcony obraz, bo sugeruje, że wystąpiły wartości poniżej -40%, co jest nieprawdą):

W tym wypadku lepszy okazuje się rozkład normalny, choć występuje tu pewna prawostronna skośność.

Duan [1] przedstawił metodę retransformacji, która nie zakłada z góry żadnego rozkładu. Duan nazwał swój estymator "smarującym estymatorem" (smearing estimate). Pokazał, że jego estymator daje lepsze rezultaty, tzn. jest bardziej efektywny, gdy rozkład stopy zwrotu nie jest log-normalny, a więc gdy logarytmiczna stopa zwrotu nie posiada rozkładu Gaussa. 

Smarujący estymator (SE) dla oczekiwanej stopy zwrotu można zapisać następująco:

(3)

Wariancja składnika losowego jest tym razem stała w czasie, czyli występuje jednocześnie  homoskedastyczność i stacjonarność składnika losowego. Składnik losowy jest tutaj różnicą pomiędzy sąsiadującymi składnikami losowymi modelu logarytmicznej ceny, dlatego że pierwotny składnik losowy w modelu (1) jest niestacjonarny (porównaj zapis wariancji w obu przypadkach). Oczekiwana stopa zwrotu powstała po prostu przez zapis:

Nic więc dziwnego, że aproksymacją będzie:

(4)

Korekta Duana to zwykła średnia arytmetyczna kolejnych stosunków reszt z regresji liniowej. 

Gdy rozkład log-stopy jest normalny i znamy pełną populację to (4) sprowadza się do:

oraz gdy jest normalny i nie znamy pełnej populacji, to z modelu (2) wynika, że:

Model (3) można więc traktować jako uogólnienie (2). Trzeba jednak zaznaczyć, że oryginalny wzór Duana jest nieco bardziej ogólny niż ten, który podałem w (3): w naszym przypadku rolę zmiennej objaśniającej pełni zmienna czasowa, która się redukuje, natomiast w oryginale jest zastąpiona zmienną x, która może być dowolna (wtedy też w modelu (3) ocena parametru b z falką będzie przemnożona dodatkowo przez x).

Model (3) pozwala też zrozumieć zależności pomiędzy średnią warunkową a niewarunkową. Jeżeli nie istnieje liniowa korelacja między okresem T a logarytmiczną ceną ln(P), czyli gdy ocena b = 0 w modelu (1), to oczekiwana stopa zwrotu w (3) sprowadza się do zwykłej średniej arytmetycznej:

Przykład.

Aby porównać model (2) z (3), użyję tych samych danych co poprzednim razem, tj. dla mbanku - rocznie 1994-2015 (22 obserwacje). Nie będę się wgłębiał w to czy stopy mbanku są normalne, lognormalne czy jeszcze inne. Zaczynamy od zlogarytmowanego modelu (1):

Parametr b wyniósł 11,18%. Korzystając z Gretla uzyskałem reszty powyższej regresji liniowej, które podstawiłem do wzoru (4), czyli korekty SE. Korekta ta wyniosła 1,0699. Podstawmy to do (3):

Dla porównania stosując model (2) uzyskałem wielkość 18.69%, natomiast dla standardowego wzoru na wartość oczekiwaną w rozkładzie lognormalnym (czyli dla k = 0) 18.73%. Dodatkowo przypomnę, że średnia arytmetyczna wyniosła 20,08%, a geometryczna 11,71%. Pamiętać trzeba, że geometryczna średnia dotyczy tylko inwestycji długoterminowej, dlatego SE staje się konkurencyjny głównie w stosunku do średniej arytmetycznej (która będzie poprawna w sytuacji, gdy logarytmiczna cena nie jest liniowo skorelowana z okresem czasu) oraz do estymatora z (2) (który jest poprawny dla próby w rozkładzie log-normalnym).

Literatura:

[1] N. Duan, Smearing Estimate: A Nonparametric Retransformation Method, Sep. 1983